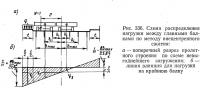
1. Определение расчетных усилий в главных балках
Пролетное строение представляет собой пространственную конструкцию, образуемую балками, связями, а в автодорожных мостах и, в ряде случаев, железнодорожных, также железобетонной или ребристой стальной плитой проезжей части.
Ввиду значительной сложности учета действительных условий работы пролетного строения как пространственной конструкции, в практике проектирования получили широкое распространение приближенные методы учета распределения нагрузки между главными балками.
Характер распределения усилий между частями пространственной конструкции зависит от степени жесткости элементов и их соединений.
При отсутствии промежуточных поперечных связей или. значительной их податливости, которая позволяет не учитывать их влияния, распределение временной вертикальной нагрузки между главными балками выражается законом рычага.
При жестких поперечных связях, деформации которых незначительны по сравнению с прогибами главных балок, можно пренебречь искривлениями поперечных сечений пролетных строений под временной вертикальной нагрузкой, несимметрично расположенной поперек моста и принимать распределение этой нагрузки между главными балками по методу «внецентренного сжатия».
При балках одинакового сечения, рассматривая воображаемый стержень, материал которого сконцентрирован в нескольких фибрах, число и размещение которых соответствуют числу и размещению главных балок, и полагая условно площадь каждой фибры, а также величину нагрузки N, равными 1, формулу для напряжений при внецентренном сжатии можно привести к виду:
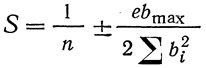
где S — доля нагрузки N = 1, приходящаяся на крайнюю балку; n — число главных балок, е, bi и bmax — размеры, указанные на рис. 336, a.
Индекс i изменяется от единицы до числа главных балок, находящихся но одну сторону от оси моста.
Нетрудно видеть, что график (рис. 336, б) является линией влияния для нагрузки на крайнюю балку. Загружая положительную площадь линии влияния временной вертикальной нагрузкой на проезжей части и на тротуаре, можно вычислить коэффициент поперечной установки для крайней балки по формуле:
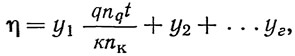
где qnqt/knk — коэффициент приведения нагрузки тротуара к нагрузке проезда, y1 — ордината линии влияния под осью тротуара; y2...yi — то же, под осями автомобилей; q — интенсивность нагрузки тротуара, т/м2; t — ширина тротуара, м; к — эквивалентная временная вертикальная нагрузка проезжей части, т/м; nq, nk — коэффициенты перегрузки для нагрузки тротуаров и проезда.
Метод внецентренного сжатия широко используется при проектировании металлических автодорожных мостов.
Для мостов под однопутную железную дорогу е = О, т. е. временная вертикальная нагрузка распределяется между главными балками поровну.
При широких пролетных строениях и относительно небольших пролетах прогибы главных балок соизмеримы с деформациями поперечных связей и пролетное строение в поперечном разрезе заметно искривляется. Метод внецентренного сжатия становится грубо приближенным, особенно при определении расчетных усилий в сечениях балок, близко расположенных к опорам.
Методы рычага и внецентренного сжатия малопригодны также для получивших широкое распространение конструкций пролетных строений с широкими коробчатыми (замкнутого профиля) балками, горизонтальные плиты которых принимают значительное участие в работе пролетных строений на кручение.
Возникла необходимость в разработке новых методов пространственного расчета пролетных строений, с использованием расчетных схем, отражающих действительные условия их работы.
Теоретические основы такого расчета создавались рядом советских и зарубежных ученых таких, как С. Г. Галеркин, П. Ф. Папкович, В. 3. Власов, С. П. Тимошенко, А. А. Уманский, Б. Е. Улицкий, В. Г. Донченко, Г. Ромберг, Гюйон и др.
Расчет пролетных строений с неразрезными балками дополнительно осложняется статической неопределимостью балок.
Расчет неразрезных балок можно производить по линиям влияния, для вычисления ординат которых рядом автором составлены таблицы. Заметим, что расчет неразрезных балок возможен и без вычисления площадей линий влияния, так как для определения невыгоднейшего положения временной нагрузки на балке при вычислении расчетного усилия в каком-либо ее сечении достаточно знать форму линии влияния, которая может быть получена, без каких-либо вычислений, как кинематическая модель линии влияния, а опорные моменты при заданном загружении могут быть вычислены простым и удобным итерационным методом уравновешивания опорных моментов1.
2. Подбор сечений
При подборе сечений балок важное значение имеет правильный выбор их высоты. От высоты балок зависят вес и вертикальная жесткость пролетного строения, условия его изготовления, перевозки и монтажа.
Во многих случаях при езде поверху от высоты балок зависит высота насыпи на подходах к мосту, а следовательно, и стоимость этих подходов.
Так как при работе балки на изгиб материал ее наиболее полно используется в поясах и значительно меньше у нейтральной оси, то при подборе сечения балки выгодно стенку принимать высокой и тонкой, размещая материал главным образом в поясах.
Минимально допустимая толщина стенок клепаных балок 10 мм; сварных главных балок — 12 мм. Ограничения эти вызваны стремлением замедлить ощутимое ослабление листов коррозией, а для сварных балок, кроме того, уменьшить сварочные деформации.
При заданном расчетном изгибающем моменте М площадь поперечного сечения балки F и, следовательно, ее теоретический вес можно представить в виде функции от высоты балки h и толщины ее стенки δ. Можно найти минимум этой функции, приравняв нулю производную dF/dH. В результате получим с учетом толщины поясного пакета δп:
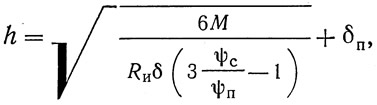
где ψс и ψп — конструктивные коэффициенты стенки и поясов; ψс/ψп = 0,9÷1,3.
Минимальное значение отношения ψс/ψп соответствует сварным балкам небольших пролетов; максимальное — клепаным балкам значительных пролетов.
Найденная высота будет высотой балки минимального веса.
Однако не следует преувеличивать значение принципа минимизации веса балки, так как с выбором ее высоты связан, кроме веса, ряд других, технико-экономических показателей пролетного строения, упомянутых выше.
Во многих случаях высоту балок назначают меньше оптимальной по условиям веса, стремясь уменьшить строительную высоту пролетного строения или облегчить условия его изготовления, перевозки и монтажа.
Минимально допустимая высота балок определяется требованиями вертикальной жесткости пролетного строения.
Для разрезной балки эта высота может быть приближенно определена по формуле:
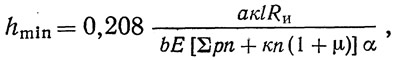
где α≈1,1 — коэффициент, учитывающий изменение сечения балки по ее длине; к — временная вертикальная нормативная статическая погонная нагрузка; l — пролет балки; b=δ/l — предельное нормативное отношение прогиба балки к пролету; ∑p — погонная нормативная постоянная нагрузка; α=Iбр/Iн — отношение момента инерции брутто балки в середине пролета к моменту инерции нетто.
Для клепаных балок его можно принять равным 1,17; для сварных — 1. Остальные обозначения общепринятые.
В существующих автодорожных мостах с разрезными главными балками, имеющими сплошные стенки, отношение высоты балок к пролету колеблется в пределах 1/12—1/20.
При одинаковых пролетах и нагрузках неразрезные балки жестче разрезных вследствие наличия отрицательных опорных моментов. Расчетный прогиб неразрезной балки в рассматриваемом пролете, приближенно полагая момент инерции балки в этом пролете постоянным, можно определить по формуле:
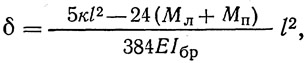
где к — нормативная статическая временная вертикальная нагрузка; Мл и Мп — опорные моменты на левом и правом концах рассматриваемого пролета, соответствующих невыгоднейшему загружению для этого пролета нагрузкой к.
Соответственно повышенной жесткости неразрезных балок минимально допустимая высота их в серединах пролетов может быть уменьшена по сравнению с разрезными балками.
Серьезное значение имеет выбор формы поперечного сечения и размеров поясов главных балок. Балкам, не работающим совместно с железобетонной или стальной плитой, придается, как правило, симметричное двутавровое сечение.
Размеры поясных уголков в клепаных балках должны быть связаны с мощностью пакетов горизонтальных листов, прикрепляемых уголками к стенке.
Толщина пакета горизонтальных листов, включая полки поясных уголков и накладки в стыках, не должна быть более 4,5 диаметра заклепочного отверстия, а число склепываемых тел в пакете не должно превышать 7 при диаметре заклепок 23 мм и 8 — при диаметре заклепок 26 мм.
При клепке в два пневматических молотка, один из которых заменяет поддержку, или же на скобе толщина пакета может быть увеличена до 5,5 диаметра, а число склепываемых тел увеличено до 8 при заклепках d=23 мм и до 9 при заклепках d=26 мм (ТУ, п. 480).
Толщина 6 поясных листов сварных балок из углеродистой стали не должна быть больше 50 мм, а из низколегированной стали — 40 мм (ТУ, п. 460).
Ширина неокаймленного свеса сжатого пояса сварных балок с ездой поверху не должна превышать в железнодорожных мостах 10 6 и 0,3 м; в автодорожных и городских мостах — 15 δ и 0,4 м (ТУ, п. 463). Здесь δ — толщина пояса.
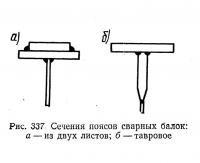
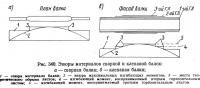
Если предельные толщина и ширина одиночного листа пояса не обеспечивают необходимую площадь пояса, а увеличение высоты балки нежелательно, можно использовать одну из показанных на рис. 337 форм пояса.
Площадь поясных уголков, прикрепляющих к стенке горизонтальные листы, должна соответствовать площади последних, составляя, примерно 30% всей площади пояса.
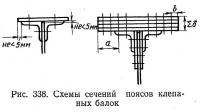
Когда зту рекомендацию в случаях мощных балок трудно реализовать из-за ограниченности сортамента уголкового проката, можно часть необходимой площади балки разместить в виде вертикальных листов (ламелей) между стенкой балки и поясными уголками (рис. 338) или перейти к двухстенчатым балкам.
Ширина верхних поясов продольных и главных балок железнодорожных мостов с ездой на деревянных поперечинах по условиям работы поперечин на смятие должна быть не меньше 240 мм.
Ширина свеса α поясного пакета листов клепаных балок, считая от наружного ряда заклепок поясных уголков до кромок листов из углеродистой стали, должна быть не больше 12 ∑δ, где ∑δ — толщина пакета. При листах из низколегированной стали α должна быть не больше 10 ∑δ.
Для обеспечения плотности пакета листов пояса расстояние b от края пакета до ближайшего ряда заклейок должно быть не больше 120 мм и 8δ, где δ — толщина наиболее тонкого листа пакета.
Толщина листов в клепаных балках должна быть не более 20 мм по условиям прокалывания отверстий на дыропробивных станках.
Удачно подобранное сечение балки должно удовлетворять требованиям прочности, выносливости, технологичности (удобствам изготовления и монтажа) и в конечном счете экономичности по затратам материала и труда при обеспеченной надежности в эксплуатации. Проверки прочности производятся по величинам:
а) нормальных краевых напряжений

б) касательных напряжений у нейтральной оси балки, в сечениях наибольших значений перерезывающей силы Q
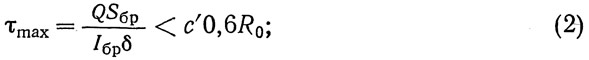
в) приведенных напряжений
В этих формулах:
Wн — момент сопротивления балки нетто в проверяемом сечении. Если балка несимметрична относительно горизонтальной оси, то момент сопротивления для определения максимальных напряжений нужно вычислить для волокна балки, более удаленного от центра тяжести проверяемого сечения; Rи и R0 — расчетные сопротивления стали по табл. ТУ, п. 383; Sбр — статический момент брутто относительно нейтральной оси любой части сечения, расположенной по одну сторону от нейтральной оси; Iбр — момент инерции сечения брутто; δ — толщина стенки балки; с' — коэффициент увеличения расчетного сопротивления сдвигу, учитывающий неравномерное распределение касательных напряжений в стенке балки:

где Н — полная высота стенки.
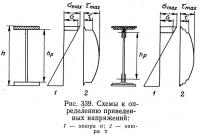
Нормальное σ и касательное τ напряжения в формуле (3) должны быть вычислены в точках, где приведенные напряжения достигают максимума. По длине балок эти точки находятся в сечениях, где достигают больших значений одновременно и М, и Q. Такими сечениями являются, например, сечения неразрезных и консольных балок над промежуточными опорами. По высоте сечений максимальные значения находятся на уровнях прикреплений поясов к стенке (рис. 339).
Нормальное и касательное напряжения в этих точках могут быть вычислены по формулам:
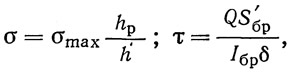
здесь h — полная высота балки; hр — для сварной балки — полная высота стенки; для клепаной балки — расстояние между рисками поясных уголков; S'бр —статический момент брутто относительно нейтральной оси: для сварной балки — горизонтального листа; для клепаной балки — горизонтальных листов, поясных уголков и части стенки между риской поясных уголков и горизонтальными листами (на рис. 339 заштриховано).
Значения расчетных изгибающих моментов по длине балки изменяются. Подбор сечения балки производится, в первую очередь, в сечении с максимальным изгибающим моментом. По мере уменьшения изгибающих моментов, сечения балки уменьшают за счет, главным образом, площади поясов.
В сварных балках уменьшают толщину и ширину горизонтальных листов; в клепаных балках — число листов в поясных пакетах. Возможность такого уменьшения должна быть предусмотрена при подборе сечения балки в месте максимального изгибающего момента, где пояса должны быть достаточно мощными.
Сечения балки, начиная с которых площадь их может быть безопасно уменьшена, определяют обычно графически, при помощи эпюры материалов (рис. 340).
Поверки выносливости балки выполняются только по нормальным напряжениям по формуле:

Здесь γ — коэффициент понижения расчетного сопротивления, учитывающий явление усталости материала.
Для основного металла элементов конструкции, испытывающих преимущественное растяжение σmax>0, а также для соединения на заклепках и на болтах при любом знаке σmax коэффициент γ определяется по формуле:
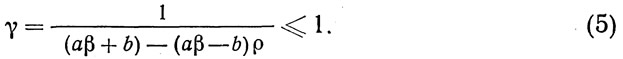
При преимущественном сжатии основного металла (σmax<0):
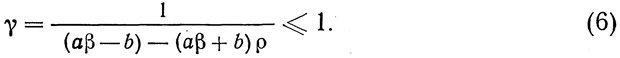
В формулах для γ:
β — эффективный коэффициент концентрации напряжений, учитывающий влияние на выносливость различных условий концентраций напряжений. Таблица коэффициентов дана в приложении 16 к ТУ; ρ=σmin/σmax — характеристика цикла переменных напряжений; sigma;max, sigma;min — наибольшее и наименьшее по абсолютной величине значения напряжений со своими знаками (плюс — для растяжения, минус — для сжатия);
при F=1, m2=1 и с=1 — n=μ
Таким образом, μ представляет собой число болтов, необходимых для прикрепления или соединения в стыке единичной площади, при m2=1 и с=1.
Значения коэффициента μ приведены в табл. 13.
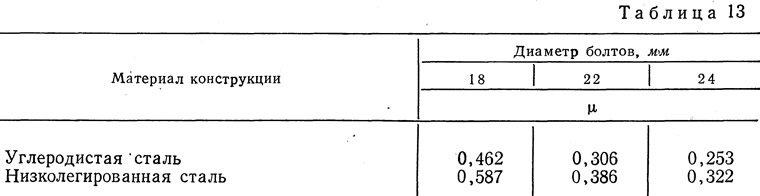
Табличные значения коэффициентов μ соответствуют расчетному сопротивлению болта при одной контактной площадке трения, например, при нахлесточном соединении (рис. 341, а). При двух площадках трения (рис. 341,6) уменьшается в 2 раза. В соединении на рис. 341, в число площадок трения равно 4 и коэффициент μ для этого случая нужно уменьшить в 4 раза по сравнению с табличным значением.
Коэффициент условий работы m2 принимается равным 0,9 в случаях, когда:
а) число болтов в соединении меньше 5;
б) число тел, образующих пакет в соединении, больше 6.
В прочих случаях осевого действия усилия S коэффициент можно принять равным единице.
При расчете совмещенных стыковых соединений количество болтов в полунакладке, определенное по формулам (7) или (8), нужно увеличить на 0,5 n', где n' — число болтов в крайнем ряду у центра стыка, так как расчетное сопротивление этих болтов учитывается в размере 50% от нормативного (ВСН 144-68, п. 4.12).
Особенностью соединений на фрикционных болтах является начало передачи усилия 5 в окрестности ослабленного сечения (рис. 341, г). Поэтому расчет соединяемых элементов на прочность производят по сечению нетто в предположении, что 40% усилия, приходящегося на каждый болт в рассматриваемом сечении, уже передано силами трения (ВСН 144-68, п. 4.4). С учетом этого указания усилие в сечении нетто по первому поперечному ряду болтов в соединении будет:
где n'' — число болтов в проверяемом сечении.
Чтобы привести формулу проверки прочности соединяемых элементов к обычному виду:
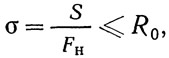
нужно умножить действительную площадь нетто проверяемого сечения на коэффициент, равный:
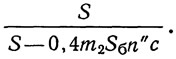
Прочность стыковых накладок проверяется на полное усилие по действительной площади Fн.
Расчет соединяемых элементов на выносливость и устойчивость производят по сечению брутто.
При соединениях на заклепках количество последних может быть определено по приведенной выше формуле (8), причем значения коэффициентов μ даны в табл. 14.
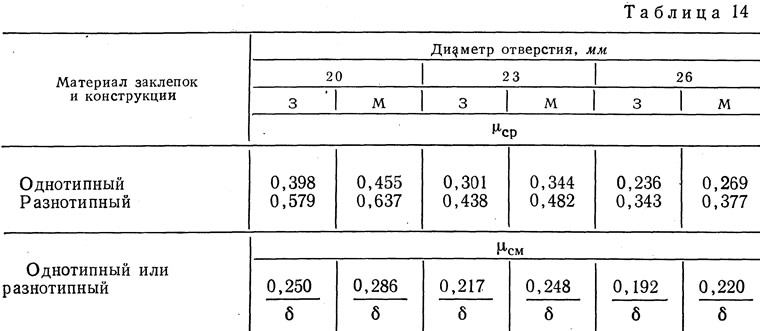
Для заклепок, работающих на двойной срез, коэффициенты нужно уменьшить в 2 раза.
δ — в знаменателе величины μсм — толщина более тонкого из соединяемых элементов.
4. Расчет прикрепления пояса балки к стенке
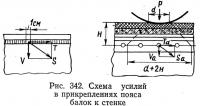
Расчет ведется на прочность и на выносливость при действии сдвигающих усилий; горизонтального Т, возникающего при изгибе балки между стенкой и поясом (рис. 342), и вертикального V от временной вертикальной нагрузки, если эта нагрузка передается на пояс балки через мостовые поперечины или железобетонную плиту.
Эти усилия на 1 см длины балки будут:
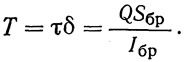
Здесь Sбр — статический момент брутто площади пояса относительно нейтральной оси балки; Q — максимальная поперечная сила на участке балки, где толщина поясных швов или шаг поясных заклепок сохраняются постоянными.
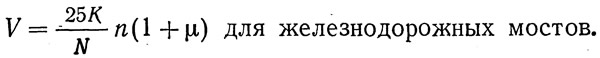
Здесь 25 К кГ/см пути — местное давление временной вертикальной нагрузки класса К, передаваемое мостовой поперечиной. При передаче нагрузки железобетонной плитой это давление принимается равным 20 К кГ/см пути. N — число стенок балок на один путь; n=1,29 и (1+μ)=1,545 — коэффициенты перегрузки и динамический, соответствующие минимальной длине загружения λ=3 м (ТУ, п. 126).
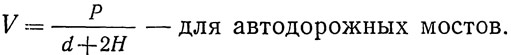
Здесь Р — давление колеса подвижной нагрузки, распределенное в уровне верха дорожного покрытия, на нормативную длину (ТУ, приложение 10, табл. 1) вдоль пролета балки, кГ; Н — расстояние от поверхности дорожного покрытия до уровня действия усилия T; n — коэффициент перегрузки (1,4 — для автомобилей и 1,1 — для НК-80); 1+μ — динамический коэффициент, вычисленный при λ=d+2Н для автомобильной нагрузки, и равный единице для нагрузки НК-80.
Равнодействующая S усилий Т и V на 1 см длины балки:
на длину шага поясных заклепок:
Сопротивление сварных швов на 1 см длины балки:
Здесь h — размер катета углового шва при автоматической сварке; n — число швов, прикрепляющих пояс к стенке.
Необходимый из условия прочности размер катета углового шва:
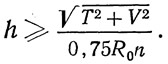
Наименьший допустимый размер катета углового шва ограничен требованиями ТУ (см. табл. 53 к п. 485).
Сопротивление одной поясной заклепки диаметром d смятию:
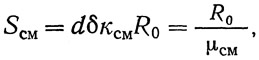
где δ — толщина стенки балки.
То же, двойному срезу:
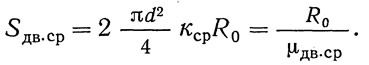
Здесь ксм и кср — коэффициенты перехода от основного расчетного сопротивления R0 к сопротивлению материала заклепки смятию и срезу (ТУ, п. 384, табл. 38);
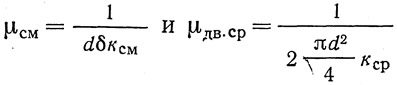
— коэффициенты сопротивления заклепки смятию и двойному срезу.
Максимальный из условия прочности шаг поясных заклепок:
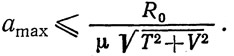
Здесь μ — наибольший из коэффициентов μсм и μдв.ср.
5. Размещение ребер жесткости
Поперечные ребра жесткости должны быть установлены над опорами и в местах передачи сосредоточенных сил.
Установкой указанных ребер можно ограничиться без проверки расчетом местной устойчивости, если толщина стенки изгибаемой балки не менее 1/50 h, где h — расчетная высота стенки, равная при сварной конструкции — полной высоте стенки, при клепаной конструкции — расстоянию между ближайшими к оси стенки рисками поясных уголков.
При толщине стенки из углеродистой стали менее 1/50 h, помимо указанных выше ребер жесткости, устанавливаются дополнительно промежуточные поперечные ребра жесткости.
Максимально допустимые расстояния между смежными поперечными ребрами жесткости уточняются расчетом местной устойчивости.
Высокие балки с тонкими стенками укрепляются также продольными ребрами жесткости. При установке одного продольного ребра расстояние его от сжатого пояса рекомендуется назначать равным (0,20—0,25) h.
В случае установки двух или трех продольных ребер жесткости первое ребро рекомендуется размещать на расстоянии (0,15—0,20) h, а второе ребро — на расстоянии (0,40—0,50) h от сжатого пояса. Третье ребро размещают обычно в растянутой зоне стенки для увеличения критического касательного напряжения.
Ширина выступающей части парного симметричного ребра при наличии одних поперечных ребер жесткости должна быть с каждой стороны стенки не менее h/30 + 40 мм, где h в мм.
При одновременной установке поперечных и продольных ребер жесткости размеры их подбираются так, чтобы моменты инерции сечений ребер удовлетворяли условиям:
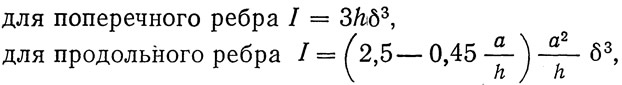
но не менее 1,5hδ3 и не более 7hδ3, где α — расстояние между поперечными ребрами жесткости.
Когда ребра располагают с одной стороны стенки, момент инерции вычисляют относительно оси, совпадающей с ближайшей к ребру гранью стенки. Толщина ребра должна быть не менее 1/15 ширины выступа и не менее 10 мм.
При отсутствии горизонтального листа в верхнем поясе клепаной балки и опирании на этот пояс мостовых брусьев выступающие части поперечных ребер жесткости должны быть пригнаны к горизонтальным полкам поясных уголков.
6. Расчет опорных ребер
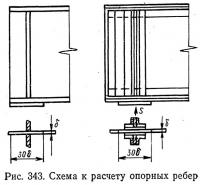
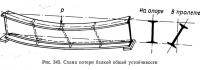
Опорные ребра, воспринимающие нижними торцами опорные реакции 5 (рис. 343) и передающие их стенке по высоте балки, должны быть проверены на устойчивость из плоскости балки, на смятие торцов и по прикреплению их к балке.
При проверке устойчивости опорные ребра рассматриваются условно как сжатая силой S стойка, в сечение которой, кроме самих ребер, включается стенка балки в виде вертикальной полосы, шириной 30δ, где δ — толщина стенки. Свободная длина стойки принимается равной 0,7 расстояния (по вертикали) между узлами опорных, поперечных связей.
Условие устойчивости:
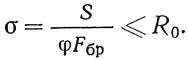
Проверка на смятие торцов ребер производится по формуле:
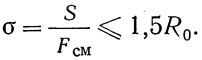
Здесь Fсм — площадь торцов опорных ребер в сварной балке или площадь торцов выступающих полок уголков и зажатых между ними полос (если они имеются) в клепаной балке. На рис. 343 эта площадь заштрихована.
Заклепки или сварные швы при проверке прикрепления ребер жесткости рассчитываются условно на полное усилие S.
7. Расчет стыков балок
Стыки балок можно рассчитывать по величине расчетных усилий (момента М, поперечной и продольной сил Q и N), действующих в сечении стыка или исходя из принципа равнопрочности балки в стыке и сечении рядом со стыком. Во втором случае можно и не знать величины расчетных усилий в сечении стыка, достаточно знать размеры сечения балки.
Независимо от способа расчета стык конструируется так, чтобы каждый элемент сечения балки (стенка, горизонтальные листы, поясные уголки) имел в стыке самостоятельное перекрытие.
Рассмотрим расчет стыка по расчетным усилиям. При расчете стыка вертикального листа предполагается, что от действия изгибающего момента усилия между болтами распределяются, как в материале стенки, пропорционально удаленности болтов от горизонтальной оси, проходящей через центр тяжести болтов стыка (в балках симметричного профиля эта ось совпадает, как правило, с нейтральной осью балки).
Предполагается далее, что поперечная сила распределяется между болтами стенки, а продольная сила между всеми болтами по каждую сторону стыка — поровну.
Усилие в болтах крайнего горизонтального ряда от действия изгибающего момента М, приходящегося на стенку балки, будет равно:
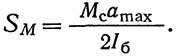
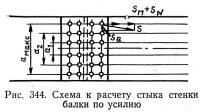
Момент Мс равен расчетному моменту М в сечении стыка, умноженному на отношение момента инерции нетто стенки к моменту инерции нетто всего сечения; расстояние от крайнего горизонтального ряда болтов до центра тяжести болтов стыка (рис. 344);
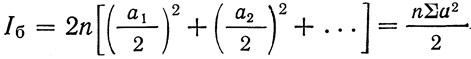
— момент инерции болтов, поставленных в пределах полунакладки; n — число вертикальных рядов болтов в полунакладке (на рис. 344 n=2)
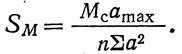
Усилие на каждый болт от действия поперечной силы:
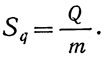
То же, от действия продольной силы:
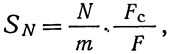
где m — число болтов в полунакладке; Fс и F — площади нетто стенки и всего сечения балки.
Полное усилие на один болт крайнего ряда:
Это усилие не должно превосходить несущей способности болта:
Здесь 2 — число площадок трения при двусторонних накладках.
Расчетными усилиями от изгибающего момента для стыков горизонтальных листов и поясных уголков являются продольные осевые усилия, которые могут быть вычислены путем деления изгибающих моментов, приходящихся на долю указанных элементов сечения, на плечи этих моментов, равные расстояниям между центрами тяжести одноименных элементов верхнего и нижнего поясов. Так, например, расчетное усилие, приходящееся на оба поясных уголка каждого пояса балки, будет:
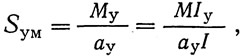
где My — доля изгибающего момента, приходящаяся на поясные уголки; αy — расстояние между осями уголков верхнего и нижнего поясов; Iу — момент инерции поясных уголков нетто.
Усилие, передающееся на один болт с пары уголков,
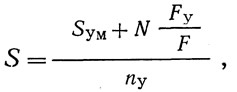
где ny — число болтов в уголковой полунакладке; Fy — площадь нетто уголков.
При устройстве стыка на заклепках расчет ведется аналогично, но при проверке прочности вместо расчетного сопротивления болта нужно подставить в поверочную формулу расчетное сопротивление заклепки R0/μ двойному срезу или смятию в зависимости от того, какое из этих сопротивлений меньше.
8. Проверка общей устойчивости балки
Под общей устойчивостью балки, загруженной силами, действующими в ее плоскости, подразумевается сопротивляемость балки скручиванию (рис. 345), которое возникает при возрастании нагрузки до критического значения, зависящего от размеров поперечного сечения балки, расстояния между узлами связей сжатого пояса и модуля упругости балки. При расстоянии между узлами продольных связей, не превышающем 15-кратной ширины сжатого пояса балки, общую устойчивость ее можно считать обеспеченной.
При несоблюдении указанного соотношения нужно проверить общую устойчивость балки. Условная проверка этой устойчивости может быть выполнена, как проверка центрально сжатого стержня, имеющего форму и размеры поперечного сечения сжатого пояса балки и свободную длину, равную расстоянию между узлами продольных связей. Условный стержень проверяется на устойчивость из плоскости балки по формуле:
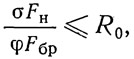
где σ — напряжение в центре пояса в середине его свободной длины; Fн и Fбр — площадь нетто и брутто пояса балки, в которую включаются: при сварных балках — горизонтальный лист; при клепаных балках — горизонтальные листы, поясные уголки и часть стенки в пределах уголков.
9. Проверка местной устойчивости стенки балок
Местная устойчивость стенки балки зависит от величины нормальных и касательных напряжений, действующих в ней, от соотношения таких размеров, как толщина стенки и длины сторон отсеков (участков стенки, ограниченных поясами и ребрами жесткости) и от степени защемления сторон отсека.
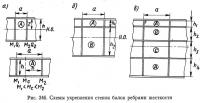
Проверка местной устойчивости стенки, укрепленной только вертикальными ребрами (рис. 346, а), производится по формуле:

Значения изгибающих моментов и поперечных сил берутся из расчетов на прочность.
σ0, τ0, ρ0 — критические значения напряжений σ, τ и ρ, при которых стенка балки теряет устойчивость. Формулы и таблицы для определения этих напряжений, а также соответствующих критических напряжений для случаев укрепления стенки балки ребрами жесткости (рис. 346,6, в) приведены в ТУ (приложение 18); m — коэффициент условий работы, принимаемый равным 0,9 для сварных балок (с учетом начальных искривлений стенки под влиянием сварочных напряжений) и 1,0 — для клепаных балок. Эти значения m сохраняются и для случаев укрепления стенки балки ребрами жесткости (см. рис. 346, б, б).
При укреплении стенки балки, помимо вертикальных ребер жесткости, одним горизонтальным ребром (рис. 346,6), расположенным в сжатой Зоне балки, устойчивость отсека стенки A, примыкающего к сжатому поясу, проверяется по формуле:
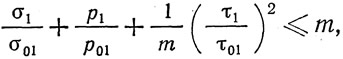
а отсека, примыкающего к растянутому поясу и находящегося частично в сжатой, частично в растянутой зоне, по формуле:
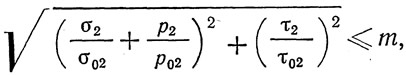
которая тождественна по структуре формуле для случая балки с одними вертикальными ребрами (рис. 346, а). М и Q, вводимые в расчет для определения напряжений σ1, σ2, τ1 и τ2, вычисляют так же, как в схеме α.
Напряжения σ1 и σ2 по краям отсеков А и В со стороны сжатого пояса и касательные напряжения τ' и τ''' по краям стенки и τ'' по оси продольного ребра, вычисляются по соответствующим формулам сопротивления материалов, причем:
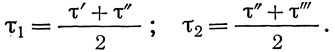
Напряжение р для отсека А вычисляют, как в схеме α; для отсека В — по формуле:
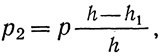
т. е. принимают убывающим по высоте стенки по линейному закону от величины p до нуля.
При укреплении стенки балки вертикальными и несколькими горизонтальными ребрами жесткости (см. рис. 346, в) устойчивость стенки в отсеках А и В проверяется так же, как отсека А (см. рис. 346,6), а в отсеке С так же, как в отсеке В (см. рис. 346, б).
Устойчивость стенки в отсеке Д, находящемся полностью в растянутой зоне, проверяется по формуле:
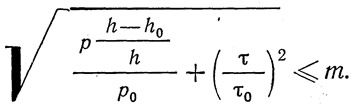
Касательное напряжение τ так же, как по рис. 346, б, определяется как полусумма касательных напряжений по оси нижнего горизонтального ребра и по нижнему краю стенки.
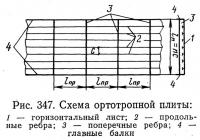
10. Расчет ортотропных плит
Ортотропная плита проезжей части состоит из стального горизонтального листа, приваренных к ней продольных и поперечных ребер.
Горизонтальный лист и продольные ребра плиты включаются в состав поясов главных балок и рассчитываются, как на местную нагрузку, так и на нагрузку главных балок. При назначении минимальной толщины вертикального листа необходимо учитывать не только его прочность, но также и трещиностойкость асфальтобетонного дорожного покрытия.
Опыт эксплуатации показывает, что трещиностойкость асфальтобетонного покрытия автодорожных мостов обеспечивается при следующих соотношениях расстояний с между продольными ребрами и толщиной листа δ:
| c | δ |
| 250 мм | 10 мм |
| 300 мм | 12 мм |
| 350 мм | 14 мм |
Расстояние между осями одностенчатых продольных ребер назначают часто равным 300 мм. При ребрах (закрытого профиля трапецеидальной, и-образной или v-образной формы) указанное расстояние назначают в свету между ребрами.
Расстояние между поперечными ребрами принимают: при одностенчатых ребрах 1,8—2,5 м, при ребрах и-образной формы — 2,5—4,0 м.
Высоту продольных ребер принимают в пределах 1/15—1/20 пролета; поперечных — 1/8—1/12 пролета.
При подсчете моментов инерции ребер в состав их сечения включают полосу листа. Ширину полосы, включаемой в состав продольных ребер, принимают равной расстоянию между осями ребер. Ширину полосы, включаемой в состав поперечных ребер, принимают равной 1/5 пролета этих ребер.
Иногда для упрощения технологии изготовления плиты продольные ребра не пропускают в прорези в стенке поперечных ребер, а опирают на них сверху. При таком этажном расположении ребер лист в работе поперечных ребер не участвует.
Пространственный расчет стальной ребристой плиты весьма трудоемок, даже при использовании ЭЦВМ. Имеются предложения выполнять расчет ребристой плиты, как эквивалентной по жесткости безреберной (континуальной) ортотропной плиты, методами теории упругости.
При назначении размеров конструкции в первом приближении используются простейшие способы.
При этом предполагается, что давление колес местной нагрузки передается на расчлененные друг от друга продольные полосы плиты шириной b+2H, в состав которой входят n ребер, причем:
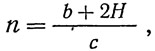
где b — ширина обода колеса; Н — толщина дорожного покрытия.
Изгибающий момент в середине пролета расчетной полосы, непрерывно проходящей над промежуточными опорами в виде поперечных ребер или балок, можно принять:
где М0 — изгибающий момент в середине пролета разрезной балки пролетом lпр (рис. 347).
Опорный момент Моп можно принять равным 0,6 М0.
Напряжения в плите, полученные расчетом на местную нагрузку, нужно просуммировать с напряжениями в плите как в верхнем поясе главных балок. В состав этого пояса включают горизонтальный лист и продольные ребра, которые должны иметь стыки, проверенные на прочность по изгибающему моменту в плите и в главных балках. Если главные балки, входящие в состав комбинированной системы, испытывают продольные усилия, то должны быть учтены и эти усилия.
При приближенном расчете плиты, как пояса главных балок, предполагается, что напряжения в ней равномерно распределены по ширине плиты. В действительности напряжения у стенок главных балок несколько выше, чем в удалении от них, причем неравномерность распределения напряжений тем значительнее, чем меньше вертикальная жесткость продольных ребер.
Если ортотропная плита попадает в зону отрицательных изгибающих моментов в главных балках (в неразрезных и комбинированных пролетных строениях), то нижние пояса сжатых одностенчатых продольных ребер должны быть проверены на устойчивость формы.
Нижняя полка продольного ребра работает на продольное сжатие в условиях стержня в упругой среде вследствие защемления стенки ребра в горизонтальном листе плиты. Сопротивление упругой среды характеризуется усилием, которое нужно приложить к каждому погонному сантиметру полки, чтобы вызвать ее смещение в горизонтальной плоскости на 1 см. Это усилие выражается равенством:

Задачу устойчивости сжатого стержня в упругой среде можно свести к задаче устойчивости свободного стержня путем замены действительной длины стержня l приведенной длиной lприв путем умножения l на коэффициент α, меньший единицы. В работе С. П. Тимошенко2 дана таблица значений α в зависимости от β и I (табл. 15), причем I в данном случае момент инерции (в см4) полки продольного ребра на 1 см ее длины относительно нейтральной плоскости, перпендикулярной к плоскости полки. Этот момент инерции равен δпd3/12, где δп и d — толщина и ширина полки (в см).
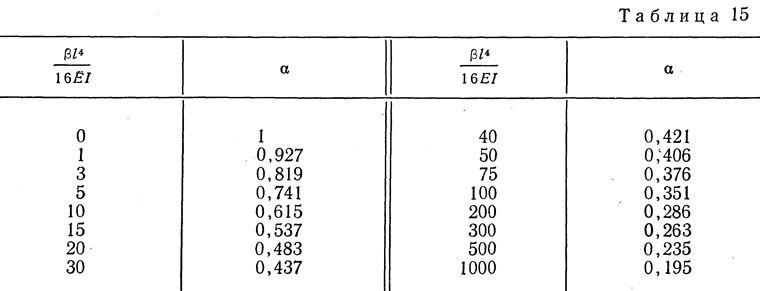
Гибкость полки ребра в ее плоскости будет:
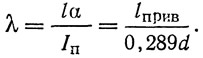
Остается по λ определить φ и проверить выполнение условия устойчивости:
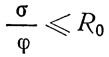
(σ — полные расчетные напряжения сжатия в полке продольного ребра).
Расчетные усилия и напряжения в поперечной балке от местной нагрузки определяются обычным способом.
Примечания
1. Кани Г. Расчет многоэтажных рам. М., Госуд. изд-во литературы по строительству, архитектуре и строительным материалам, 1963.
2. Тимошенко С. П. Устойчивость упругих систем. М., Огиз-Гостехиздат, 1946.