Проектирование и расчет пневматических сооружений

Воздухоопорные пневматические сооружения обладают многими преимуществами по сравнению с обычными конструкциями. Они представляют собой весьма эффективные конструктивные системы, в особенности для сооружений с большими пролетами без промежуточных опор.

Пневматические конструкции часто применяются как временные или сезонные сооружения. В то же время наблюдается возрастающий интерес к использованию их в стационарных сооружениях в качестве покрытий спортивных залов или всего стадиона. С появлением нового материала для оболочек — стекловолокнистой ткани с покрытием из тефлона — во всем мире будет расширяться использование конструкций такого рода и одновременно станут совершенствоваться методы их проектирования.

Воздухоопорные конструкции подразделяются на два подвида — с оболочками, усиленными канатами, и без усиления. Мембрана воздухоопорных усиленных оболочек натянута между двумя канатами, которые служат первоначальной конструктивной системой. Прочность канатов на растяжение значительно выше, чем ткани, и, следовательно, они представляют собой элементы, воспринимающие основную нагрузку. Кроме того, канаты в значительной мере ограничивают деформации оболочки.

Для оболочек, усиленных канатами, конструктивный расчет должен включать в себя изучение прочности как оболочки, так и канатов. Обычно такую конструкцию можно рассматривать как тросовую сеть и совершенно не принимать во внимание прочность самой мембраны. Анализ сплошных мембран в принципе подобен анализу тросовых сеток, однако более сложен. В этой статье рассматриваются оболочки, не усиленные канатами.

Воздухоопорные конструкции относятся к категории неустойчивых, и при их анализе возникает необходимость рассмотрения двух различных этапов расчета:

• 1) определение первоначальной геометрии, когда равновесное состояние оболочки устанавливается под действием внутреннего давления и постоянной нагрузки;
• 2) анализ статической и динамической реакций оболочки, обладающей первоначальной геометрией, на прилагаемые внешние нагрузки.

Оба этапа приставляют собой геометрически нелинейные задачи. При определении первоначальной геометрии должны быть удовлетворены условия равновесия. При анализе реакции оболочки на приложение внешних сил большое значение имеет геометрическая жесткость, связанная с напряженным состоянием оболочки, поскольку рассматриваемые конструкции не имеют обычной упругой жесткости в первоначальной стадии деформирования.

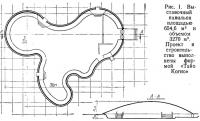
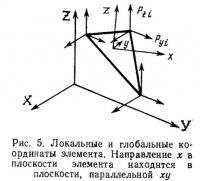
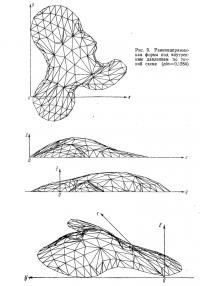
В данной статье изложен процесс проектирования пневматических конструкций, особенно конструкций на произвольном контуре. В качестве примера рассмотрена пневматическая конструкция покрытия выставочного павильона в Японии (рис. 1).


При проектировании решались следующие основные задачи.

1. Определение формы поверхности. Описан метод получения формы оболочки при равномерном ее натяжении внутренним давлением. Поскольку поверхность оболочки аналитически не задана, численный анализ применим только к задаче определения формы.

2. Раскрой в соответствии с требуемой формой. Приведен метод численного определения выкройки оболочки, необходимой для получения покрытия желаемой формы. По этому методу выкройки получают автоматически с помощью графопостроителя.

3. Статический расчет. Матрицы, необходимые для расчета пневматических конструкций, составлены на основе принципа виртуальных работ. Расчеты на воздействие снеговой нагрузки, ветра и внутреннего давления выполняют методом конечных элементов применительно к мембранам, испытывающим большие перемещения.

4. Динамический расчет. Этот расчет базируется на методе конечных элементов с использованием итерационной процедуры при постепенном загружении. Метод учитывает особенности мембранных конструкций, т. е. значительные деформации и изменение геометрии,/ линейные и ортотропные характеристики материала, изменения системы конструкции из-за неспособности ее элементов к сопротивлению сжатию. Для определения основных характеристик колебаний конструкции принята простая динамическая нагрузка.

Определение формы. Пневматические сооружения рассматривают как новый вид конструкций с той точки зрения, что первоначальная их геометрия при наличии внутреннего давления должна определяться до того, как начинается обычный анализ напряжений в результате действия внешних нагрузок.

Возможная конфигурация пневматического сооружения связана с условием, что его геометрия может обеспечить равновесие между внутренним давлением и напряжениями в оболочке.

Понятие «определение формы» означает выбор из ряда возможных именно той формы, которая обеспечит конфигурацию поверхности, удовлетворяющую архитектурным и строительным требованиям, а также установление зависимости формы поверхности от действующих усилий.


Проблема нахождения формы пневматических конструкций изучалась с разных точек зрения. Имеется ряд методов анализа, которые позволяют найти удовлетворительную форму поверхности в соответствии с внутренним давлением при заданном распределении напряжений в оболочке и известных граничных условиях.

Оболочки из растяжимых тканей при действии постоянного натяжения сохраняют длительное время свою форму и геометрическое подобие только при условии, если напряжения, которые испытывает оболочка, равновелики в каждой точке и в каждом направлении. Деформативность таких материалов оболочки, как ткани с покрытием, сравнительно велика. Поэтому для предварительного расчета пневматических сооружений важно представить форму оболочки при одинаковом во всех направлениях натяжении.

Форма пневматических оболочек, равнонапряженных внутренним давлением, определяется исключительно условиями контура и высотой ее подъема. Экспериментально мы получали такие формы с помощью мыльных пленок. Оболочка с равномерным напряжением идентична минимальной поверхности, облегающей заданный объем. Хотя получить мыльные пленки обычно очень просто, измерить их геометрию довольно сложно. Разработаны методы визуального наблюдения и освещения мыльных пленок для фотограмметрической их оценки, однако для обеспечения высокой точности измерения требуется большое мастерство экспериментатора.

Рассмотрим два метода получения формы равнонапряженной оболочки при внутреннем давлении.

По первому методу напряженное состояние оболочки описывается нелинейными дифференциальными уравнениями, разрешаемыми численно. Второй метод заключается в использовании метода конечных элементов для определения формы (предполагается, что поверхность состоит из конечных элементов плоской треугольной формы).

1. Решение с помощью метода конечных разностей. Равнонапряженная поверхность имеет среднюю кривизну Н.


где R₁, R₂ — радиусы главных кривизн; р — внутреннее давление; n₀ — напряжение оболочки.


Это условие принимается в качестве характеристики равнонапряженной поверхности. Когда поверхность задана как Z=Z(x, у) в декартовых координатах, дифференциальное уравнение формы равионапряженной поверхности в частных производных без учета собственного веса оболочки имеет вид


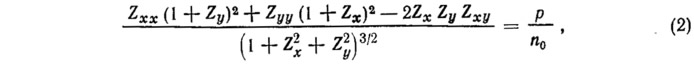
где индексы при Z обозначают дифференцирование по х, у.

Для случая полярных координат Z(r, Ф) частное дифференциальное уравнение приобретает вид


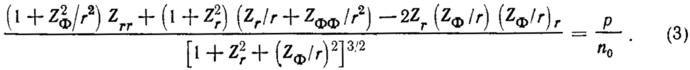
За исключением нескольких особых случаев, для которых возможны точные решения, уравнения (2) и (3) могут быть решены только численными методами. Известно несколько методов численного решения этих дифференциальных уравнений, и возможность их использования для пневматических сооружений обсуждалась рядом авторов. Однако численные методы применимы только к оболочкам, связанным с жестким контуром. В тех случаях, когда контуром служат канаты, мы получаем два взаимозависимых нелинейных дифференциальных уравнения. Эта задача почти неразрешима.

В таком случае рекомендуется рассчитывать сооружения данного типа с помощью метода конечных элементов.

Уравнение (2) может быть записано в конечных разностях. Тогда вместо решения дифференциального уравнения дается приближенное решение в виде системы алгебраических уравнений, как правило, нелинейных.


Заменим дифференциалы разностями


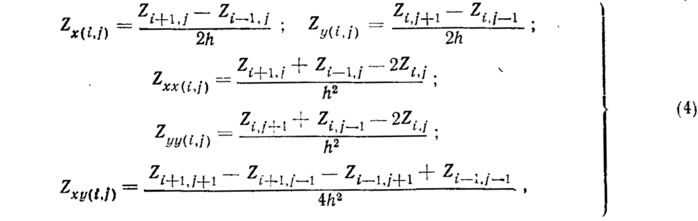
h — размер квадратной ячейки сетки, образованной координатами x=const и y=const в точке решетки (i, f).

Можно найти приближенное значение координат поверхности (Z_i,j).

Для каждой внутренней точки (i, f) получаем следующие разностные уравнения:


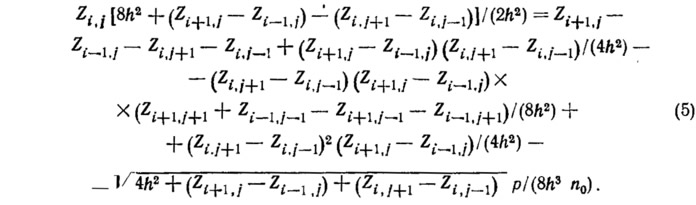
Граничные условия задаются обычно фиксированными координатами внешних точек контура.

Решение системы уравнений (4) относительно координат внутренних узлов сетки может быть осуществлено методом Гаусса — Зайделя. Этот метод заключается в том, что сначала устанавливают исходные величины координат Z_y в качестве первого приближения. Для оболочек, которые подвергаются действию нагрузок, характерных для пневматических сооружений, метод Гаусса — Зайделя дает обычно плохую сходимость, а если стрела подъема оболочки довольно высока, то сходимость вообще не может быть достигнута. Однако программа Гаусса — Зайделя для ЭВМ очень проста.


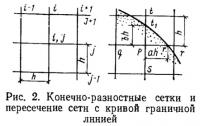
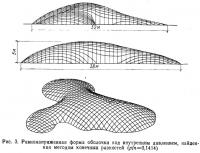
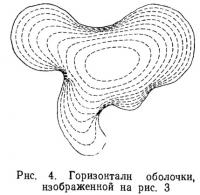
Когда контур криволинеен (рис. 2), он обычно не проходит через узловую точку, и граничные условия выражаются неэквидистантными конечными разностями. На рис. 3 и 4 показана форма, полученная конечно-разностным методом.

2. Решение с помощью метода конечных элементов. Разбиение поверхности оболочки на элементы ведет обычно к искривленным элементам. В большинстве случаев, однако, можно получить хорошее приближение геометрии оболочки путем сборки плоских элементов треугольной и четырехугольной формы. Для оболочки произвольного вида могут быть использованы треугольные элементы, как показано на рис. 5. С помощью треугольных элементов легко оперировать с неправильными формами и варьировать размер ячеек вблизи мест концентрации напряжений.

Важно подчеркнуть, что при использовании плоских элементов бывают ошибки, связанные с принятыми функциями перемещений. Однако эти геометрические ошибки уменьшаются по мере уменьшения размера ячеек.

Искривленные элементы позволяют более точно отражать геометрию оболочки. Об искривленных элементах оболочки опубликовано мало данных. При расчете пневматических сооружений чаще всего используют треугольные элементы. Для искривленной поверхности оболочки следует учитывать ошибки геометрической дискретизации, вызванные использованием плоских элементов.


Использование совершенно плоских элементов может быть выгодным для сооружений с гладкой поверхностью. Однако для сооружений с изогнутой поверхностью сложной геометрии ошибки дискретизации могут свести на нет преимущества плоского элемента. Пневматические сооружения, как правило, имеют гладкую поверхность.

В этой статье описывается метод определения формы оболочки, испытывающей равномерное напряжение под действием внутреннего давления, с использованием треугольных плоских элементов.

Рис. 5 изображает треугольный элемент оболочки, не обладающий изгибной жесткостью. Уравнения равновесия в узле i составлены исходя из условий постоянства полной потенциальной энергии:


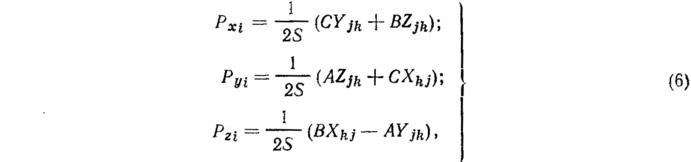
где уравнение плоскости записывается в виде


а уравнение плоскости, проходящей через заданные точки i, j, k, может быть записано в виде детерминанта


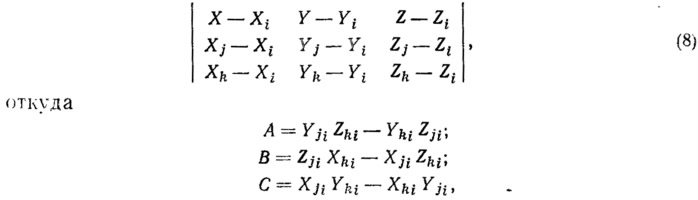
где X_ji=Х_j—X_i и т. д.

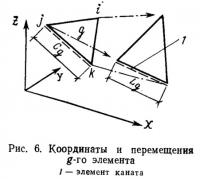
Когда добавляются усиливающие или обтягивающие канаты, принимающие на себя часть нагрузки, функция потенциальной энергии П может быть записана в следующем виде по отношению к определяемому элементу g, показанному на рис. 6:


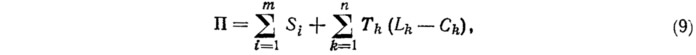
где S_i — площадь треугольного элемента i; — длина элемента каната после деформации; C_h — первоначальная длина элемента каната; T_k — множитель Лагранжа.

Следует заметить, что условие постоянной длины каната должно быть введено как вспомогательное.

В уравнении (9) независимые переменные — это координаты узлов и множитель Лагранжа Т_k. Из условия полной потенциальной энергии по отношению к X, Y, Z мы имеем следующие уравнения:


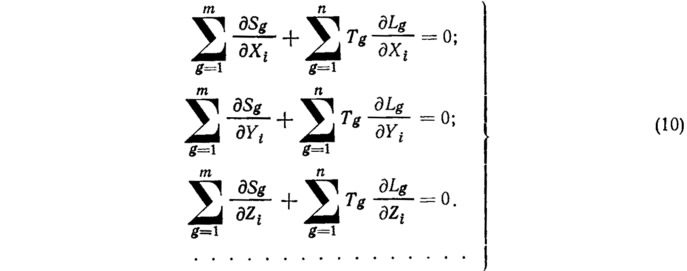
Очевидно, что уравнения (10) являются уравнениями равновесия узлов, записанными с учетом геометрии после деформации. На основании другого условия постоянства энергии по отношению к Т_k мы имеем дополнительное условие равновесия элемента подкрепляющего каната, т. е.


Уравнения (10) и (11) образуют основные совместные уравнения с неизвестными координатами узлов и множителями Лагранжа. Для решения этих нелинейных совместных уравнений может быть применен метод Ньютона—Рафсона.

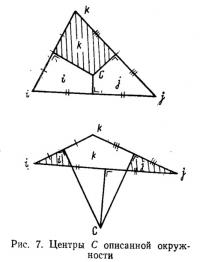
Нагрузки от внутреннего давления на элемент пропорциональны трем площадям, на которые делится окружность, описанная вокруг треугольного элемента (рис. 7).

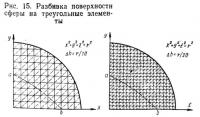
Точность. Трудно говорить об ошибках в общих случаях, однако в каждом отдельном случае ошибка может быть установлена путем сравнения с известными точными решениями, где использованы два или более вида элементов. Примером такого рода является решение для сферы.


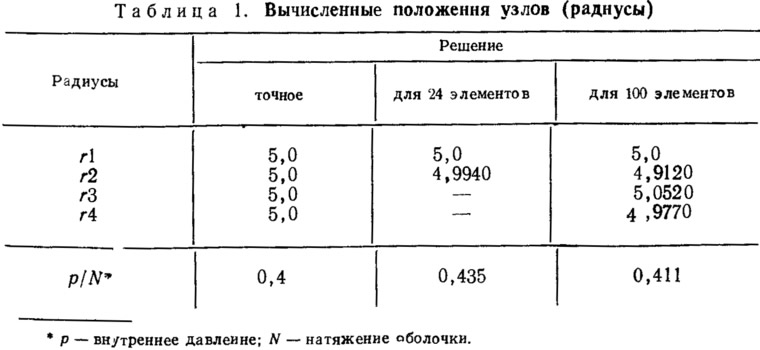
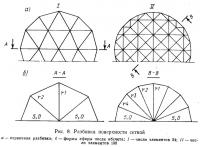
Используются два вида деления на элементы, и результаты, приведенные в табл. 1, показывают, что при использовании элементов меньшего размера существенныхуточнений не достигается. Это указывает на то, что сходимость физической аппроксимации с подлинной формой при плоских треугольных элементах бывает хорошей и достаточно точной для практического применения (рис. 8).

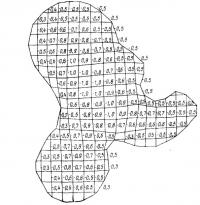
Результаты. Сходимость в данном примере происходила медленно, и после 135 циклов по методу Гаусса — Зайделя максимальное отклонение уравновешивающей силы составило лишь 0,122% нормальной узловой нагрузки.

В процессе вычисления некоторые элементы находят на другие. Во избежание этого устанавливается предел смещений. Такая неустойчивость является следствием идеализации поверхности при представлении ее плоскими треугольниками. Этот недостаток можно устранить, используя более сложно изогнутые элементы или усовершенствуя сетки ячеек там, где элементы разрушаются. Результаты, полученные после 135 циклов по методу Гаусса—Зайделя, показаны на рис. 9.

Приближенное решение. Условия равновесия внутренних и внешних сил могут быть записаны в виде


Конечные, элементы, не обладающие упругой жесткостью, но остающиеся в равнонапряженном состоянии, соответствуют мыльной пленке, потенциальная энергия которой оценивается в зависимости от напряжения ее поверхности. Эти элементы обладают только герметрической жесткостью.

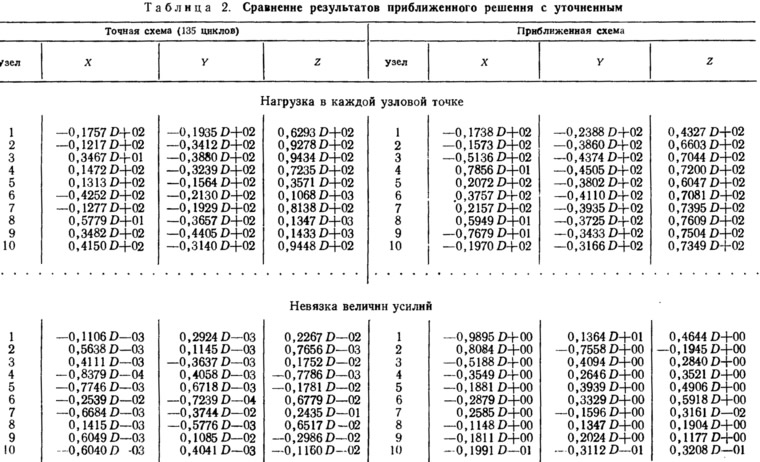
Используя их, можно получать надувные формы равного напряжения. Такой приближенный метод дает хорошую сходимость за несколько первых циклов. Результаты и их точность показаны на рис. 10 и в табл. 2.

Цель расчета заключается в том, чтобы получить потенциально эффективную форму для последующего использования в качеству конструкции, а не в том, чтобы выполнить детальный анализ. Поэтому сходимость можно считать удовлетворительной.

Раскрой с целью получения желаемой поверхности

Материал, из которого делают оболочки, не сжимается и не растягивается, как резина. Следовательно, этот материал нужно раскроить и сшить так, чтобы получить желаемую форму криволинейной поверхности. Подобная операция очень проста, если требуется получить сферическую или цилиндрическую поверхность. Однако, если оболочка имеет сложную форму, то раскрой требуемой поверхности представляет собой трудную задачу. Ниже описан способ раскроя, обеспечивающий получение желаемой формы.

Геодезические линии. Когда поверхность нельзя выразить уравнением, предполагается, что геометрические характеристики гладкой криволинейной поверхности могут быть удовлетворительно представлены геометрическими характеристиками многогранной поверхности, построенной из небольших плоских элементов.

Геодезические линии на криволинейной поверхности аппроксимируются геодезическими линиями на многограннике. По мере уменьшения размеров элементов должно произойти полное совмещение. Опыт показывает, что такое совмещение действительно имеет место.

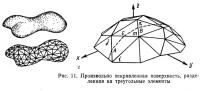
Произвольно искривленная поверхность, разделенная на треугольные элементы, показана на рис. 11. Рассмотрим типичные элементы, обозначенные буквами i, j, m и j, m, n. Глобальные координаты трех узловых точек определяют плоскость элемента. Пусть А и В обозначают две заданные точки на каждом треугольном элементе и пусть точка С лежит между двумя элементами.

Длина (AC+СВ) становится самой короткой, когда угол jCA равняется углу mСВ, т. е. когда линия АСВ является геодезической линией. Это можно проделать далее со следующим элементом и продолжить процесс до границы оболочки.

Геодезическая линия, проходящая через любую обычную точку на поверхности, однозначно определяется ее направлением через точку или двумя заданными точками на поверхности. Направление геодезической линии должно быть найдено после общего рассмотрения.

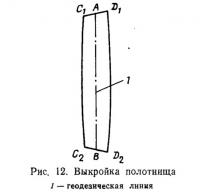
Если полосу бесконечно малой ширины с геодезической линией в качестве центральной линии вырезать из поверхности и развернуть в плоскость (рис. 12), то центральная линия A—В может стать прямой, в то время как С₁, С₂ и D₁, D₂, очевидно, не будут лежать в ее плоскости, поскольку узкая полоса неразвертываема. Это означает, что геодезическая линия на поверхности может быть определена как кривая, соприкасающаяся плоскость к которой в каждой точке содержит нормаль к поверхности в этой точке. Поверхность, образованная из плоских полос, будет только приближением к континуальной поверхности. Предварительное натяжение в границах допустимого напряжения улучшит форму оболочки.

Многочисленные определения выкроек методом геодезических линий с помощью ЭВМ показали его приемлемость как в отношении точности, так и с точки зрения его трудоемкости.

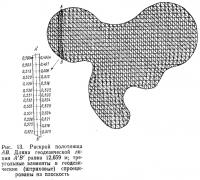
Изготовление выкройки. После вычисления геодезических линий на поверхности можно установить форму выкроек, вычислив с помощью ЭВМ расстояние между двумя соседними линиями. Выкройки получаются автоматически с помощью графопостроителя (рис. 13 и 14).

Рис. 13. Раскрой полотнища АВ >

Рис. 14. Раскрой полотнищ оболочки >

Рис. 15. Разбивка поверхности сферы на треугольные элементы >

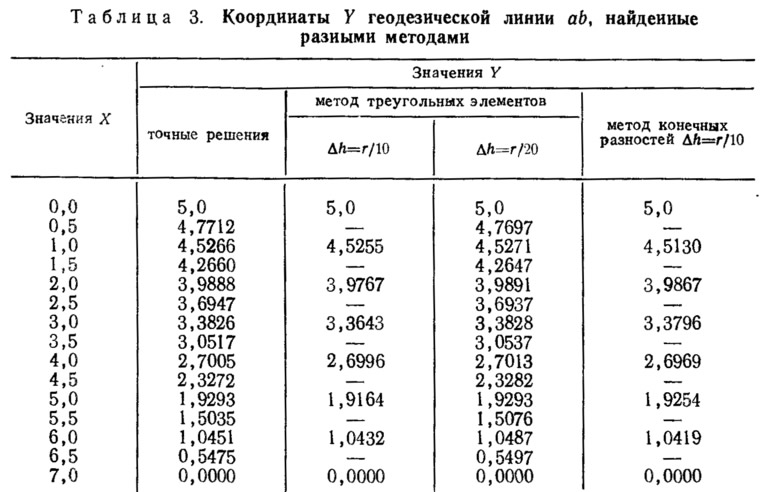
Точность метода. В табл. 3 приведены координаты геодезической линии ab на сфере, вычисленные представленным здесь методом (см. рис. 12), в сравнении с данными, полученными точным решением. Как видно из этой таблицы, метод дает хорошие результаты, несмотря на то, что криволинейная поверхность аппроксимирована плоскими треугольными элементами (рис. 15).

Анализ статической и динамической реакций оболочки

Следующим шагом при расчете конструкции является анализ статической и динамической реакции сооружения заданной первоначальной геометрии на прилагаемые внешние силы.

Деформации пневматических сооружений в результате действия нагрузок довольно велики, поэтому расчет оболочек содержит нелинейные задачи, учитывающие геометрические и физические нелинейные зависимости. Однако в большинстве случаев нелинейное поведение материалов во внимание не принимается, так как диапазон напряжений самой оболочки практически не слишком велик.

Хотя первоначальные попытки анализа оболочки носили характер решения дифференциальных уравнений, записанных для непрерывно изогнутой поверхности, применение матричных методов было признано более целесообразным и практичным для оболочек произвольной формы.

В последнее время многие авторы анализировали геометрически нелинейные задачи пневматических сооружений, используя метод матриц перемещений. Результатов аналитических исследований опубликовано пока очень мало. В связи с трудностями, возникающими при решении математических задач, пожалуй, наиболее популярны сейчас численные методы. Однако некоторые попытки выполнить аналитические исследования все же предпринимались. Р. Тростель и Ф. Шлейер [10] дали исчерпывающие математические формулировки для решения некоторых задач по мембранам и мембраноподобным оболочкам. Дж. Леонард [13] разработал метод возмущения для расчета без использования ЭВМ оболочек вращения на действие избыточного давления и эксплуатационных нагрузок.

Хотя ясно, что применение такого рода аналитических решений ограничено, изучение физического характера работы оболочек простой формы оказалось желательным для получения более; полного представления об их поведении.

Метод конечных элементов. Для анализа сооружений используют идеализированный конечный элемент и возможности системы счисления с помощью матриц. Методу конечных элементов на практике отдают предпочтение из-за преимуществ, очевидных при анализе сооружений неправильной конфигурации. Этот хорошо разработанный метод анализа в сочетании с широкими возможностями, предоставляемыми вычислительными машинами, позволяет рассчитывать сложные строительные конструкции. Следствием опыта, приобретенного при использовании данного метода, явилосб убеждение, что для большинства современных строительных конструкций линеаризированный расчет оказывается неадекватным.

В рассматриваемом здесь методе расчета сделана попытка сохранить гибкость применения характеристик идеализированного конечного элемента мембраны, уточнив, однако, картину поведения конструкции, для чего требуется исключить некоторые традиционные линеаризующие допущения.

Методы анализа сооружений, основанные на идеализации элемента, разделяются на методы перемещений, сил и комбинированные. Геометрические нелинейности удобнее всего изучать с помощью метода перемещений, тогда как нелинейность упругих материалов легче учитывается методом сил. Задачи, в которых следует принимать во внимание как геометрические, так и физические нелинейности, лучше всего решать, применяя комбинированный метод.

Для мембранных конструкций, таких как пневматические, ситуации, включающие геометрические нелинейности, но ограниченные линейным поведением упругого материала, образуют важный класс проблем для анализа.

Хорошо известно, что каждый из трех общих прямых методов соответствует определенной формулировке энергии. Метод перемещений эквивалентен принципу постоянства потенциальной энергии, который гласит, что все удовлетворяющие геометрической приемлемости перемещения, которые делают потенциальную энергию постоянной, удовлетворяют условиям равновесия и являются действительными перемещениями.

Основные уравнения. Основное условие равновесия внутренних и внешних сил следующее [12]:


где {ψ} — вектор суммы внешних и внутренних сил; [В] — матрица упругих констант изотропного или ортотропного материала; {σ} — вектор напряжений; {R} — вектор внешних сил; {δ} — вектор перемещений.

[В] определяется из соотношения для деформаций как


где [В₀] — линейная, а B_L — нелинейная части [В], зависящие от перемещений. Отнесенные к прямоугольной системе координат перемещения u, v и w определяют деформации как:


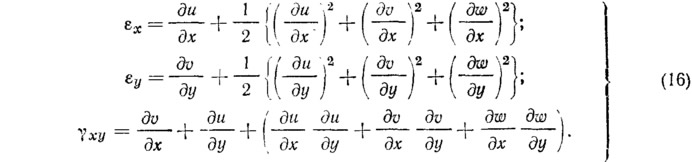
Поскольку необходимо использовать процесс Ньютона—Рафсона, следует найти соотношения между d{δ} и dφ. Таким образом, взяв соответствующие варианты уравнения (13) по отношению к d{δ}, получим:


Поскольку все решения могут быть выполнены с применением одноступенчатой операции, при решении задачи полной нагрузки возникает, как и во всех нелинейных задачах, возможность неодинарного решения и может быть получено физически невозможное решение. В таких случаях рекомендуется продолжать увеличение нагрузки, получая нелинейные решения для каждого шага увеличения.

В уравнении (20) матрицы [В] и [К] даны для треугольной плоской мембраны, при этом функции перемещения для u, v и w приняты в виде линейных функций в элементе:


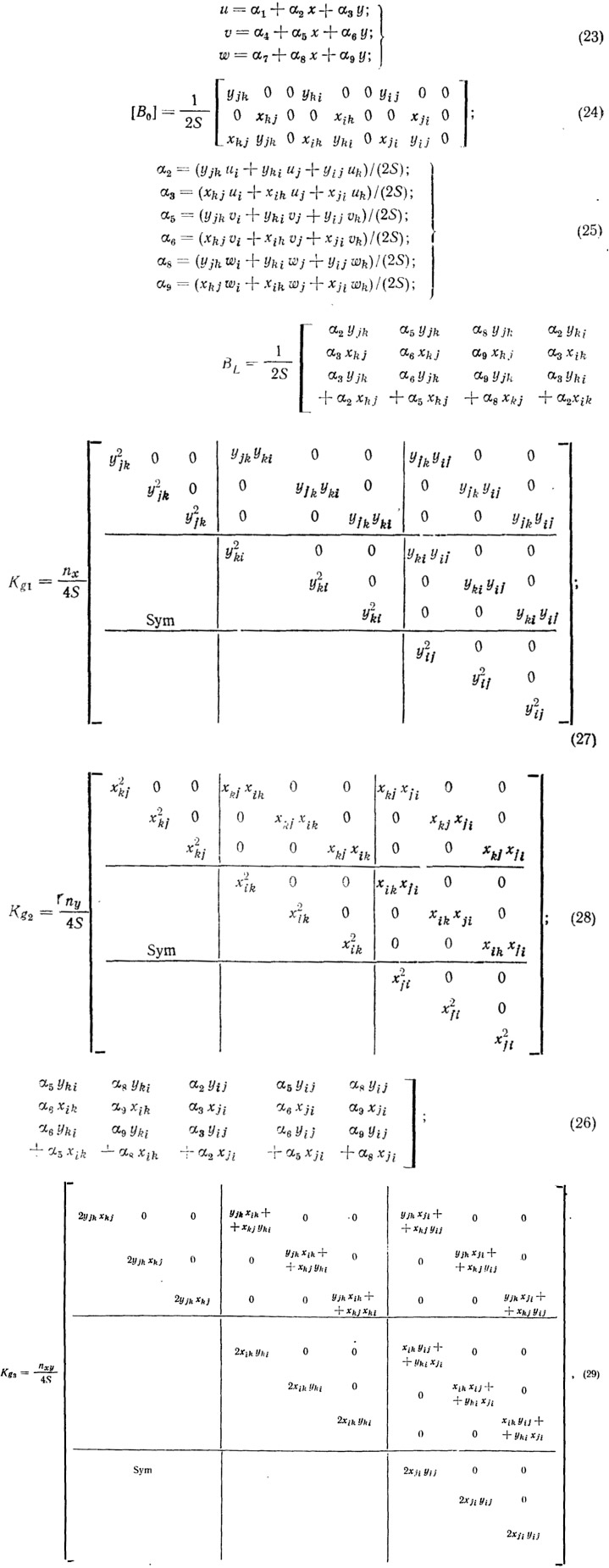
где n — мембранные усилия, зависящие от степени напряжения; S — площадь элемента.

Геометрическая матрица жесткости


Поскольку ткань с покрытием обычно обладает ортотропными характеристиками, это следует учесть при расчете.

В таком случае матрица [D] выглядит следующим образом [11]:


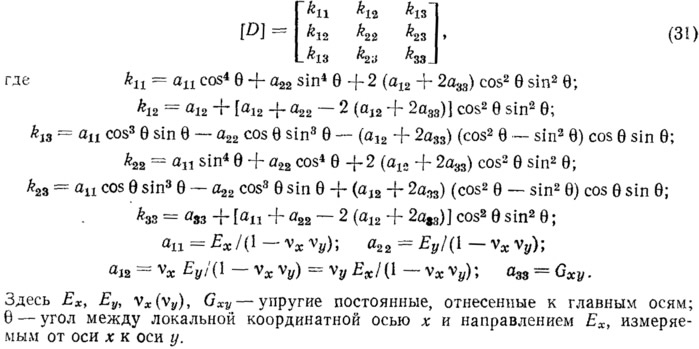
Метод решения. Использование метода конечных элементов приводит в итоге к системам совместных нелинейных алгебраических уравнений. Для решения этих нелинейных уравнений эффективно используется метод Ньютона—Рафсона.

Образование морщин. Если напряжения в конечном элементе не удовлетворяют условию


то усилия N_x или N_y и N_xy приравниваются нулю для следующего итерационного цикла Ньютона. Если оба главных усилия станут отрицательными, то они равны нулю. В таком случае сходимость итерационного процесса Ньютона—Рафсона происходит медленно.

Узловые нагрузки от распределенного давления, приложенного к поверхности элемента, рассматриваются для деформированной оболочки. На каждом шаге увеличения нагрузки вычисляется разность между прилагаемыми нагрузками и нагрузками, приложенными к деформированной оболочке. Разность вычисляется каждый раз до тех пор, пока невязка не будет в заданных пределах.

Узловые нагрузки от распределенного по поверхности элемента давления делятся на три части в соответствии с площадями элемента, определяемыми с помощью построения описанной окружности (см. рис. 7).

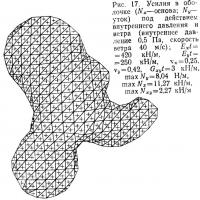
Числовой пример. Выставочное сооружение, изображенное на рис. 1, было рассчитано численным методом на действие внутреннего давления, а также ветровой и снеговой нагрузок. Материал характеризовался следующими механическими свойствами: E_xt=420 кН/м; E_yt=250 кН/м; v_x=0,25; v_y=0,42; G_xyt=3 кН/м.

Эти значения были получены при одноосном испытании на растяжение, которому подвергалась ткань с покрытием. Зависимость «напряжение—удлинение» для тканей с покрытием нелинейная. Более того, после разгрузки образца наблюдается отклонение кривой «напряжение — удлинение» от первоначальной формы вследствие того, что такие материалы являются одновременно нелинейными и неупругими.

Тем не менее, в некоторых случаях кривые «напряжение—удлинение», полученные в результате испытания тканей с покрытием на разрыв, в ограниченном диапазоне нагрузки проявляют свойства, близкие к линейно-упругим. На это следует обратить внимание, и такой материал при практических расчетах можно рассматривать как линейно-упругий.

Результаты измерений коэффициентов Пуассона v_x и v_y показали их зависимость от напряжения, а также то, что измеренные коэффициенты Пуассона не удовлетворяли теории «обратных величин». Однако в целях упрощения расчета здесь приняты обычные коэффициенты Пуассона.

Жесткость при сдвиге G_xyt мала по сравнению с Et. Оценка напряжений не будет связана с трудностями, если величину G_xyt принять небольшой, что характерно для всех тканей с покрытием.

Физические константы материала установлены, как написано выше, на основе результатов измерения. Направление вдоль основы принимается за ось х, а направление по утку — за ось у. Полученные результаты показаны на рис. 16—19.

Рис. 17. Усилия в оболочке под действием внутреннего давления и ветра >

Рис. 18. Вертикальные перемещения под действием ветра и внутреннего давления >

Рнс. 19. Вертикальные перемещения под действием снеговой нагрузки >

Расчет на динамические нагрузки

Немаловажным моментом при проектировании пневматических сооружений является расчет на динамические нагрузки. Хотя некоторые авторы рассматривали эффекты завихрения и аэродинамической неустойчивости, основной строительной динамической проблемой, по-видимому, остается учет порывов ветра.

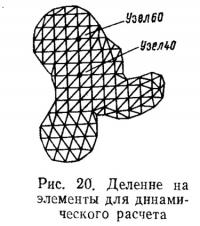
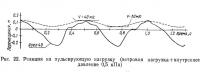
Для определения основных характеристик сооружения рассмотрим простую динамическую нагрузку с помощью модели из конечных элементов, изображенной на рис. 20.

Для нелинейных динамических задач, включающих значительные перемещения и зависящие от них внешние силы, уравнение движения может быть записано следующим образом:


Метод решения. Расчеты общей динамической реакции нелинейных систем, в которых используются шаговые процедуры численного интегрирования, могут быть осуществлены путем разделения общего времени на последовательные конечные приращения (инкременты) времени и вычисления реакции по окончании каждого инкремента Δt в виде первоначальных условий и нагрузки в течение инкремента. В этой статье для решения уравнения (33) применен β-метод Ньюмарка.

β-метод Ньюмарка. В этом методе скорость и перемещение в конце инкремента времени Δt выражаются через ускорения, скорости и перемещения в начале инкремента времени, а также через ускорения в конце инкремента времени.

Эти уравнения принимают вид:


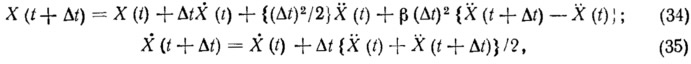
а ускорение в конце инкремента времени дается в виде:


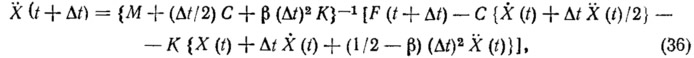
где β — параметр интегрирования.

При β=1/б имеем хорошо известный метод линейного- ускорения.

Численные результаты. Сооружение, показанное на рис. 1, было представлено конечными элементами, как показано на рис. 20.

Жесткость элемента, являющаяся нелинейной, определяется уравнениями (24)—(31), и предполагается наличие присоединенных масс. Для получения основных характеристик сооружения нужно рассмотреть задачу свободных колебаний (рис. 21).

Материал ортотропен и имеет следующие показатели: Е_х=420 МПа, Е_у=250 МПа, G_xy=3 МПа, толщина материала t=0,1 см.

Скорость ветра V может быть разделена на компонент средней скорости v и компонент флуктуации v:


Средняя скорость ветра вызывает давление


которое может быть добавлено к постоянным нагрузкам на оболочку, образуя вектор нагрузки {R}. Равновесное состояние может быть установлено путем статического расчета. Представление о флуктуационной скорости ветра получить гораздо труднее; имеется мало информации относительно пространственного распределения давления ветра как временной функции. Представление о ветре, таким образом, дают скорости, показанные на рис. 22.

Большая часть энергии в турбулентном потоке сконцентрирована в диапазоне частот от 0,1 до 1 Гц. Следовательно, если сооружение таково, что ни одна из частот не входит в данный диапазон, динамический эффект ветровой нагрузки не будет превалирующей частью ее воздействия. Пневматические сооружения приобретают жесткость в результате внутреннего давления, их вес в нормальных условиях очень мал. Поскольку частота меняется обратно пропорционально массе, частота колебаний таких систем очень высока, и они не попадают в категорию сооружений, которые могут оказаться под динамическим воздействием ветровой нагрузки, за исключением случаев чрезвычайно низкого внутреннего давления.

Для получения более точных результатов должны быть учтены следующие моменты:

• оценка сил ветра;
• разница в результатах между LM и СМ для матрицы масс;
• влияние размера ячейки элемента;
• оценка коэффициента затухания;
• влияние присоединенной массы;
• взаимодействие между внутренним давлением и ветром.

Заключение

Законченная конструкция, для которой использована полиэфирная ткань, покрытая ПВХ, показана на рис. 23. Она имеет следующие характеристики: переплетение — простое; масса — 993 г/м²; толщина — 0,93 мм; прочность полоски на разрыв: по основе — 3,40 кН/3 см, по утку — 2,83 кН/3 см.

Список литературы

• 1. Barnes, М. R., «Form-Finding of Minimum Surface Membranes», Proc. of I. A. S. S. World Congress on Space Enclosures, Montreal, 1976.
• 2. Haug, E., «Finite Element Analysis of Non-linear Membrane Structures», Proc. of I. A. S. S. Pacific Symposium on Tension Structures and Space Frames. Tokyo, 1971.
• 3. Ishii, K-, «Shape of Membrane Structures», Proc. of I. A. S. S. Pacific Symposium on Tension Structures and Space Frames. Tokyo, 1971.
• 4. Ishii, K., «On Developing of curved surface of Pneumatic Structures», Proc. of I. A. S. S. International Symposium on Air—Supported Structures, Delft, 1972.
• 5. Ishii, K., «Analytical Shape Determination for Membrane Structures», Proc. of I. A. S. S. World Congress on Space Enclosures, Montreal, 1976.
• 6. Ishii, K., «An Approach to Structural Design of a Pneumatic Structures», Proc. of I. A. S. S. International Symposium on Air-Supported Structures, Venezia, 1977.
• 7. Ishii, K., «Form Finding Methods of Pneumatic Structures», Research Report of IASS Working Group of Pneumatic Structures, 1978, West Virginia.
• 8. Knudson, W. C., «Response of Cable net Structures under Dynamic Loadings», Proc. of 1. A. S. S. Pacific Symposium on Tension Structures and Space Frames., Tokyo, 1971.
• 9. Newmark, N., «А Method of Computation for Structural Dynamics», ASCE EM3, July, 1959.
• 10. Otto, F., Trostel, R., «Tensile Structures I.» The MIT Press, 1967.
• 11. Uemura, М., «Deformation and Stress of Orthotropic Rectangular Membrane under Uniform Lateral Pressure», Proc. of I. A. S. S. Pacific Symposium on Tension Structures and Space Frames., Tokyo, 1971.
• 12. Zienkiwicz, О. C., «The Finite Element Method in Engineering Science». McGRAW—HILL Publishing Co. 1971.
• 13. Leonard, J. W., «Inflatable Shells: Pressurization Phase», Journal of the engineering mechanics div., ASCE Vol. 93, EM2, April, 1967.
• 14. Task Committee on Air-Supported Structures ASCE «State—of Art Report on Air Supported Structures», Published by ASCE, 1979.