Расчет воздухоопорных сооружений на ветровые нагрузки

1. Введение

Данная работа посвящена исследованию воздухоопорных оболочек при внутреннем давлении и ветровой нагрузке. После краткого изложения геометрически нелинейной теории мягких оболочек и гибких нитей рассмотрены в общем виде нагрузки, свойства материалов и методы практического расчета воздухоопорных оболочек. Более подробно рассмотрены полуцилиндрические оболочки с торцами на круговом и прямоугольном плане. Приведены некоторые результаты численного расчета усилий и перемещений; обсуждается напряженно-деформированное состояние оболочек и влияние на него различных факторов. Выведены приближенные линейные зависимости для определения основных усилий в форме, часто встречающейся в национальных нормах или инструкциях.

В статье рассматриваются главным образом полуцилиндрические воздухоопорные оболочки при действии ветровых нагрузок. В периоды необычайно сильных штормовых ветров, наблюдавшихся, например, в ФРГ в ноябре 1972 г., были случаи разрушения или повреждения воздухоопорных оболочек. Это показало, что при проектировании и расчете таких оболочек имеется еще ряд нерешенных проблем, а именно:

• установление нагрузок (требуемое внутреннее давление, интенсивность и характер распределения ветровой нагрузки);
• оценка напряженно-деформированного состояния конструкций (теория расчета, учет деформационных свойств материала, определение усилий и перемещений);
• надежность конструкций (прочность и длительные характеристики материала, значения и виды коэффициентов безопасности, причины отказов);
• правила эксплуатации (соблюдение безопасных расстояний от оболочки до находящихся под ней предметов, поддержание установленного уровня внутреннего давления).

Несмотря на обилие имеющихся данных испытаний на моделях и численных расчетов оценка напряженно-деформированного состояния воздухоопорных оболочек продолжает еще содержать ряд неопределенностей и неточностей. Это становится особенно очевидным из перечисления только наиболее важных факторов, влияющих на надежность результатов расчета. К ним относятся:

• геометрия конструкции (форма оболочки, ее габариты, очертание торцов);
• характер нагрузок (направление ветра, распределение ветрового давления по поверхности оболочки, внутреннее давление, интенсивность нагрузок);
• свойства материала (упругость и вязкость, анизотропия, физическая нелинейность, характеристики при кратковременной и длительной нагрузке, при одноосном и двухосном напряженных состояниях);
• вид соединений (влияние усилений оболочки в местах расположения швов);
• раскрой оболочек (отклонения от проектной формы).

Может оказаться существенным влияние и ряда других факторов. Определенные трудности вызываются еще и тем, что при численном расчете могут быть получены некоторые не вполне надежные данные, обусловленные как принятыми теоретическими предпосылками, так и самой процедурой расчета; эти данные нуждаются в надлежащей интерпретации, а в отдельных случаях могут привести к ошибкам в окончательных результатах.

Чтобы получить достаточно достоверные расчетные зависимости, мы ограничимся рассмотрением оболочек простейшего геометрического очертания — цилиндрических с закругленными торцами или на прямоугольном плане (см. далее рис. 1, а и б), без учета подкреплений тросами или усилений в местах расположения швов. При этом предполагается, что оболочки имеют идеальную геометрическую форму.

2. Теория мягких оболочек

2.1. Предварительные замечания. Воздухоопорные конструкции относятся к мягких большепролетным оболочкам. [3, 22]. Они выполняются из тканей с покрытиями и в ряде случаев подкрепляются тросами. Размер поперечного сечения оболочки (ее толщина) настолько мал по сравнению с пролетом, что изгибной жесткостью оболочки можно пренебречь. Таким образом, воздухоопорные оболочки принадлежат к классу мягких оболочек (мембран), в которых внешние нагрузки уравновешиваются только нормальными усилиями, а изгибающие моменты пренебрежимо малы. Поскольку при этом перемещения оболочек велики по сравнению с их общими размерами, для их расчета необходимо использовать геометрически нелинейную теорию. Относительные деформации оболочек, наоборот, в общем невелики, так что расчет можно производить в рамках физически линейной теории, тем более что количественное описание нелинейного поведения материала связано с большими трудностями. Поэтому в дальнейшем приводятся основные зависимости геометрически нелинейной и физически линейной теории мягких оболочек и гибких нитей (тросов), причем более детально рассмотрены возможные упрощения соотношений между относительными деформациями и перемещениями, а также особые случаи геометрии конструкций. Нелинейные теории оболочек разработаны в трудах многих авторов; теория мягких оболочек подробно изложена и рассмотрена на примерах в работе [22]. Ниже используется тензорная форма записи, принятая в общей теории оболочек [7].


2.2. Общая геометрическая нелинейная теория мягких оболочек. Полная система уравнений геометрически нелинейной теории однородных гиперупругих мягких оболочек построена в работе [7]. Будем полагать все величины отнесенными к начальному (ненапряженному и недеформированному) состоянию оболочки. Тогда значения трех усилий (n^αβ=n^βα), трех относительных деформаций (α_αβ=α_βα) и трех перемещений (u_α, u_β) определяются из следующих уравнений:


Индексы, обозначенные греческими буквами, принимают значения 1 и 2, причем суммирование по одинаковым верхним и нижним индексам производится в соответствии с соглашением Эйнштейна.

Приведенная выше система уравнений является «полной» в смысле оптимальной теории оболочек. Тензор относительных деформаций α_αβ образуется как разность метрических тензоров деформированной и недеформированной поверхностей оболочки α_αβ и α_αβ


и не содержит никаких упрощений. Уравнения равновесия (2.2) и (2.3), выведенные на основе вариационного принципа, являются, таким образом, также «полными» и не содержат каких-либо упрощений [7].

Удельная энергия формоизменения V является функцией аир и зависит от свойств материала. Например, для линейно-упругого материала



В данном случае тензор упругих характеристик E^αβρλ содержит, в силу свойств симметрии n^αβ и α_αβ только шесть констант материала. Для изотропного материала


причем свойства материала описываются всего двумя константами— модулем упругости Е и коэффициентом поперечной деформации v.


Для решения приведенных выше систем уравнений необходимо еще ввести граничные условия, которые целесообразно строить на основе вариационных принципов [7]. Ввиду высокой степени геометрической нелинейности уравнений (2.1) — (2.7) или (2.12) — (2.20) найти их решения (в аналитической или численной форме) чрезвычайно трудно или вообще возможно лишь для простейших случаев; поэтому представляется целесообразным их упрощение.

2.3. Упрощенные теории мягких оболочек. Если в уравнениях (2.1) — (2.3) последовательно опустить все величины, характеризующие геометрическую нелинейность, получим известную систему уравнений геометрически линейной теории мягких оболочек:



Дополняя тензор относительных деформаций (2.22) простейшим нелинейным слагаемым u_3,αu_3,β/2, получим систему уравнений упрощенной геометрически нелинейной теории мягких оболочек 1-го порядка (типа Доннела—Маргерра):


Естественно, что упрощенное представление относительных деформаций (2.27) последовательно приводит также к упрощению условий равновесия и, равным образом, граничных условий. В работе [7] вывод упрощенной (но совместной) системы уравнений (2.25)—(2.28) осуществлен на основе вариационного принципа. Путем дополнения (2.27) или упрощения (2.1) можно, конечно, построить и другие системы уравнений; при этом неизбежно придется изменить формулировку условий равновесия, но таким образом, чтобы они не противоречили основным принципам механики.

Для оболочек в форме кругового цилиндра в соответствии с нелинейной теорией 1-ro порядка имеем:


Уравнения состояния сохраняются в прежнем виде.


2.4. Общая геометрически нелинейная теория гибких нитей (тросов). На основе полной системы уравнений общей геометрически нелинейной теории мягких оболочек (2.1)—(2.7) могут быть записаны эквивалентные уравнения теории гибких нитей. Если, например, геометрия нити описывается одной координатой θ², то опуская все величины, зависящие от координаты θ¹, получим систему уравнений геометрически нелинейной теории однородных гиперупругих нитей, в которой все величины, как и выше, отнесены к начальному (ненапряженному и недеформированному) состоянию. При этом значения усилий n²², относительных удлинений α₂₂ и перемещений u₂, u₃ определяются из следующих четырех уравнений:


Необходимо иметь в виду, что здесь ковариантная производная образуется в том же смысле, что и в теории мягких оболочек, дифференцированием по одной координате θ².

Как и в теории мягких оболочек, приведенная система уравнений является «полной» в смысле оптимальной теории линейных (двухмерных) систем. Она должна быть еще дополнена граничными условиями, которые могут быть выведены на основе вариационного принципа.

Ниже рассмотрим подробнее гибкие нити кругового очертания в связи с их особым значением для расчета цилиндрических воздухоопорных оболочек и простотой их геометрического описания.

2.5. Геометрически нелинейные теории круговой гибкой нити. Обозначив через R радиус окружности нити и через θ² текущее значение центрального угла, а также учитывая, что в данном случае a²²=R²; a²²=1/R; b₂₂=R; b₂₂=1/R; b²²=1/R³, получаем полную систему уравнений геометрически нелинейной теории круговой гибкой нити:


Отметим, что здесь ковариантная производная превращается в частную производную. Если заменить в уравнениях (2.39)—(2.42) тензорные величины обычными «физическими» величинами, получим окончательно систему уравнений в виде:


Для простоты материал нити в уравнении (2.46) принят) линейно-упругим.

На основе уравнений (2.43)—(2.46) может быть построен ряд упрощенных теорий. Для начала, опуская последовательно все величины, характеризующие геометрическую нелинейность, получим систему уравнений:


Из уравнений равновесия непосредственно следует:


что не имеет смысла, поскольку нагрузка должна иметь ограниченную величину. Таким образом, «геометрически линейная» теория гибкой нити не имеет практического значения; приведенные уравнения соответствуют лишь особому случаю нерастяжимой нити, нагруженной равномерным внутренним давлением р=—р_i=const. В этом случае, когда D→∞, уравнение (2.50) теряет смысл, и остается одно уравнение (2.49), приводящее к известному выражению


Из этих двух простых примеров уже видно, что на основе общей системы уравнений (2.43)—(2.46) может быть, вообще говоря, построено множество упрощенных теорий. Однако при этом следует всегда иметь в виду, что соотношения между удлинениями и перемещениями и условия равновесия не должны противоречить друг-другу и что надлежащим образом должны быть заданы также граничные условия. Такого рода теории, чтобы обеспечить их «совместность», целесообразно строить на основе вариационных принципов. Следует также особо проверять (как это было показано выше), удовлетворяет ли формально построенная теория основным принципам механики.

2.6. Дополнения. Воздухоопорные оболочки имеют еще некоторые особенности, на которых мы коротко остановимся. Вследствие своей весьма малой изгибной жесткости оболочка не может воспринимать сжимающих усилий. Поэтому уровень предварительного напряжения оболочки внутренним давлением должен быть достаточно высоким, чтобы создаваемые им растягивающие усилия не «погашались» полностью внешними нагрузками (например, от снега), за исключением, может быть, отдельных небольших участков оболочки. Появление в оболочке «сжимающих напряжений» приводит, в частности, к образованию складок.

Жесткость при растяжении D материала оболочек в большинстве случаев настолько велика, что его относительные удлинения пренебрежимо малы. В связи с этим может оказаться целесообразным использование в расчетах приближенных решений теории чистого изгибания оболочек [6], в которой относительные деформации принимаются тождественно равными нулю. При этом уравнения состояния отпадают. Условием возможности применения данной теории является физическая осуществимость соответствующего деформированного состояния оболочки. В рассматриваемом случае общая система уравнений (2.1)—(2.4) упрощается и принимает вид:


где обозначения даны в уравнениях (2.5)—(2.7). Из этих уравнений (всего шести) определяются значения n^αβ=n^βα, u_α и u.

Если решение системы (2.61)—(2.63) при заданных граничных условиях существует, то оно соответствует чистому изгибанию оболочки без растяжения. Более подробно этот вопрос изложен в работе [6]. Методику расчета легко объяснить на примере круговой нити при внутреннем давлении и ветровой нагрузке. В случае использования теории 1-го порядка из уравнений (2.53)—(2.56) получаем:


При заданной нагрузке р можно вычислить указанные интегралы; тогда усилие n_φ и перемещения u_φ и u определяются непосредственно в зависимости от постоянных интегрирования C₁,...,С₄, которые находят из четырех граничных условий для u_φ и u. Следует отметить, что постоянные интегрирования могут быть найдены лишь при определенной форме задания граничных условий; в рассматриваемом случае это легко сделать, если концы нити неподвижно закреплены. Не вдаваясь в подробности, заметим, что, например, для упрощенной теории цилиндрической мембраны 1-го порядка в форме (2.29)—(2.34) решение не существует, если мембрана неподвижно закреплена по четырем сторонам.

3. Нагрузки

3.1. Предварительные замечания. Применительно к воздухоопорным оболочкам не представляется возможным исследовать отдельно только ветровую нагрузку, поскольку одновременно с ней на оболочку действуют еще по крайней мере собственный вес и внутреннее давление, далее эти три вида нагрузок будут рассмотрены более подробно. Собственный вес оболочки в общем не играет существенной роли. Внутреннее давление можно надлежащим образом регулировать, устанавливая его в соответствии с условиями эксплуатации сооружения. Что касается ветровой нагрузки, то для ее назначения пока еще нет достаточно обоснованных данных. Ветровая нагрузка зависит от многих параметров, в том числе и от принятой величины внутреннего давления.

Кроме упомянутых выше нагрузок, на воздухоопорные оболочки могут действовать еще снеговая нагрузка и особые нагрузки (например, нагрузки от оборудования); однако в настоящей статье они не рассматриваются.

Ввиду многообразия возможных геометрических форм воздухоопорных оболочек мы ограничимся в дальнейшем рассмотрением типичных форм оболочек, показанных на рис. 1.

3.2. Собственный вес. Собственный вес оболочки g существенным образом определяется ее материалом. Для обычно применяемых в настоящее время пролетов оболочек и типов тканей собственный вес редко превышает 10 Н/м², что, как правило, пренебрежимо мало по сравнению с внутренним давлением и ветровой нагрузкой. Исключения возможны лишь при использовании весьма тяжелых тканей (в оболочках очень больших пролетов) либо при устройстве дополнительной теплоизоляции оболочек с целью экономии энергии [2]. В некоторых случаях необходимо учитывать также постоянные нагрузки от веса элементов оборудования, осветительных приборов и т. п. Прежде указывалось также на возможность повышения собственного веса оболочек вследствие намокания ткани; однако теперь, в связи с применением эффективных водоотталкивающих покрытий, этот вопрос потерял свое значение.

3.3. Внутреннее давление. Внутреннее избыточное давление воздуха p_i в сооружении создается обычно с помощью вентиляторов (воздуходувок). Внутреннее давление) не является строго неизменным в течение времени, поскольку постоянно происходит утечка воздуха из оболочки через разного рода неплотности, которую необходимо компенсировать. Поэтому следует различать номинальное и эксплуатационное внутреннее давление. Под номинальным понимают внутреннее давление, принимаемое в расчетах оболочек и регламентируемое соответствующими национальными нормами. Эксплуатационное (фактическое) давление воздуха, устанавливаемое в зависимости от изменения условий эксплуатации сооружения, может в большей или меньшей, степени отличаться от номинального. В особенности это относится к системам с автоматическим регулированием давления в зависимости от скорости ветра.

Внутреннее избыточное давление воздуха создает предварительное напряжение оболочки и тем самым обеспечивает несущую способность воздухоопорного сооружения в целом. Оно имеет решающее значение для стабильности формы и надежности сооружения, а также в значительной степени определяет напряженно-деформированное состояние оболочки. Внутреннее давление должно быть по меньшей мере достаточным для придания оболочке требуемой формы с учетом собственного веса. Необходимо, далее, чтобы при любых возможных нагрузках во всей оболочке действовали только растягивающие усилия, за исключением отдельных небольших участков — например, в местах анкеровки или в переходных областях между зонами различной кривизны. Значительное складкообразование и, тем более, «флаттер» (полоскание) оболочки должны быть, безусловно, исключены по соображениям надежности. При слишком малом внутреннем давлении возможны чрезмерно большие перемещения оболочки, которые могут привести к уменьшению полезного объема сооружения, а в отдельных случаях — к соприкасанию оболочки с находящимися под ней предметами и к разрушению материала оболочки. С другой стороны, слишком высокое внутреннее давление также невыгодно, поскольку это вызывает повышенный расход энергии и перенапряжение несущих элементов конструкции (оболочки и анкерных устройств).

Таким образом, для правильного выбора внутреннего давления следует руководствоваться требованиями как надежности, так и экономичности сооружения. Критерии для установления минимального и максимального внутреннего давления, а также рекомендации по назначению этой величины в обычных условиях эксплуатации приведены, в частности, в работе [9]. В работе [20] на основании результатов испытаний моделей рекомендуется принимать следующие отношения внутреннего давления к скоростному напору ветра (p_i/q):

• для полуцилиндрических оболочек (при h=r) — 0,62;
• для пологих цилиндрических оболочек (при h<r) — 0,50;
• для полусферических оболочек — 0,74.

При этих отношениях оболочка деформируется лишь в области положительного ветрового давления (напора). Аналогичные значения приведены в работах [5, 16, 27].

Следует вкратце отметить еще одну особенность. При ветровой нагрузке происходит деформация оболочки, вызывающая уменьшение объема сооружения. При этом, если температура и масса воздуха в объеме сооружения остаются неизменными, происходит повышение внутреннего давления, так как произведение объема на давление является константой. Влияние этого фактора, однако, невелико, поскольку максимальный скоростной напор ветра достигается лишь при коротких порывах (пульсациях). В работе [23] для трех исследованных случаев обнаружено повышение внутреннего давления от 2,3 до 6%, причем большее из этих значений соответствует пологой цилиндрической оболочке (относительно наиболее деформативной) с радиусом 18 м. Столь незначительным повышением внутреннего давления можно пренебречь в запас надежности.

3.4. Ветровая нагрузка. Ветровая нагрузка w, неравномерно распределенная по поверхности воздухоопорной оболочки, обычно представляется в форме ω=cq, где с — аэродинамический коэффициент (положительный при напоре и отрицательный при отсосе), q — скоростной напор ветра.

Скоростной напор q определяется скоростью ветра, обтекающего сооружение. Описание реального поля ветра, характеризующегося наличием турбулентных вихрей (порывов), будет, по-видимому, даже в обозримом будущем связано с введением ряда гипотез и упрощений. Поэтому в конкретных случаях при назначении расчетного скоростного напора ветра руководствуются соответствующими нормами и инструкциями. Для практических расчетов в общем достаточно учитывать лишь статическую составляющую скоростного напора, хотя, вообще говоря, он содержит также квазистатическую и динамическую составляющие.

Значения аэродинамического коэффициента с, характеризующего местное распределение ветровой нагрузки по поверхности сооружения, определяются для воздухоопорных оболочек пока только путем испытания моделей в аэродинамических трубах. Использование этих значений для описания реального нагружения натурных сооружений возможно лишь с учетом определенных факторов, подробно рассмотренных в соответствующей литературе [4, 5, 16, 20, 26]. Из них следует упомянуть влияние числа Рейнольдса; соблюдение закона подобия модели по материалу; тип модели (жесткая или гибкая); характер потока (ламинарный или турбулентный); форму вертикального профиля ветра.

Значение аэродинамического коэффициента зависит, кроме того, от направления потока ветра и от отношения внутреннего давления к скоростному напору. Почти совершенно не изучено влияние динамического характера ветровой нагрузки.

В связи с изложенным не следует ожидать, что распределение ветрового давления можно рассматривать как достаточно надежно обоснованную характеристику. В самом деле, даже опубликованные в литературе результаты измерений на моделях обнаруживают значительные расхождения. Подробное рассмотрение этой проблемы выходит за рамки настоящей статьи. Мы лишь ограничимся ссылкой на некоторые основные работы, содержащие результаты измерений на моделях оболочек следующих форм: полусфера — [4, 20];

• полуцилиндр со сферическими торцами — [16, 20, 26];
• полуцилиндр на прямоугольном плане — [5, 20];
• пологая цилиндрическая оболочка с закругленными торцами — [16];
• то же, на прямоугольном плане — [20].

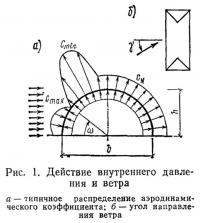
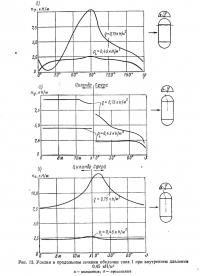
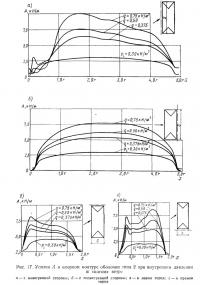
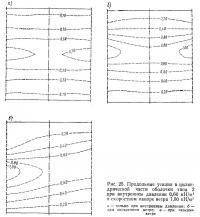
Для рассматриваемых в настоящей статье цилиндрических оболочек (более подробно их поведение при ветровой нагрузке обсуждается ниже) наблюдается следующая закономерность [20]. В верхней средней части оболочки распределение аэродинамического коэффициента соответствует показанному на рис. 1. Это распределение характеризуется тремя основными значениями коэффициента c:c_max (максимальное давление), c_min (максимальный отсос) и c_N (отсос «за потоком»), а также значением центрального угла ω для «нулевой» точки эпюры давления. Эти значения зависят от отношения внутреннего давления к скоростному напору p_i/q, направления ветра (угла γ), формы торцов оболочки и отношения высоты оболочки к ее радиусу h/r.

С увеличением отношения p_i/q центральный угол со незначительно уменьшается, т. е. сокращается размер зоны напора (например, для полуцилиндра ω=55° при p_i/q=0,4 и ω=45° при p_i/q=0,9). Интенсивность «пика» отсоса c_min оказывается несколько выше для оболочки с закругленными торцами, чем при прямоугольном плане (посередине длины оболочки при γ=30° значения c_min равны соответственно — 2,65 и —2,25). С уменьшением отношения h/r интенсивность отсоса также уменьшается (для оболочки на прямоугольном плане при γ=30° c_min=—2,25 при h/r= 1 и c_min=—1,90 при h/r=0,75). Приведенные выше значения заимствованы из работы [20], где установлено, что наиболее неблагоприятным является действие ветра на оболочку под углом у = 30°. Аналогичные результаты получены в работе [16], где исследовались цилиндрические оболочки со сферическими торцами при отношениях высоты к радиусу, равных 1,0 и, 0,65. В этой работе, однако, установлено, что наиболее неблагоприятным является действие ветра при γ=15°, а также получены другие, частично более высокие, значения интенсивности ветрового давления. При направлении ветра вдоль оболочки давление на ее поверхности оказывается значительно меньше по величине и распределяется более равномерно, без выраженных «пиков».

Распределение ветрового давления у торцов оболочки не подчиняется столь простым закономерностям; в общем можно лишь констатировать, что «пики» отсоса смещаются в подветренную сторону, а их интенсивность становится значительной.

Имеющиеся данные свидетельствуют о том, что на нынешнем уровне наших знаний не представляется возможным дать универсальные рекомендации по назначению ветровой нагрузки. Неизвестна функциональная зависимость распределения аэродинамических^ коэффициентов от таких факторов, как отношение внутреннего давления к скоростному напору, направление ветра, форма оболочки; поэтому невозможно и однозначное аналитическое описание такого распределения. Кроме того, ветровая нагрузка зависит еще и от перемещений оболочки, т. е. является неконсервативной. Таким образом, расчет воздухоопорной оболочки на ветровую нагрузку должен выполняться особо для каждого конкретного случая; распространять результаты этого расчета на иные условия следует с надлежащей тщательностью, имея в виду возможную потерю точности.

4. Свойства материала

Ткани, применяемые для воздухоопорных оболочек, отличаются весьма сложным механическим поведением. Наиболее распространены ткани с поливинилхлоридным покрытием (ПВХ); начинают применять также стеклоткани, покрытые тефлоном (ПТФЭ) [1]. Многообразие видов выпускаемых тканей с покрытием из ПВХ обусловливает различие их индивидуальных свойств, из которых здесь будут в общей форме рассмотрены лишь наиболее важные. Более детальные сведения можно найти в литературе [18, 19, 24, 25, 27].

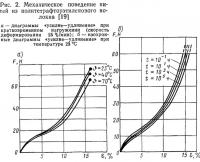
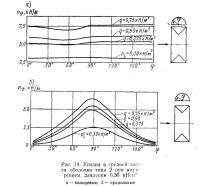
Механическое поведение отдельных нитей ткани при постоянной скорости деформации и различных температурах испытания показано на рис. 2, а; при длительном действии нагрузки и постоянной температуре — на рис. 2, б. Удлинения при длительной нагрузке с хорошим приближением выражаются линейной зависимостью от логарифма времени [19].

Механическое поведение ткани без покрытия в общем аналогично поведению отдельных нитей; различие свойств ткани по основе и утку определяется технологическим процессом ее изготовления. При этом полное удлинение ткани складывается из собственно удлинения и из вытяжки нитей, получивших искривление (волнистость) при изготовлении ткани; последний эффект сильнее проявляется при небольших нагрузках. Естественно, что удлинение ткани в направлении утка оказывается намного больше, чем вдоль основы, как видно на рис. 3. Ткань без покрытия практически не обладает жесткостью при сдвиге и характеризуется ярко выраженной ортотропией в направлениях основы и утка.

На рис. 3, а показаны диаграммы «усилие—удлинение» для ткани с покрытием (по основе и утку) при кратковременном испытании на одноосное растяжение [19]. Характер обеих кривых сходен с аналогичными зависимостями для отдельных нитей и для ткани покрытия. Влияние температуры также проявляется аналогично тому, как это имеет место для отдельных нитей (см. рис. 2, а) [19]. Влияние скорости деформации на механическое поведение ткани показано на рис. 3,6. Во всех случаях при кратковременном испытании на одноосное растяжение обнаруживается ярко выраженная физическая нелинейность материала; это остается справедливым и при двухосном растяжении, причем в данном случае характер кривых «уси-





-вильно, иногда в отдельных частях конструкции могут появиться вызванные несовершенством расчетной модели «белые пятна», которые следует надлежащим образом расшифровать, чтобы не прийти к ложным выводам из результатов расчета. При этом в отдельных случаях может оказаться необходимым произвести повторный расчет, если для наиболее напряженных частей конструкции получены слишком1 сомнительные данные. Этот вопрос рассмотрен более подробно в п. 6.4

В заключение кратко остановимся на весьма приближенных методах расчета, широко применявшихся в прошлом. При использовании этих методов воздухоопорная конструкция расчленяется на составные части (цилиндр, сферические торцы), каждая из которых рассчитывается отдельно: цилиндрическая часть — приближенно по теории нерастяжимой нити [23], сферические части — по линейной мембранной теории. При этом не выполняются условия совместности в переходных зонах оболочки, степень точности определения усилий и перемещений не поддается строгой оценке, а напряженное состояние оболочки в направлении образующих цилиндра вообще не может быть рассчитано. При наличии имеющейся в настоящее время вычислительной технику подобные грубые методы расчета уже непригодны, за редкими исключениями. Логично поэтому, что по нормам ФРГ [32] требуется производить расчеты пневматических оболочек по нелинейной теории, с учетом условий совместности.

6. Результаты расчета

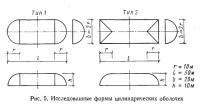
6.1. Исходные данные. Исследованы два типа конструкций, представленные на рис. 5: полуцилиндрические оболочки с полусферическими (тип 1) и полуцилиндрическими (тип 2) торцами; в обоих случаях принято b/l=0,40 и h/r=1,0. Основной целью проведенных расчетов была оценка различия в напряженно-деформированном состоянии оболочек с различным очертанием торцов.

Материал оболочек принят линейно-упругим, состоящим из двух слоев — ортотропной ткани и изотропного покрытия. Упругие характеристики слоев (модули упругости E и коэффициенты поперечной деформации v) приняты равными: для ткани E=108,4 кН/см² (по основе) и E=28,4 кН/см² (по утку), v=0; для покрытия E=11,6 кН/см²; v=0,45.

Численный расчет выполнялся в предположении совместной деформации слоев; толщина каждого из слоев принята равной 0,6 мм.

Значения указанных выше характеристик не «привязаны» к какому-либо конкретному материалу, а скорее типичны для целого класса применяемых на практике материалов, причем эти значения примерно соответствуют экспериментальным данным, приведенным в работе [24]. Ориентация ткани принята в расчете таким образом, чтобы нити основы располагались в кольцевом направлении, а нити утка — в продольном.

Собственный вес g оболочки в расчете не учитывался, поскольку его влияние в рассматриваемом случае весьма незначительно.

Среднее значение внутреннего давления р_i принято равным 0,30 кН/м²; для скоростного напора ветра q принято три значения — 0,375, 0,50 и 0,75 кН/м², что соответствует значениям отношения p_i/q, равным 0,8, 0,6 и 0,4. Для оболочки типа 2 были дополнительно проведены исследования еще при значениях внутреннего давления 0,45 и 0,60 кН/м² и соответствующих значениях p_i/q, так что всего было исследовано девять различных сочетаний нагрузок. Для оболочки типа 1 к настоящему моменту дополнительно исследовано сочетание p_i=0,45 кН/м² и q=0,75 кН/м², так что в данном случае общее число исследованных сочетаний нагрузок равно четырем. Сводка всех сочетаний нагрузок дана в табл. 1. Эти сочетания были приняты с таким расчетом, чтобы оценить влияние изменения интенсивности каждой из нагрузок p_i и q при неизменном отношении p_i/q, Значение скоростного напора ветра q было во всех случаях принято постоянным по высоте.


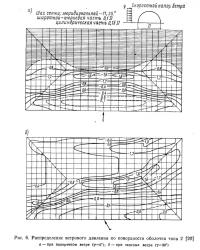
Распределение ветрового давления по поверхности оболочек было принято на основе результатов испытания моделей, приведенных в работе [20]. Соответствующие эпюры давления для оболочки типа 1 (при поперечном направлении ветра) приведены в работе [8], а для оболочки типа 2 (при поперечном и «косом» ветре, соответственно при γ=0 и γ=30°) показаны на рис. 6. Эти эпюры давления были приняты постоянными для всех сочетаний нагрузок, хотя в действительности они зависят также от отношения p_i/q.

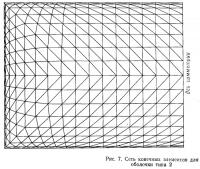
Все численные расчеты были выполнены по системе программ MESY [11]. При этом были использованы треугольные плоские конечные элементы («элементы постоянного удлинения»): для оболочки типа 1—1614 элементов с 849 узлами, для оболочки типа 2—1024 элемента с 561 узлом. Расчет на внутреннее давление и на поперечный ветер в силу симметрии системы был произведен только для одной половины сети конечных элементов. Сеть для оболочки типа 2 показана (в вертикальной проекции) на рис. 7.

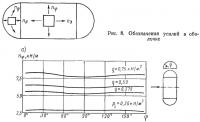
Подобное описание процедуры расчета по МКЭ можно найти в работах [8, 12], поэтому останавливаться на ней мы не будем. При расчете в качестве исходной была принята «идеальная» форма оболочки в соответствии с рис. 8; затем оболочка «нагружалась» внутренним давлением p_i и к полученной новой равновесной форме оболочки прикладывалась ветровая нагрузка полной расчетной интенсивности. Окончательная равновесная форма оболочки определялась путем итераций. Если по расчету в каком-либо конечном элементе появлялись сжимающие напряжения, то он рассматривался как ненапряженный и не передающий усилий. На каждом шаге итерационного процесса осуществлялась перепроверка напряженного состояния таких «холостых» элементов, и при изменении знака напряжения они вновь включались в систему. Рассчитанные таким образом значения усилий и перемещений частично приведены в двух последующих разделах; обозначения усилий показаны на рис. 8.

Все расчеты были выполнены на ЭВМ TR 440 вычислительного центра Рурского университета в Бохуме при участии дра-инж. Б. Хартмана, дра-инж. Х.-Ю. Нимана и инж. 3. Саналя. Анализ и графическая обработка результатов расчетов выполнены с помощью инж. Г. Брейцке и Дриллинга.

6.2. Типичное распределение усилий

6.2.1. Оболочка типа 1 при поперечном ветре. На рис. 9 показаны эпюры кольцевых усилий n_φ и продольных усилий n_v в средней части оболочки. Кольцевые усилия почти постоянны по сечению, что соответствует расчету по теории нерастяжимой нити. Совершенно иначе обстоит дело с продольными усилиями n_v. Если при внутреннем давлении р_i они почти постоянны по сечению, то при наложении ветровой нагрузки w эти усилия резко возрастают в верхней части оболочки и уменьшаются вблизи опорного контура. Изменение усилий имеет в общем достаточно плавный характер; это свидетельствует о том, что торцы мало влияют на напряженное состояние оболочки в ее средней части.

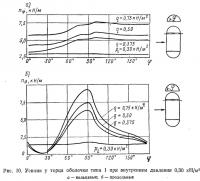
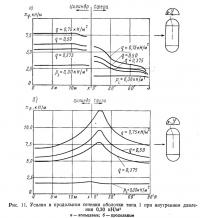
Влияние торцов четко обнаруживается на рис. 10, где показаны эпюры усилий на расстоянии около 2 м от торца. В этой зоне кольцевые усилия в общем уменьшаются, особенно с наветренной стороны, а продольные усилия в верхней части оболочки, наоборот, заметно возрастают; в целом распределение усилий становится значительно менее равномерным. Усилия n_φ и n_v от одного только внутреннего давления остаются практически неизменными. На напряженном состоянии оболочки у самой границы ее цилиндрической части, естественно, сильно сказывается влияние торца, как видно из рис. 11. Возрастание продольных усилий n_v в верхней части оболочки обусловлено значительным приростом усилий n_v в сферическом торце.

Что касается самого торца, то его напряженное состояние, если не считать локальных эффектов, типично для сферических оболочек: усилия n_v концентрируются в окрестности полюса, а усилия n_φ играют лишь второстепенную роль. «Скачок» в усилиях n_φ на рис. 11 является следствием изменения усилий, вызванного внутренним давлением. Приведенные рисунки соответствуют внутреннему давлению p_i=0,30 кН/м²; они опубликованы в работе [8]. Для полноты на рис. 12 и 13 приведены еще несколько эпюр усилий, рассчитанных при внутреннем давлении р_i=0,45 кН/м² и скоростном напоре ветра q=0,75 кН/м².

Рис. 12. Усилия у торца оболочки типа 1 при внутреннем давлении >

Рис. 13. Усилия в продольном сечении оболочки типа 1 при внутреннем давлении >

Рис. 14. Усилия в средней части оболочки типа 2 при внутреннем давлении >

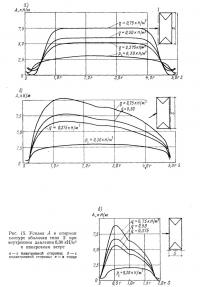
6.2.2. Оболочка типа 2 при поперечном ветре. Кольцевые и продольные усилия в средней части оболочки показаны на рис. 14. Их эпюры имеют плавный характер и аналогичны соответствующим эпюрам для оболочки типа 1 (см. рис. 9); различие имеется лишь в усилиях n_v от внутреннего давления. Усилия в опорном контуре показаны на рис. 15. В средней части длины оболочки они распределены очень равномерно и сильно убывают только у торцов. В этих местах появляются ненапряженные зоны оболочки, которые можно наблюдать и на моделях. Наибольшие по абсолютной величине усилия в опорном контуре действуют в торцах оболочки (рис. 15, в). Аналогичная картина усилий наблюдается и при более высоких значениях нагрузок р, и q.

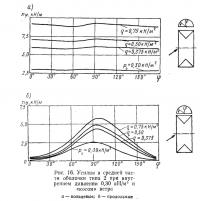
6.2.3. Оболочка типа 2 при «косом» ветре. Распределение усилий в оболочке типа 2 при «косом» ветре (рис. 16) в общем аналогично распределению усилий при поперечном ветре. При этом усилия n_φ заметно возрастают, а усилия n_v незначительно уменьшаются. Сильно возрастают также усилия в опорном контуре, причем максимума они достигают на подветренной стороне цилиндрической части оболочки. Усилия в опорном контуре торцов меньше по величине и сравнимы с усилиями от поперечного ветра (рис. 17).

6.2.4. Усилия от внутреннего давления. Для всех исследованных случаев были рассчитаны усилия в оболочках от одного только внутреннего давления. Если представить эти усилия в форме


Торцы оболочки типа 2 имеют переменный радиус кривизны. Для единообразия целесообразно отнести все усилия к постоянному радиусу цилиндрической части. Как видно из рис. 9—13, усилия n(p_i) и, следовательно, коэффициент β являются переменными величинами, хотя изменяются и не очень сильно.

6.2.5. Усилия от ветровой нагрузки. Как указано в начале раздела 6, усилия в оболочке могли быть рассчитаны только от ветровой нагрузки w в сочетании с внутренним давлением p_i.

Для определения усилий, вызываемых одной только ветровой нагрузкой, необходимо поэтому ввести некоторые допущения, обусловленные еще и тем, что ветровой нагрузке соответствует измененная геометрическая форма оболочки, для которой усилия от дополнительно приложенного внутреннего давления могут отличаться от усилий, вызываемых одним только внутренним давлением.


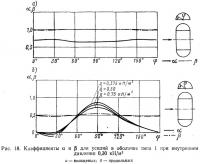
а также значения β:β_φ=1,00; β_v=0,54. Как видно, значения α_v сильно зависят от скоростного напора q; на значения α_φ он почти не влияет. То же относится и к соответствующим значениям n_φ и n_v. Полные эпюры коэффициентов аир для зоны оболочки, показанной на рис. 9, приведены на рис. 18; эпюры построены без учета слабой зависимости α_φ=f(q). Для обоих типов оболочек на основании рис. 9 и 11 может быть установлена следующая общая тенденция. В средней зоне цилиндрической части оболочки практически постоянно значение α_φ; вблизи торцов, наоборот, прекращается изменение значений n_φ. Там, где n_φ принимает наибольшее значение, α_φ почти постоянно и не зависит от q, а при малых значениях усилий эта зависимость, наоборот, выражена сильнее (аналогичная тенденция существует и в сферических торцах). Коэффициент α_v, в свою очередь, отличается значительной изменчивостью и зависит от скоростного напора q.

Описанный подход делает принципиально возможным определение усилий, вызываемых ветровой нагрузкой. Следует только иметь в виду, что вследствие принятых допущений о линейной суперпозиции усилий согласно выражению (6.3) и о доле усилия от р_i в суммарном усилии, полученные значения n(w) оказываются недостаточно надежными. В разд. 7 предлагается поэтому иной подход для расчета усилий n(w+p_i) по формуле (6.6).

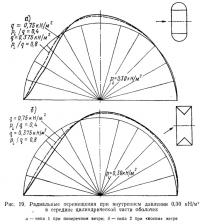
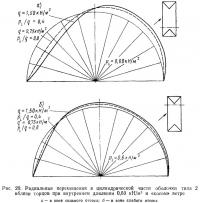
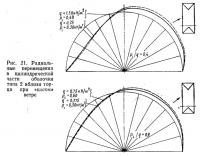
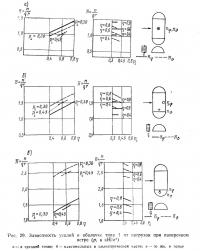
6.3. Типичное распределение перемещений. На.рис. 19 показаны радиальные перемещения в середине длины цилиндрической части оболочки при p_i=0,30 кН/м² и двух значениях скоростного напора ветра q:0,375 и 0,75 кН/м². При поперечном ветре эти перемещения практически одинаковы для оболочек типов 1 и 2. При «косом» ветре радиальные перемещения оболочки типа 2 больше с подветренной стороны и меньше в верхней части оболочки; с наветренной стороны они примерно одинаковы для обоих типов оболочек. Изменение радиальных перемещений по мере приближения к торцам показано на рис. 20 для оболочки типа 2 при «косом» ветре. Здесь хорошо обнаруживается влияние распределения ветрового давления (см. рис. 6, б): в области большего отсоса наблюдаются и значительно более высокие значения перемещений. Во всех случаях перемещения возрастают с увеличением скоростного напора q. Влияние интенсивности нагрузок видно из рис. 21.

При одном и том же отношении p_i/q большему внутреннему давлению (и, соответственно, большему ветровому напору) соответствуют более значительные перемещения; это увеличение, однако, существенно лишь с подветренной стороны оболочки.

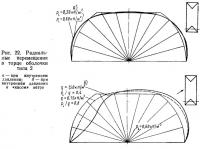
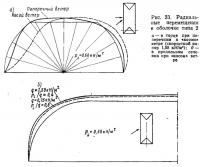
Интересно проследить за перемещениями в самих торцах оболочки. На рис. 22, а показаны радиальные перемещения примерно посередине торца от одного только внутреннего давления: средняя часть торца, первоначально прямолинейная, сильно искривляется. При дополнительном действии «косого» ветра в торце появляются значительные перемещения, величина которых сильно возрастает с увеличением ветрового напора (рис. 22, б). На рис. 23, а дано сравнение перемещений в торце оболочки при поперечном и «косом» ветре; на рис. 23, б показаны эпюры радиальных перемещений по длине среднего сечения оболочки типа 2.

Рис. 21. Радиальные перемещения в цилиндрической части оболочки типа 2 >

Рис. 22. Радиальные перемещения в торце оболочки типа 2 >

Рис. 23. Радиальные перемещения в оболочке типа 2 >

6.4. Анализ факторов, влияющих на напряженно-деформированное состояние оболочек

6.4.1. Влияние формы торцов при поперечном ветре. Как показывает сравнение рис. 9 и 14, в «невозмущенной» цилиндрической части оболочек усилия в кольцевом направлении в сущности одинаковы для обоих типов. Аналогичным образом обстоит дело и с усилиями n_v, хотя все же в оболочке типа 2 они распределены иначе, чем в оболочке типа 1, а их максимальное значение оказывается примерно вдвое больше. Эта общая закономерность сохраняется и в окрестности торцов. В самих торцах для оболочки типа 1 наблюдается значительный рост усилий n_v, тогда как усилия n_φ почти не изменяются. Сопоставление найденных из расчета максимальных значений усилий показывает, что в цилиндрической части оболочки типа 1 усилия т больше примерно на 7%, а усилия n_v — на 20%, чем для оболочки типа 2; соответственно в торцах усилия n_φ больше примерно на 20%, а усилия n_v — на 45%. Даже учитывая возможные погрешности численного расчета, можно констатировать, что в оболочке типа 1 действуют (при тех же нагрузках) более значительные усилия; в особенности это относится к усилиям Причина этого, наряду с различным распределением ветрового давления в оболочках типов 1 и 2, состоит в том, что в сферическом торце при ветровой нагрузке преобладающими являются меридиональные усилия, которые концентрируются в верхней части оболочки.

6.4.2. Влияние направления ветра при торцах, на прямоугольном плане. Различия в напряженно-деформированном состоянии оболочки типа 2 при поперечном и продольном ветре подробно проанализированы в работе [10]; ниже мы остановимся только на важнейших результатах. Из сравнения рис. 14, а и 16, а видно, что усилия n_φ в цилиндрической части оболочки оказываются значительно больше при «косом» ветре, что является прямым следствием более высоких значений ветрового отсоса (см. рис. 6). Усилия n_v, наоборот, остаются почти неизменными и даже несколько возрастают при поперечном ветре. Этот эффект обусловлен влиянием торцов, которые стабилизируют оболочку при поперечном ветре и тем самым полностью изменяют ее напряженно-деформированное состояние (см. рис. 23, а): главные напряжения действуют в верхней средней части оболочки под значительным углом к образующим, а в окрестности торцов — почти точно в направлении θ [10]. В работе [10] указано также на значительное уменьшение горизонтальных перемещений при поперечном ветре. Описанный эффект виден также на рис. 15 и 17: по продольным сторонам оболочки в опорном контуре действуют значительные усилия n_φ, и почти такие же по величине максимальные усилия действуют в опорном контуре по торцам (n_v). На этих рисунках также хорошо видны различия в изменчивости усилий n_φ и n_v при поперечном и продольном ветрах.

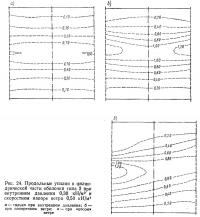
6.4.3. Влияние интенсивности нагрузок. Под изменением: интенсивности нагрузок мы будем понимать случай, когда отношение внутреннего напора к скоростному напору ветра p_i/q остается неизменным, а абсолютные значения p_i и q возрастают. Влияние интенсивности нагрузок ранее не было известно из литературы и впервые установлено на основании проведенных в настоящей работе численных расчетов. Это влияние четко обнаруживается по радиальным перемещениям оболочки (см. рис. 21). При том же отношении p_i/q более высокие нагрузки p_i и q вызывают и более значительные перемещения. В отношении усилий наблюдается обратная закономерность. На рис. 24 и 25 показаны (в безразмерном виде) продольные усилия n_v в цилиндрической части оболочки типа 2 при внутреннем давлении p_i, равном 0,30 и 0,60 кН/м², и постоянном отношении p_i/q=0,6. Указанное относительное снижение усилий с ростом нагрузки происходит уже при действии одного только внутреннего давления, причем оно особенно выражено в верхней части оболочки.

Здесь необходимо сделать четкое различие между усилиями и n_v. Как показывает анализ, выполненный в разд. 7, влияние интенсивности нагрузок особенно сильно сказывается на усилиях n_v; для усилий n_φ это влияние значительно меньше, а в «невозмущенной» средней зоне цилиндрической части оболочки им можно вообще пренебречь. Не вдаваясь в подробности, можно констатировать следующее. Усилия n_v в общем зависят от интенсивности нагрузки, рост которой приводит к относительному снижению этих усилий. Что касается усилий n_φ, то они по существу не зависят от интенсивности нагрузки; ее влияние обнаруживается лишь в небольших наиболее напряженных зонах цилиндрической части оболочки, а также в торцах. Причины этого явления следует искать в деформированном состоянии оболочки, особенно ее торцов, что как раз характерно для геометрически нелинейных систем. Как видно, например, из рис. 22, а, более высокому внутреннему давлению соответствует измененное геометрическое очертание оболочки; при приложении ветровых нагрузок напряженно-деформированное состояние оболочки снова изменяется. С ростом внутреннего давления возрастает, в частности, кривизна первоначально прямолинейных участков оболочки; при этом доля усилий n_φ в восприятии нагрузки увеличивается, а усилия n_v снижаются.

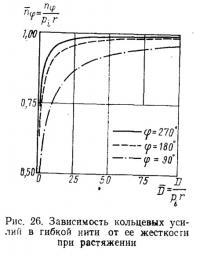
6.4.4. Влияние растяжимости оболочки. Все расчеты оболочек в настоящей работе выполнены при характеристиках материала, приведенных в разд. 6.1. Поскольку данные расчета при других характеристиках материала отсутствуют, точно установить их влияние на усилия и перемещения не представляется возможным. Для грубой оценки роли жесткости оболочки при растяжении был произведен параллельный расчет кольцевых усилий в оболочке по теории гибкой нити; для этого использована приведенная в п. 2.5 система уравнений упрощенной геометрически нелинейной теории круговой нити 1-го порядка. При действии внутреннего давления


решение этой системы находится в замкнутом виде. Кольцевое усилие определяется при этом из кубического уравнения


где φ — центральный угол раскрытия оболочки.

На рис. 26 показаны приведенные значения усилий n_φ=n_φ/p_ir в зависимости от приведенной жесткости оболочки D=D/p_ir для трех значений угла φ 90, 180 и 270°. С увеличением жесткости значения усилий n_φ приближаются к предельному значению, соответствующему нерастяжимой нити: n_φ=1 или n_φ=p_ir. Существенные отклонения от этого значения появляются лишь при малых значениях жесткости D и малых углах раскрытия φ. При значениях характеристик материала, приведенных в разделе 6.1, радиусе оболочки г=10 м и внутреннем давлении р_i=0,30 кН/м² приведенyая жесткость оболочки при растяжении равна D=246. Согласно рис. 26 при этом n_φ≈1,0 и n_φ≈3,0 кН/м (предельное значение для нерастяжимой нити). Только при достаточно больших значениях внутреннего давления p_i или радиуса оболочки r приведенная жесткость D возрастает настолько, чтобы можно было учитывать снижение усилия n_φ.

Интересно еще сравнить результаты расчета на основе теорий жесткой нити 1-го и 2-го порядка (см. раздел 2.5). При нагрузке вида (6.7) по теории 2-го порядка также получается замкнутое решение, причем усилие n_φ определяется из кубического уравнения


Таким образом, расчет на основе теории 2-го порядка приводит к меньшим усилиям (и большим перемещениям), причем различия с теорией 1-го порядка оказываются существенными, как и выше, при малых значениях жесткости оболочки при растяжении.

6.4.5. Влияние жесткости оболочки при сдвиге. Ткань, которая в исходном состоянии не сопротивляется перекосу, приобретает после нанесения покрытия некоторую жесткость при сдвиге. Точная оценка ее влияния на основании испытаний ткани на растяжение представляется проблематичной, как показывают результаты, приведенные в работах [16,24]. Поэтому в работе [15] были выполнены в параметрической форме расчеты оболочки типа 1 при поперечном ветре, в которых варьировались значения жесткости оболочки при сдвиге. При этом были приняты те же предпосылки, что и выше, а характеристики материала взяты из работы [24]. Схематично результаты расчета сводятся к следующему. С увеличением сдвиговой жесткости усилия n_φ в верхней средней части оболочки незначительно убывают, а вблизи торцов незначительно возрастают. Аналогичным образом изменяются усилия n_v, особенно в верхней части оболочки (здесь усилия снижаются почти на 50% при 16-кратном увеличении сдвиговой жесткости). В переходной зоне между цилиндрической частью оболочки и торцом усилия n_φ слабо возрастают в верхней части оболочки и незначительно убывают в направлении к опорам, а усилия n_v сильно возрастают в верхней части оболочки (примерно на 50% при 16-кратном увеличении сдвиговой жесткости). Эти результаты особенно важны, поскольку именно в оболочке типа 1 наблюдается значительная концентрация напряжений в верхней части у торцов (см. рис. 10 и 11). В этой зоне, в силу принятого раскроя, сгруппировано много швов, ужесточающих оболочку; в расчете такой эффект может быть учтен путем введения некоторой фиктивной сдвиговой жесткости. При этом как следствие возможно существенное перераспределение напряжений в оболочке, что оказывается важным о точки зрения ее экономичности и надежности.

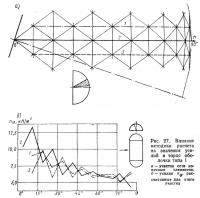
6.4.6. Влияние методики численного расчета. Как уже было отмечено в разд. 5, значения усилий в оболочке определенным образом зависят от самой методики расчета; там же были перечислены соответствующие факторы, специфичные для расчета на основе МКЭ. Влияние этих факторов особенно отчетливо обнаруживается в приведенных выше результатах расчета оболочки типа 1. Поясним это на примере усилий в торцевой части оболочки. На рис. 27 показаны участок сети конечных элементов и рассчитанные для этого участка усилия n_v. Отдельные значительные «скачки» усилий в смежных элементах не могут быть объяснены только локальной изменчивостью значений ветрового давления; скорее здесь играют существенную роль форма конечных элементов и конфигурация их сети. В действительности изменение усилий должно иметь более плавный характер, как показано на рис. 11,6. На погрешность такого рода при определении максимальных усилий n_v уже было указано выше.

Аналогичные эффекты, хотя и менее ярко выраженные, обнаруживаются и в других зонах оболочки типа 1, особенно при определении усилий в опорном контуре. Это наблюдение приводит к мысли, что причины погрешностей, подобных проиллюстрированным на рис. 27, кроются и в самой методике расчета. Ради полноты картины отметим, что для оболочки типа 2 подобных «скачков» в усилиях не наблюдалось, за исключением отдельных участков вблизи опорного контура (см. рис. 15 и 17).

7. Приближенные формулы для расчета основных усилии

7.1. Общие положения. Чтобы избежать необходимости вновь производить трудоемкие расчеты для каждого конкретного сооружения, представляется целесообразным получить приближенные формулы для определения основных усилий в оболочках. Это целесообразно еще и для сопоставления расчетных формул, принятых в различных странах. Для рассматриваемых здесь типичных форм оболочек будем считать справедливым линейное соотношение [см. (6.6)]


которое в такой форме приводится также в ряде национальных норм. Сопоставительный анализ, выполненный в работе [9], показывает, что значения коэффициентов α и β в общем могут быть приняты постоянными. При этом безразмерные значения усилий


оказываются линейно зависящими от отношения внутреннего давления к скоростному напору ветра


Справедливость этих допущений подтверждается приведенными выше численными результатами расчетов. При этом согласно разделу 6, усилия в кольцевом и меридиональном направлениях являются локально переменными и зависят от направления ветра, формы торцов оболочек и абсолютной интенсивности нагрузок.

Эти общие положения должны быть конкретизированы применительно к значениям коэффициентов α и β. Как было отмечено в п. 6.2.5, значения аир, входящие в формулу (7.2), будут здесь определены иначе, чем это было сделано в п. 6.2.5. Если там за основу было принято определение усилий n(w), то теперь мы будем представлять усилия n(w+p_i) в форме (7.2). Для этого используем следующую методику. Разделив суммарное усилие n(w+p_i) на qr, получим нормированную величину усилия n(w+p_i).

При этом каждому фиксированному значению p_i будут соответствовать три различных значения n(w+p_i) для различных значений скоростного напора (при η=p_i/Q=0,4; 0,6; 0,8). Указанные три значения n(w+p_i) могут быть аппроксимированы одной линейной зависимостью от η согласно (7.2). Тогда, например, на основе численных значений, приведенных в п. 6.2.5 для оболочки типа 1 с радиусом r=10 м, получим результаты, приведенные в табл. 2


Отсюда:

что с удовлетворительной точностью дает табличные значения (погрешность составляет около 1%).

Как показывает сравнение с данными п. 6.2.5, найденные таким образом значения β нельзя использовать, например, для определения усилий n(p_i) согласно выражению (6.1), так как там получено β_v=0 ,54, а здесь β_v=0,94. Однако преимущество использованной здесь методики заключается, в частности, в том, что нормированное суммарное усилие n(w+p_i) всегда может быть с достаточной точностью найдено из линейной зависимости (7.2) при фиксированных значениях α и β. В то же время при использовании методики, приведенной в п. 6.2.5, значение α_v, например, уже не было бы константой, либо погрешность при линеаризации согласно (7.2) оказалась бы чрезмерно большой.

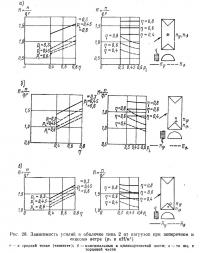
7.2. Полуцилиндрическая оболочка на прямоугольном плане. Рассмотрим вначале полуцилиндрическую оболочку с торцами на прямоугольном плане (типа 2). На рис. 28 и 29 приведены распределения основных усилий в оболочке для трех значений внутреннего давления p_i=0,30; 0,45; 0,60 кН/м² и для трех значений скоростного напора ветра (при η=0,4; 0,6; 0,8), при поперечном и «косом» ветре. Зависимость от η и p_i усилий в средней точке («зените») оболочки показана на рис. 28, а, максимальных усилий в цилиндрической части оболочки — на рис. 28, б и максимальных усилий в торце оболочки — на рис. 28, в. Усилия представлены в безразмерной форме согласно выражению (7.2). Общей для всех случаев является практически линейная зависимость усилий от отношения η=p_i/q. Усилия n_v зависят, кроме того, еще от внутреннего давления (или, эквивалентным образом, от скоростного напора ветра), что не наблюдается для кольцевых усилий. Значения усилий n_φ подчиняются линейным зависимостям (7.1) и (7.2) при постоянных значениях коэффициентов α и β и выражаются следующими формулами:


Возможны, разумеется, и другие формы представления усилий, где в качестве параметра может быть принято не внутреннее давление, а скоростной напор ветра.

Недостатком приведенных выше выражений является то, что они не являются безразмерными (здесь приняты размерности кН и м). Как отмечено в работе [10] и как поясняется в п. 6.4.4, в качестве параметра для приведения этих выражений (в том числе и для n_φ) к безразмерному виду удобно использовать нормированную жесткость оболочки при растяжении D=D/(p_ir).

Чтобы найти наиболее удобную форму представления усилий, необходимо выполнить еще значительное число расчетов и детальнее исследовать влияние различных факторов на напряженно-деформированное состояние оболочек. Поэтому пока что наиболее целесообразно пользоваться линейными приближениями, в том числе и для учета внутреннего давления. Если, например, принять, что внутреннее давление в оболочке не опускается ниже 0,30 кН/м², то для усилий n_v получим следующие выражения (с запасом):


Аналогичные линейные выражения получаются при р_i=0,45 и p_i=0,60 кН/м².

Обобщая приведенные результаты, можно записать следующие приближенные линейные выражения для максимальных усилий в цилиндрической и торцевой частях оболочки (эти усилия во всех случаях соответствуют «косому» ветру):


Отсюда могут быть приближенно определены и усилия n(w).

7.3. Полуцилиндрическая оболочка с торцами на круговом плане. Для данного типа оболочки к настоящему моменту получены результаты расчетов пока только для поперечного ветра и четырех сочетаний нагрузок: p_i=0,30 кН/м² при q=0,375; 0,50; 0,75 кН/м² и p_i=0,45 кН/м² при q=0,75 кН/м². Тем не менее даже на основании этих результатов уже можно сделать важные выводы, если обратиться к рис. 29 (который является неполным из-за недостатка численных данных). Усилия в цилиндрической части оболочки подчиняются тем же закономерностям, что и для оболочки с торцами на прямоугольном плане: они практически линейно зависят от отношения η= p_i/q, а усилия n_v — еще и от внутреннего давления. Полученную из расчета зависимость усилий n_φ в полусферическом торце от внутреннего давления нельзя считать вполне достоверной; здесь, по-видимому, играют определенную роль погрешности численного расчета, что отчасти разъясняется в п. 6.4.4. Таким образом, не следует переоценивать точность полученных значений усилий n_φ, особенно непосредственно в переходной зоне между цилиндрической и сферической частями оболочки. Видимые на рис. 29 «пики» в усилиях n_v также связаны с особенностями численного расчета; аналогичные эпюры усилий на рис. 11 «сглажены». На основе результатов расчета при p_i=0,30 кН/м² получены следующие линейные выражения для усилий:


Существенно отметить, что в приведенных уравнениях коэффициент при η везде близок к 1,0, тогда как во многих национальных нормах его значение принято равным примерно 0,5 (для усилий n_φ в торцах оболочки и для всех усилий n_v); этот результат объясняется принятой в п. 7.1 методикой определения усилий. Усилия в цилиндрической части оболочки не отличаются существенно от соответствующих усилий в оболочке с торцами на, прямоугольном плане, при том же поперечном направлении ветра. Несколько больше оказываются лишь максимальные значения усилий (вблизи торцов); в «невозмущенной» средней зоне оболочки значения усилий почти не меняются. Что же касается максимальных усилий n_v, они в данном случае имеют существенно более высокие значения — прямое следствие изменения формы торцов.

Для максимальных усилий при поперечном ветре и при p_i=0,30 кН/м² получены следующие приближенные линейные зависимости:


При «косом» ветре, по аналогии с оболочкой, имеющей торцы на прямоугольном плане, следует ожидать более высоких значений усилий.

Соответствующие усилия только от внутреннего давления определяются выражениями:


Отсюда могут быть также приближенно вычислены значения усилий n(w).

7.4. Сравнение с различными национальными нормами. Сопоставим значения усилий в оболочках, полученные из расчета численным методом и из приведенных выше приближенных линейных зависимостей, с соответствующими значениями, установленными в национальных нормах или инструкциях Великобритании [29], Японии [30], ГДР [31] и ФРГ [32].

7.4.1. Полу цилиндрическая оболочка с торцами на прямоугольном плане. Нормы Великобритании и Японии не содержат специальных указаний. Нормы ГДР (при 0,30≤h/d≤0,50):


Эти данные сведены в табл. 3. Усилия n_φ в цилиндрической части оболочки по нормам [31] слишком малы, в нормах [32] они определены довольно точно; усилия n_v, наоборот, слишком малы по нормам [32], особенно при небольших нагрузках p_i и q. Усилия n_φ и n_v в торцевой части оболочки по нормам [31} приняты равными и заметно завышены; в нормах [32], наоборот, слишком малы усилия n_φ. Сравнение при этом сделано с максимальными усилиями, которые соответствуют «косому» ветру и могут в отдельных случаях наблюдаться в действительности.


7.4.2. Полуцилиндрическая оболочка с торцами на круговом плане. Нормы Великобритании (при b/l=0,4 и h/r= 1,0):


Эти данные сведены в табл. 4. Как и в предыдущем случае, между данными различных национальных норм имеются заметные расхождения.

8. Заключение

Результаты проведенных исследований убедительно показывают, что расчет воздухоопорных оболочек все еще содержит множество «белых пятен». Следует надеяться, что благодаря проведению более интенсивных исследований на моделях и натурных испытаний в сочетании с развитием численных методов расчета показатели надежности воздухоопорных конструкций будут доведены до уровня, достигнутого для других конструкций.

Список литературы

• 1. Bird W. W. Teflon-coated fiberglas, an outstanding new material for fabric structures. Research report IASS Working Group of Pneumatic Structures, Yokohama National University, 1978, S. 2—18.
• 2. Bubner E. Zur konstruktiven Ausbildung der Warmedammung bei Bauwer-ken aus textilen Materialien. Membrankonstruktionen, Verlag R. Miiller, Koln, 1979, S. 21—48.
• 3. Bubner E. Zum Stand der Technik im Membranbau. Membrankonstruktionen 2, Verlag R. Muller, Koln, S. 17—24.
• 4. Gerhardt H. J. und C. Kramer. Traglufthallen unter aerodynamischer Belas-tung. Bauingenieur 51 (1976), S. 125—135.
• 5. Gerhardt H. J., C. Kramer und H. Jansen. Traglufthallen unter Windbelas-tung. Forschungsberichte des Landes Nordrhein—Westfalen, Nr. 2650, Westdeut-scher Verlag, Opladen, 1977.
• 6. Harnach R. Das Problem der verzerrungsfreien Verbiegung der Schalen-mittelflache aus differentialgeometrischer Sicht. Konstruktiver Ingenieurbau/Berich-te, Heft 20, Vulkan—Verlag, Essen, 1974, S. 5—34.
• 7. Harnach R. und W. B. Kratzig. Allgemeine Theorie geometrisch nichtlinea-rer, insbesondere leichter Flachentragwerke. Techn. — wiss. Mitteilungen Nr. 76—3 des Institute fiir Konstruktiven Ingenieurbau, Ruhr—Universitat Bochum, 1976.
• 8. Harnach R., B. Hartmann and H.-J. Niemann. Stresses and Deformations of Pneumatic Structures under Windload and internal pressure. Research report IASS-working group of pneumatic structures. Yokohama National University, 1978.
• 9. Harnach R. Vorschriften fiir Berechnung und Betrieb von Tragluftbauten. Membrankonstruktionen, Verlag R. Miiller, Koln, 1979, S. 105—126.
• 10. Harnach R. Load-carrying behavior of cylindrically shaped air supported structures. Acta Univ. Oul. С 16.1980, Artes Constr. 3, S. 579—590.
• 11. Hartmann В, К. H. Schrader und G. Winkel. MESY — Ein Programmsys-tem zur Untersuchung von Tragwerken. Konstr. Ingenieurbau/Berichte, Heft 22, Vulkan—Verlag Essen, 1975.
• 12. Hartmann B. and T. Drewes. On the numerical analysis of pneumatic structures, in Druck.
• 13. Haug E. und G. H. Powell. Finite element analysis of nonlinear membrane structures. Proc. 1971 IASS Pacific Symposium Part II on «Tension Structures and Space Frames», Tokyo and Kyoto, S. 165—175.
• 14. Haug E. und J. Oelbermann. Numerical design and analysis of pneumatic structures. CIB — International Symposium on air supported structures, Venedig, 1977.
• 15. Hockeler A. und J. Oelbermann. Numerische Parameterstudien an einer luftgetragenen Halle mit Hilfe der Methode der Finiten Elemente-Forschungsbe-richt. Formfindung vorgespannter Membrankonstruktionen, Essen, 1979.
• 16. Horde M. Windbelastung und Berechnung des Spannungs- und Verfor-mungszustandes im zylindrischen Teil von Traglufthallen mit besonderer Berfick-sichtigung des Konstruktionsmaterials. Diss. ETH Zfirich, 1974.
• 17. Koenen R. und E. Luksch. Untersuchungen und Oberlegungen zu Abschlufi-geometrien luftgetragener Hallen mit zylindrischem Mittelteil. Membrankonstruktionen 2, Verlag R. Muller, Koln 1980, S. 25—40.
• 18. Krummheuer W. Mechanical properties of PVC-coated polyester fabrics and their joints. Research report IASS Working Group of Pneumatic Structures, Yokohama National University, 1978, S. 28—37.
• 19. Meffert B. Mechanische Eigenschaften PVC-bescichteter Polyestergewebe. Dissertation, Aachen, 1978.
• 20. Niemann H.-J. Zur Windbelastung von Tragluftbauten. Konstruktiver Ingenieurbau/Berichte, Heft 13, Vulkan-Verlag, Essen, 1972.
• 21. Oelbermann J. Ausfiihrung und Berechnung von luftgetragenen Hallen nach der geplanten DIN 4134 und nach der Methode der Finiten Elemente. Membrankonstruktionen, Verlag R. Miiller, Koln, 1979, S. 87—104.
• 22. Otto F. Zugbeanspruchte Konstruktionen. Vol. 1, Ullstein-Fachverlag, Frankfurt/Berlin, 1962.
• 23. Petersen Ch. Zur Sicherheit von Traglufthallen. Bauingenieur 50 (1975), S. 117—123.
• 24. Rehm G. und R. Munsch. Zum Spannungs-Dehnungs-Verhalten im Geb-rauchslastbereich und zum Bruchverhalten von PVC-beschichteten Polyestergewe-ben. Symposium Weitgespannte Flachentragwerke, V'ol. 1, Stuttgart, 1979.
• 25. Rehm G. und R. Munsch. Zweiachsige Langzeit—Zugversuche an PVC— beschichteten Polyestergeweben. Symposium Weitgespannte Flachentragwerke, Vol. 1, Stuttgart, 1979.
• 26. Rontsch G. und F. Bohme. Modellstatische Untersuchungen fur eine als Halbzylinder mit Viertelkugelabschiissen ausgebildele Traglufthiille. Wiss. Zeitschr. Hochschule fur Verkehrswesen Dresden, 17 (1968), S. 183—189.
• 27. Schulz H. Die Konstruktion und Berechnung von Membrantragwerken. Bautechnik 54 (1977), S. 242—249 und 281—283.
• 28. Spinelli P. Windeffects on a cylindrical air supported structure. Proc. 3 rd Colloquium on Industrial Aerodynamics, Aachen 1978, S. 179—193.
• 29. DD50: 1976. Dratt for Development, air supported structures, Grofibritan-nien, 1976.
• 30. Pneumatic Structure Design Standard and Commentary, Japan, 1970.
• 31. TGL 10728/03, Traglufthallen, Deutsche Demokratische Republik, 1976.
• 32. DIN 4134, Tragluftbauten: Berechnung, Ausfiihrung und Betrieb, Bundes-republik Deutschland (Bearbeitungsstand Juli 1980).