Техническая теория мягких оболочек и ее применение для расчета пневматических конструкций

Теория мягких оболочек занимает важное место в механике деформируемого твердого тела и имеет много практических приложений.. Работоспособность различных типов мягких конструкций, применяемых в судостроении, машиностроении, воздухоплавании и космической технике, определяется в значительной степени теоретическим анализом. Особое место занимает теория при создании пневматических строительных конструкций. Проблемы не только прочности и деформативности, но также долговечности и эксплуатации конструкции решаются с помощью теории мягких оболочек.

Современные тенденции развития теоретических исследований связаны с дальнейшим расширением свойств как частных, так и общих моделей путем учета новых явлений, новых факторов, позволяющих более полно отразить поведение объекта. До недавнего времени расчет конструкций из мягких оболочек основывался на линейной безмоментной теории. В рамках этой схемы в большинстве случаев не удавалось определить деформированную форму оболочки и учесть влияние изменения геометрии на напряженное состояние.

Наиболее полное описание поведения конструкций связано с теорией больших деформаций мягких оболочек, учитывающей нелинейность характеристик материала и справедливой при перемещениях и деформациях, не ограниченных по величине. Вопросы теории больших деформаций мягких оболочек в различных вариантах разрабатывались в работах [1—3]. Общая система уравнений мягкой оболочки произвольной геометрий при больших деформациях и перемещениях получена в работе [4].

Однако расчетные схемы, в которых используются строгие теории при проведении практических расчетов, оказываются в большинстве случаев весьма сложными. Многие конструкции, кроме того, работают в условиях, при которых большие деформации и большие изменения геометрии недопустимы. К ним, в частности, относится большинство пневматических строительных конструкций.

Наиболее приемлемой при расчетах оказывается приближенная, так называемая техническая теория мягких оболочек, справедливая при малых деформациях и использующая линеаризацию при составлении системы уравнений.


Основная идея технической теории состоит в том, что усилия, действующие в оболочке в деформированном состоянии, представляются в виде суммы основных и дополнительных слагаемых. Первые члены соответствуют безмоментной теории оболочек и определяются из уравнений равновесия, записанных для начальной (раскройной) или некоторой промежуточной формы оболочки, которая считается известной. Дополнительные усилия корректируют значения основных членов. Они отражают влияние изменения геометрии оболочки на ее напряженное состояние. На тех участках оболочки, где изменения геометрии при деформировании невелики, величины дополнительных слагаемых малы. Дополнительные усилия могут быть определены при решении задачи только из полной системы уравнений.ЛЛинеаризация уравнений равновесия проводится относительно состояния оболочки, соответствующего начальной форме, и усилий, определенных для нее. Таким же образом упрощается выражение для полной потенциальной энергии оболочки, которое применяется при решении задач вариационными методами.

Техническая теория — наиболее простой вариант теории мягких оболочек. Являясь как бы первым приближением общей теории, она в то же время учитывает наиболее существенные свойства мягких оболочек и позволяет получить весьма достоверные решения .многих практически важных проблем. На ее основе в настоящее время построен ряд алгоритмов, созданы и широко используются программы расчета сложных конструкций.

1. Основные уравнения общей теории

Остановимся кратко на уравнениях теории больших деформаций. Следуя обозначениям работы [4], положим, что недеформированная геометрия оболочки определяется линиями главных кривизн α и β, коэффициентами первой квадратичной формы А, В и главными радиусами кривизны R₁, R₂.

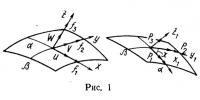
По касательной к линиям α и β (рис. 1) проведены оси х и у, которые вместе с направленной вдоль внешней нормали осью z образуют правый подвижный трехгранник. На деформированной поверхности оси х₁ и y₁ касательные к линиям α и β пересекаются под углом χ. Нормаль к плоскости х₁ и y₁ соответствует оси z₁. Вектор полного перемещения точки поверхности на оси xyz имеет составляющие u, v, w:



Удлинения линейных элементов, отнесенные к начальным размерам вдоль линий α и β, равны соответственно е₁ и е₂, косинус угла между осями х₁ и у₁ равен cosχ=ω.

Полные нелинейные соотношения между е₁, е₂, ω и перемещениями приведены в статье [4]:


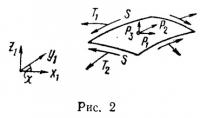
По граням элемента деформированной оболочки (рис. 2) действуют усилия Т₁, Т₂, S. Касательные усилия вдоль линий α и β равны между собой.

Условие равновесия элемента оболочки согласно принципу возможных перемещений имеет вид


Каждый член матрицы — направляющий косинус (1.6). Соотношение (1.10) позволяет выразить вектор {р} через {f}:



Подставим в вариационное уравнение (1.7) зависимости (1.8), (1.9), (1.2). Использование формул Остроградского—Гаусса для криволинейных координат позволяет получить уравнения равновесия и естественные граничные условия. Скалярная форма уравнений равновесия имеет следующий вид:


Уравнения равновесия (1.11)—(1.13) записаны для ортогональных осей х, у, z, которые направлены вдоль координатных линий, проведенных на недеформированной поверхности оболочки, и по нормали.

Построим систему силовых граничных условий для оболочки. Если рассмотреть только край оболочки, совпадающий с линией β (α=const), то из вариационных соотношений (1.7)—(1.9) получаются силовые граничные условия, которые представляются в виде


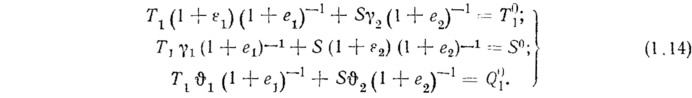
Первые два соотношения соответствуют равенству внутренних и краевых сил, направленных вдоль осей х и у. Третье уравнение показывает, что усилие, приложенное по нормали к начальной поверхности оболочки, деформирует ее так, что уравновешивание осуществляется только проекциями сил Т₁ и S.


Полученные зависимости должны быть дополнены уравнениями, отражающими свойства материала, из которого изготовлена оболочка. Эти уравнения могут иметь различную форму. Их выводят по результатам экспериментов или на основе теоретических соображений, но связь между усилиями и деформациями должна быть в рассматриваемой постановке однозначной.

2. Условия образования складок

Система уравнений, полученная выше, справедлива для мягких оболочек, находящихся в двухосном напряженном состоянии. При определенных условиях на поверхности оболочки или в отдельных ее зонах могут появиться складки, что является результатом возникновения сжимающих усилий. Оболочка как бы теряет устойчивость от усилий, действующих перпендикулярно направлению складок. Эти усилия малы по величине и при расчете принимаются равными нулю [1]. Считается, что такая зона образуется системой нитей, направление которых совпадает с положением главных растягивающих усилий.

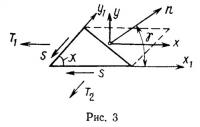
Получим условия образования складчатых участков. Рассмотрим треугольный элемент поверхности, который вырезан из четырехугольника (рис. 3), соответствующего деформированному состоянию оболочки. Вдоль граней x₁ и у₁ в косоугольной системе координат действуют силы Т₁, S и T₂, S. Приложим к третьей стороне треугольника усилия X и У так, чтобы вектор X совпадал с направлением x₁ а Y был перпендикулярен ему. Нормаль к этой стороне треугольника составляет с осью x₁ угол γ. Спроектируем все силы, действующие на элемент, на направления векторов X и У:


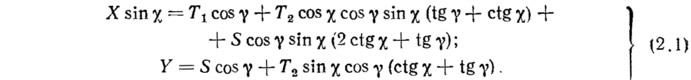
Найдем такие значения углов γ, при которых касательные составляющие вдоль линии ab отсутствуют. Если обозначить нормальную составляющую а, то в этом случае X и Y равны



Подставив эти соотношения в выражение (2.1), получим главные усилия в виде


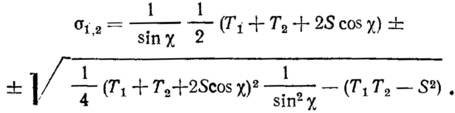
Знак плюс в этом уравнении соответствует большему главному усилию. При возникновении складок меньшее главное усилие должно быть равно нулю. Отсюда следует условие образования складок


Если левая часть уравнения больше нуля, то складки в этой зоне оболочки отсутствуют.

Направление складок может быть определено из уравнения (2.1). Когда σ=0, угол γ находится из соотношения


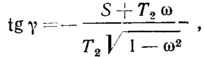
где ω = cos χ.

3. Общие уравнения технической теории

Далее на основе приведенных строгих соотношений теории мягких оболочек построены уравнения технической теории. При малых деформациях значения ε, γ и θ соответствуют относительному удлинению, составляющей угла сдвига и углу поворота нормали к поверхности оболочки. Следовательно, соотношениями (1.4) определяются зависимости между векторами деформаций и вектором перемещений.

Усилия, действующие в оболочке, представляются в виде сумм


Первые слагаемые отнесены к начальной форме и считается, что они находятся из уравнений равновесия безмоментной теории оболочек при поверхностных нагрузках f₁₀; f₂₀; f₃₀.

Полные составляющие поверхностных нагрузок также разделяются на две части:


Усилия T₁₀, Т₂₀, S₀ и нагрузки f₁₀; f₂₀; f₃₀ соответствуют состоянию оболочки, называемому основным. Разделение внешней нагрузки удобнее всего проводить так, чтобы первые слагаемые в выражении (3.1) описывались плавно изменяющимися функциями. В этом случае решение задачи для определения основного напряженного состояния будет наиболее простым. Нужно отметить, что разделение поверхностных внешних усилий (3.1) не обязательно. Во многих случаях можно относить всю внешнюю нагрузку к основному состоянию.

Рассмотрим условие равновесия мягкой оболочки (1.7). Воспользовавшись разделением усилий (3.1), представим их работу на возможных перемещениях в виде трех слагаемых


Первое слагаемое соответствует работе сил основного состояния или, иначе, безмоментной теории оболочек:


В выражении для δV₁ будем учитывать лишь деформации и углы поворота, умноженные на усилия основного состояния, а также дополнительные усилия


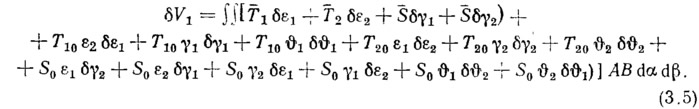
Именно составляющая работы внутренних сил δV₁ занимает основное место в технической теории мягких оболочек. Она позволяет значительно расширить возможности безмоментной теории и получить непротиворечивые решения. В выражение для δV₂ входят члены, которые при малых значениях деформаций незначительны и в технической теории мягких оболочек не учитываются.

Работа поверхностной нагрузки на возможных перемещениях определяется первым слагаемым соотношения (1.9). Представим ее также в виде трех слагаемых


В соответствии с разделением поверхностных сил на основные и дополнительные работу основных сил представим в виде


Слагаемое δП₁ получено в результате линеаризации первого слагаемого подынтегрального выражения (1.9):


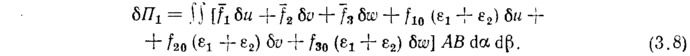
Третий член в выражении (3.6) соответствует нелинейным составляющим работы внешних сил и здесь не учитывается.

Работу краевых сил также будем рассматривать состоящей из трех слагаемых: основного, дополнительного и остаточного члена, определяемого нелинейными составляющими деформаций:


Каждую составляющую правой части можно найти, если разделить краевую нагрузку на основную и дополнительную.

Условие равновесия (1.7) теперь можно рассматривать раздельно:


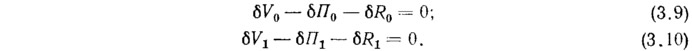
Первое соотношение относится к основному состоянию и соответствует линейной безмоментной теории. Второе является главным при построении линеаризованных соотношений технической теории мягких оболочек.

Воспользуемся зависимостями Остроградского—Гаусса и получим из соотношений (1.7), (3.5), (3.8) уравнения равновесия оболочки в криволинейных координатах и граничные условия. Заметим, что те же уравнения можно получить, если провести прямую линеаризацию полных зависимостей (1.11) — (1.13):


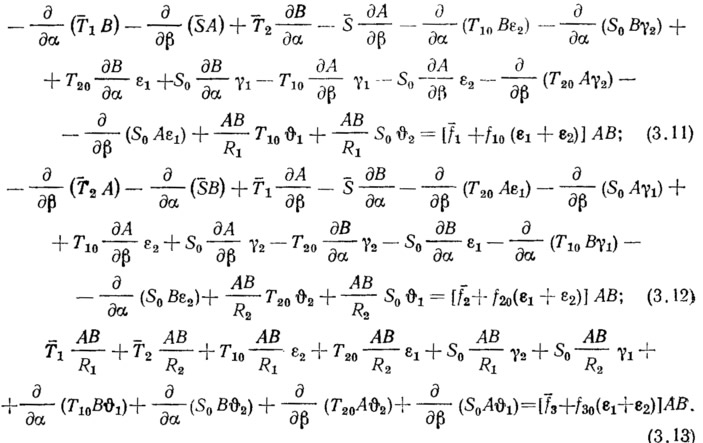
Правые части этих уравнений могут быть представлены иначе — через составляющие поверхностной нагрузки в координатах х₁, y₁, z₁ на деформированной поверхности. Используя соотношения (1.10), (1.6) и разделив аналогично выражению (3.2) полные поверхностные усилия на основные и дополнительные


в правых частях уравнений (3.11)—(3.13) получим:


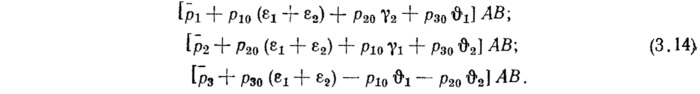
Поверхностные силы p₁₀, p₂₀, p₃₀ здесь определяют усилия Т₁₀, Т₂₀, S₀ основного состояния. Эти соотношения удобнее применять, например, при рассмотрении гидростатического нагружения оболочки или действия равномерного давления при расчете пневматических конструкций. При наличии только давления правые части уравнений имеют вид


Остальные слагаемые равны нулю.

Матричную форму уравнений равновесия при правых частях (3.14), поделенных на АВ, можно представить в виде


Здесь введены векторы

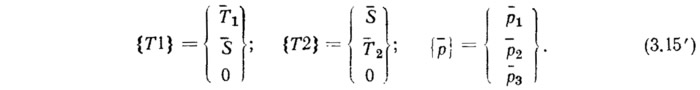
Первые два слагаемых соответствуют уравнениям равновесия безмоментной теории оболочек, матрицы [L1] и [L2] равны


Остальные члены левой части уравнения отражают влияние изменения геометрии на напряженное состояние.

Усилия основного состояния Т₁₀, Т₂₀, S₀ находятся из системы уравнений равновесия безмоментной теории оболочек:


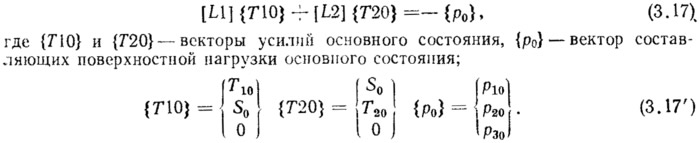
Если правые части уравнений (3.11)—(3.13) представить в виде (3.14), то в матричной форме их молено записать следующим образом:


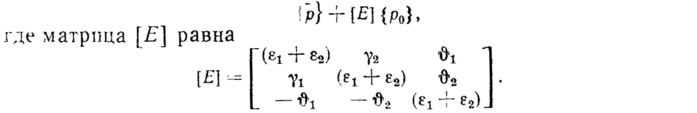
Подставив вместо вектора {р₀} из уравнения (3.17) усилия основного состояния, перенесем эти слагаемые в левую часть уравнения (3.15). Они, как видно, влияют только на третье и четвертое слагаемые левой части. В правой части уравнения останется только вектор дополнительной нагрузки. Матрицы [L3] и [L4] уравнения (3.15) приведены в приложении. Уравнения, связывающие внутренние усилия с компонентами деформации в технической теории, линейны. Для анизотропного упругого тела они имеют вид


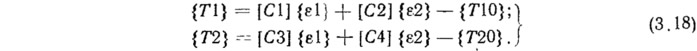
Матрицы упругих констант равны:

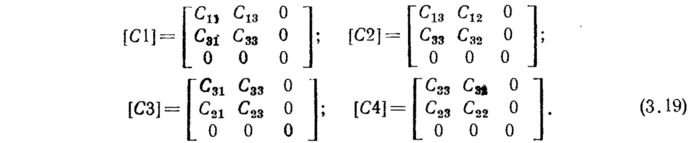
Каждая составляющая этих матриц включает не только коэффициент упругости, но и дополнительные члены, получаемые в результате линеаризации полных нелинейных зависимостей, в которые входят усилия основного состояния. При малых значениях деформаций усилия основного состояния, как правило, малы по сравнению с характеристиками жесткости материала и в расчетах могут не учитываться.


Кроме того, возможны разные комбинации силовых и геометрических условий. При решении задач этими условиями удобнее оперировать, когда они записаны в матричной форме:


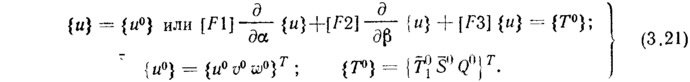
Матрицы [F1], [F2], [S3] приведены в приложении.

Полная система уравнений технической теории мягких оболочек имеет следующий вид:


Полученные уравнения в представленном виде могут быть решены лишь с использованием дискретных методов и ЭЦВМ. В различных частных случаях возможно упрощение приведенной системы.

4. Оболочка вращения

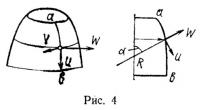
Для оболочки вращения общая система уравнений упрощается. Полагая, что α — угловая координата, определяющая точку на меридиане поверхности вращения, а β — положение самого меридиана (рис. 4), а также имея в виду, что коэффициенты первой квадратичной формы не зависят от β и равны A=R₁; В=r, матрицы геометрических соотношений и уравнений равновесия можно привести к простому виду (см. приложение). Матрицы упругих констант при этом остаются прежними. Общие соотношения технической теории мягких оболочек приведены в работе [5].

Решение задач для замкнутой по полярной координате оболочки ведется с помощью метода разделения переменных. Все компоненты перемещений, деформаций и усилий, а также составляющие поверхностной и краевой нагрузки представляются в виде суммы произведений двух функций, одна из которых периодическая по β. Перемещения принимаются в следующем виде:


Представление перемещений в виде (4.1) и аналогичная форма соотношений для усилий и деформаций позволяет рассматривать двумерную задачу теории оболочек как квазиодномерную. Можно отдельно получить решение для каждого m и затем, суммируя результаты, определить перемещения и усилия в оболочке при самых разных видах несимметричной нагрузки и условиях на граничных контурах.

5. Цилиндрическая оболочка (осесимметричный случай)

Для цилиндрической оболочки удается получить аналитические решения для перемещений и усилий при некоторых видах нагрузки. Здесь наиболее просто можно оценить значения различных слагаемых в общей системе уравнений. Эта оценка позволяет распространить решения для цилиндрической оболочки на оболочки более общего вида. Имея в виду, что R₁dα = dx, 1/R₁ = 0; α = π/2, r=R, из полной системы уравнений придем к упрощенным зависимостям. Рассмотрим вначале осесимметричный случай. Геометрические зависимости (1.4) принимают вид


Уравнения (5.5) показывают, что из всех слагаемых учитываются лишь те, которые содержат дополнительные усилия, а также усилие основного состояния, умноженное на старшую производную от нормального перемещения. Подобные упрощения могут быть использованы и при рассмотрении осесимметричных случаев деформирования не только цилиндрических оболочек. Однако неучет таких же членов без дополнительного обоснования в других задачах, как будет показано ниже, может привести к ошибочному решению. Исключая из системы (5.5) перемещение u, получим


Она мала по величине, и ее отношение к радиусу оболочки примерно пропорционально корню квадратному из величины продольной деформации. Решение (5.8) позволяет построить деформированную форму и найти усилия в оболочке при различных граничных условиях.

6. Краевой эффект

Приближение типа краевого эффекта широко используется при построении упрощенных решений моментной теории оболочек. Подобные упрощения можно провести при анализе уравнений (4.4), (4.5) мягкой оболочки вращения. Рассмотрим непологий участок оболочки. Будем считать, что размеры, краевой зоны невелики, так что кривизны в ее пределах можно считать постоянными. Положим также, что касательные перемещения меньше нормальных и производные от перемещения w больше самого перемещения. Эти предположения позволяют в случае осесимметричной деформации прийти к уравнению краевого эффекта мягкой оболочки [6]:


Коэффициент λ² считается постоянным. При малых деформациях он представляет собой большую величину. Без учета возрастающих функций решение этого уравнения вблизи края α=α₀ имеет вид


Полное нормальное перемещение в оболочке определяется двумя слагаемыми:


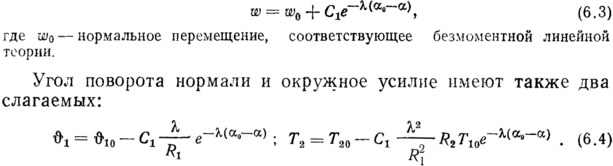
Меридиональное усилие Т₁ и касательное перемещение и в теории краевого эффекта определяются только безмоментным решением. Константа С₁ определяется из условий на границе оболочки.

7. Деформация цилиндрической оболочки при изгибе

При рассмотрении осесимметричного нагружения цилиндрической оболочки было показано, что все члены, содержащие усилия основного состояния, умноженные на линейные и угловые составляющие деформаций, за исключением одного, малы по величине и их можно не учитывать. Исключение относится к слагаемому, соответствующему усилию T₁₀, умноженному на старшую производную от перемещения w. На примере изгиба длинной цилиндрической оболочки, нагруженной внутренним давлением, покажем, что пренебрежение слагаемыми, не учитываемыми при осесимметричном случае, может привести к ошибочным результатам.

Линеаризованные уравнения равновесия для цилиндрической оболочки при m=1 принимают вид


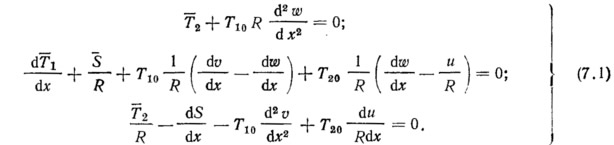
Продифференцируем второе уравнение по х, умножим на R и сложим с третьим. Вместе с первым уравнением получим систему


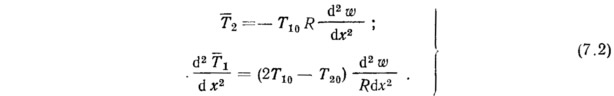
Эти соотношения получены без каких-либо дополнительных упрощений. Отметим, что все слагаемые здесь имеют примерно один и тот же порядок. Если, например, пренебречь во втором и третьем уравнениях (7.1) слагаемыми, содержащими усилия основного состояния, умноженные на компоненты перемещения и их производные, то вместо второго уравнения (7.2) получим


Использование в дальнейшем этого соотношения приводит к ошибочным результатам.

Для получения решения далее необходимо воспользоваться геометрическими и физическими соотношениями. Для изотропной оболочки при T10<<E_h; T₂₀<<E_h разрешающее уравнение принимает вид


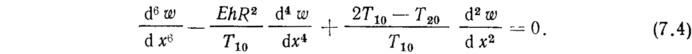
Решение этого уравнения в случае (2Т₁₀≠Т₂₀) состоит из четырех частных решений, соответствующих задаче для балки, и двух — краевому эффекту. Таким образом, мягкая оболочка, нагруженная равномерным давлением и изгибающим моментом, приложенным к торцевым сечениям, деформируется как балка. К балочному решению при определении деформированной формы оболочки необходимо добавить решение краевого эффекта с показателем изменяемости таким же, как и при осесимметричной деформации. Равномерное давление не создает изгибающего момента относительно центра сечения. Этот достаточно очевидный вывод, полученный из полных без упрощений линеаризованных уравнений, следует и из закона Паскаля.

Приведенный пример показывает, что при составлении уравнений нужно весьма осторожно прибегать к упрощениям, особенно когда деформированное состояние описывается не быстро изменяющимися функциями. Это относится не только к цилиндрической оболочке, но и к оболочкам других конфигураций.

8. Несимметричная деформация цилиндрической мягкой оболочки

В случае нагружения оболочки усилиями, изменяемость которых вдоль окружности значительна, деформированное состояние хорошо описывается приближенной теорией. К упрощениям, которые принимают при линеаризации уравнений, добавляют предположения, используемые в известной полубезмоментной теории цилиндрической оболочки. Имеются в виду равенство нулю числа Пуассона и зависимости


Исключая отсюда перемещение v и используя соотношение между осевым усилием и перемещением T₁=Ehdu/dx, получаем уравнения совместности деформаций


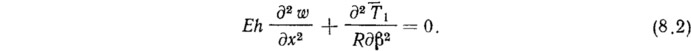
В уравнениях равновесия оставляют лишь дополнительные усилия и наибольшее по величине слагаемое при большой изменяемости функций по β. Заметим, что такого же типа слагаемое учтено при построении теории краевого эффекта, но со старшей производной по х:


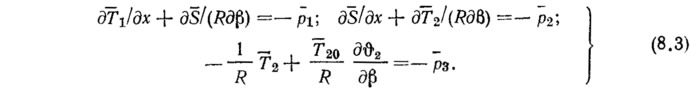
Таким образом, для определенного вида нагрузок принимают свои упрощения, но в каждом случае должны быть учтены наиболее существенные члены, соответствующие наибольшей изменяемости функций. Система (8.3) эквивалентна одному уравнению, связывающему осевое усилие с нормальным перемещением:


Константы C_1m—С_4m в уравнении (8.8) определяются из граничных условий на торцах оболочки.

Рассмотрим пример расчета цилиндра, нагруженного внутренним давлением и радиальной силой q, распределенной вдоль образующей. Оболочка имеет на торцах диафрагмы, жесткие в плоскости поперечного сечения. Осевые усилия на торцах равны Т₁₀. Разложив нагрузку в ряд, получим


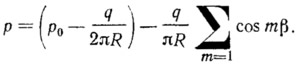
К нагрузке основного состояния отнесем слагаемое в круглых скобках. Если поместить начало отсчета по х посередине оболочки, то в решении (8.8) можно оставить лишь четные функции. Из условий x=l, w=0 и w"=0 (второе условие следует из того, что на торце дополнительное усилие равно нулю) определим константы С_1m, С_4m и нормальное перемещение w_m.

Перемещение w_m при х=0 равно


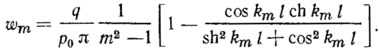
При определении полного перемещения w необходимо учесть составляющую перемещения, соответствующую первой гармонике:


Остальные компоненты перемещений и усилий могут быть найдены из соотношений (8.1)—(8.3).

Приближенная теория цилиндрической оболочки построена в работе [8]. Она позволяет получить замкнутые решения широкого круга задач и провести оценку перемещений и усилий в оболочках при самых разных видах несимметричной нагрузки.

9. Разностные схемы решения задач

Расчет конструкций, имеющих сложную конфигурацию и граничные условия, проводится дискретными методами. Одним из наиболее эффективных дискретных методов является метод конечных разностей (МКР). Он был использован применительно к расчету мягких оболочек в работе [7].

Система дифференциальных уравнений мягкой оболочки в перемещениях имеет следующий вид:


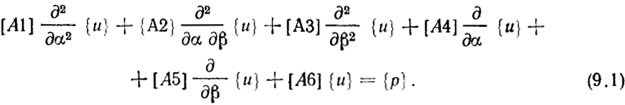
Матрицы [A1]...[A6] имеют размер 3X3. Компоненты этих матриц получаются из соотношений (3.22)—(3.24). В правой части — вектор полной поверхности нагрузки.

Уравнение (9.1) в частных производных имеет второй порядок по каждой координате. Разностная форма записи первой и второй производных по β с точностью 0(h⁴) имеет вид


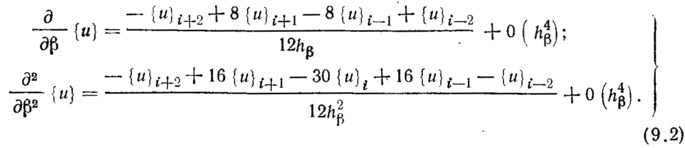
Область интегрирования, границы которой совпадают с линиями кривизны, разбивается на N участков в направлении β и М участков в направлении α. Искомой оказывается система полных векторов функций {u}, взятых в М точках направления α. Решение отыскивается по слоям в направлении α, при этом каждый слой есть дискретный разностный аналог исходной записи производных в направлении β (α=const). В приложении приведены таблицы, которые позволяют просто перейти от дифференциального уравнения к его конечно-разностному аналогу. В результате получается следующая система обыкновенных дифференциальных уравнений:


Компоненты матрицы [B1], [В2], [B3] вычисляются по формулам, приведенным в приложении. Размер матриц определяется числом участков в направлении β. Индекс j соответствует номеру точки на слое α=const (j=0,1,2,...).

Структура матриц [B2] и [B3] зависит от принятой разностной аппроксимации производных на слое. Для пятиточечной аппроксимации (9.2) это блочные пятидиагональные матрицы, каждый блок которых имеет размер 3X3. Матрица [B1] имеет блочную диагональную структуру, которая не зависит от аппроксимации производных на слое. Регулярность структуры матриц [B1], [B2], [B3] нарушается вблизи границы области, где необходимо ввести граничные условия. Для слоя α=const граничные условия имеют вид (3.21).



Чтобы не выходить за пределы области интегрирования, можно записывать первую производную в левых для правого края и в правых для левого разностях через шесть слоев, сохраняя точность аппроксимации 0(h⁴). Уравнения равновесия во втором и предпоследнем слоях необходимо записывать в конечных разностях со сдвигом на один слой влево и вправо для того, чтобы не выйти за пределы области интегрирования.

10. Применение метода матричной прогонки

Решение системы дифференциальных уравнений (9.3) будет проводиться численно в конечных разностях методом факторизации разностного матричного уравнения. Система уравнений (9.3) в центральных разностях может быть представлена в виде


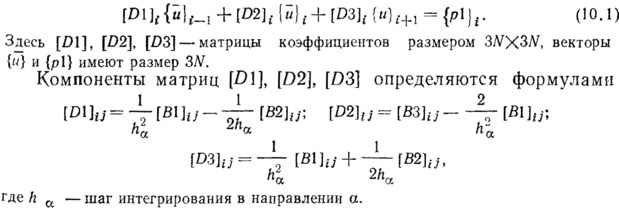
Решение трехточечного матричного уравнения (10.1) принимается в виде


Расчет по методу прогонки ведется в два этапа. Первый соответствует определению прогоночных матриц [Е] и вектора {L} при прямом ходе (движение от левой границы интегрирования вправо). Второй этап — обратный ход, при котором определяются полные векторы искомых функций {u} на каждом слое по формуле (10.2).

Решение проводится с учетом условий на каждой границе. В общем случае возможны кинематические, силовые или смешанные граничные условия. Представив их через перемещения и производные, можно эти условия записать следующим образом:


В конце интервала на правом крае i=M уравнение (10.5) имеет вид


Существенным недостатком данного решения является то, что при расчете необходимо помнить прогоночные матрицы и векторы для каждого слоя, а это требует большого числа обращений к внешним запоминающим устройствам ЭВМ. Избежать этого можно, используя процедуру встречной прогонки, которая позволяет получить решение линеаризованной системы уравнений значительно проще. Суть метода встречной прогонки состоит в том, что прогоночные матрицы и векторы определяются при движении в одном направлении, но запоминаются они лишь в тех сечениях, где необходимо иметь векторы искомых функций, которые определяются при движении в обратном направлении. Так же, как и в случае простой прогонки, решение ищется в виде


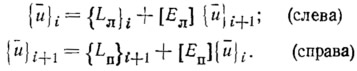
Расчет при движении в одном, а затем в другом направлении начинается с определения прогоночных матриц и векторов из граничных условий на каждом крае. Совместное решение последних двух уравнений позволяет определить искомый вектор {и} в каждом сечении.

11. Расчет оболочки пневматического свода

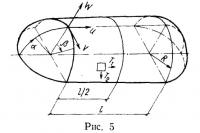
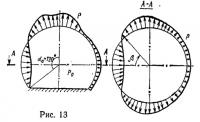
С помощью метода конечных разностей проведен расчет полуцилиндрической оболочки с торцами в виде четвертей сферы (рис. 5). Оболочка закреплена по опорному контуру и нагружена внутренним давлением p₀ и распределенной дополнительной составляющей внешнего усилия. Закон распределенного усилия принимался в виде р=—0,5p₀cosβ. В связи с тем, что и нагрузка, и рассматриваемая конструкция симметричны, расчет проводился для части оболочки, ограниченной плоскостями симметрии. Геометрические и физические параметры оболочки следующие: R=10 м; l=20 м; р₀=500 Па; Eh=2000 Н/м. При дискретизации на поверхности оболочки наносилась сетка, состоящая в окружном направлении из 15 участков, в меридиональном — из 41 участка для сферической оболочки и 26 для цилиндрической.

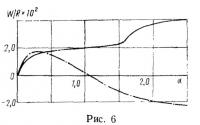
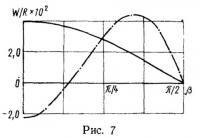
На рис. 6 и 7 приведены графики перемещений оболочки в двух плоскостях симметрии — меридиональной и для поперечного сечения оболочки (сплошная линия — перемещения от внутреннего давления, штрихпунктирная — от распределенной поверхностной нагрузки).

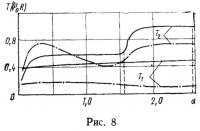
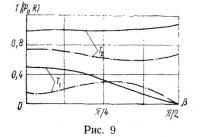
На рис. 8 и 9 представлены графики усилий Т₁ и Т₂. Ясно видна переходная зона вблизи стыка цилиндрической и сферической оболочек. Вдали от этой зоны усилия, как видно из графиков, описываются плавно меняющимися функциями.

Рис. 7. >

Рис. 8. >

Рис. 9. >

12. Метод конечных элементов

С помощью метода конечных элементов (МКЭ) могут быть решены самые разные задачи статики и динамики мягких оболочек. Он оказывается одним из наиболее удобных методов расчета сложных конструкций. Достоинства метода заключаются в его универсальности, возможности использования элементов различных типов, произвольности рассматриваемой области, простоте приемов построения элементов высокой точности. Один из важных этапов расчета конструкций по МКЭ —- построение матрицы жесткости элементов. Рассмотрим общую процедуру получения матрицы жесткости для элемента мягкой оболочки.

Воспользуемся условиями равновесия технической теории мягких оболочек в форме принципа возможных перемещений. Основному состоянию соответствует уравнение (3.9), которое в матричной форме имеет вид


От размера этого вектора зависит точность конечного элемента, а также возможность более правильного удовлетворения граничным условиям. Отметим, что узловыми перемещениями могут быть как сами перемещения, так и углы поворота. Это не является противоречием для мягкой оболочки. Условным углам поворота в энергетических соотношениях соответствуют фиктивные узловые изгибающие моменты, которые просто выражаются через поверхностные составляющие нагрузок. Введение в вектор; узловых перемещений углов поворота позволяет расширить возможности метода конечных элементов.

Подставим соотношение (12.4) в уравнение (12.3). Введя обозначения


из уравнения (12.3) получим соотношение для матрицы жесткости конечного элемента мягкой оболочки:


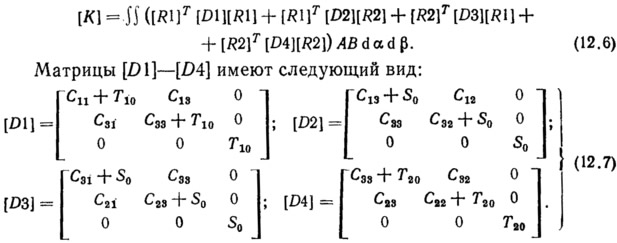
В этих матрицах коэффициенты жесткости, как правило, значительно больше величин усилий основного состояния. Поэтому в тех элементах матрицы, где коэффициенты суммируются с основными усилиями, последние могут не учитываться.

Из соотношений (12.3) и (12.4) можно получить также вектор узловых усилий


Окончательное уравнение, связывающее узловые усилия и узловые перемещения конечного элемента мягкой оболочки, может быть представлено в виде


В уравнениях (12.6) и (12.8) интегрирование ведется по недефор-мированной поверхности элемента. Элементы могут иметь самую разную геометрию. Матрица [К] квадратная: число составляющих в строке, так же как и в столбце, соответствует числу степеней свободы элемента.

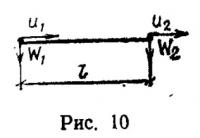
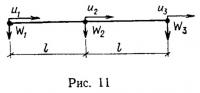
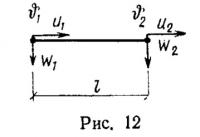
На рис. 10—12 представлены три вида одномерного конечного элемента; первый имеет две узловые точки и по два узловых перемещения в каждой точке, второй — промежуточную узловую точку посередине элемента; всего в элементе шесть степеней свободы, в каждой из двух узловых точек третьего элемента — три степени свободы. Построим матрицы жесткости и векторы узловых сил для каждого злемента.

Рис. 10. >

Рис. 11. >

Рис. 12. >

Положим, что поле перемещения для случая, указанного на рис. 10, аппроксимируется следующим образом:


Введя вектор узловых перемещений в соответствии с рис. 10


определим составляющие α₀...β₁ матрицы (12.10). Они выражаются через узловые перемещения. Тогда вектор {и} можно представить в виде {u}=[Ф]{u_n}, где матрица [Ф] равна


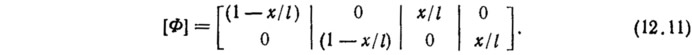
С помощью соотношения (12.5) определим составляющие матрицы, а из (12.6) — матрицу жесткости элемента:


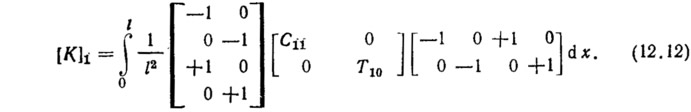
В последней зависимости из (12.6) оставлено только первое слагаемое, так как остальные члены соответствуют двумерной задаче. В матрице [D1] отсутствует вторая строка и второй столбец, а также принято, что T₁₀<<C₁₁. Окончательное соотношение для матрицы жесткости элемента (12.10) получается после перемножения матриц в выражении (12.12):


Коэффициенты матрицы выражаются через узловые перемещения u₁, w₁, u₂, w₂, u₃, w₃ и позволяют определить матрицу [Ф]:


В этом элементе более точно аппроксимируются перемещения. Поле перемещений соответствует уже не ломаным линейным зависимостям, а параболическим кривым.

Элемент третьего вида (см. рис. 12) имеет две узловые точки, в каждой из которых задаются не только перемещения u и w, но и угол поворота v. Таким образом, вектор узловых перемещений имеет вид {u_n}={u₁w₁v₁u₂w₂v₂}^T.

Поле перемещений принимается в форме


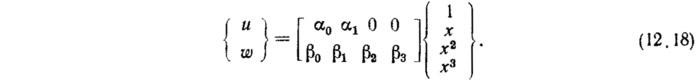
Матрица, связывающая перемещения с узловыми перемещениями, имеет следующий вид:


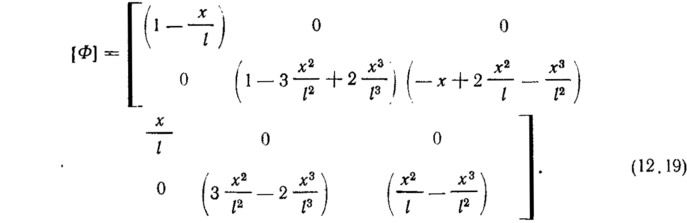
Здесь учитывается связь между перемещением w и углом поворота v:


Подстановка зависимости (12.19) в уравнения (12.6) и (12.8) позволяет определить матрицу жесткости элемента


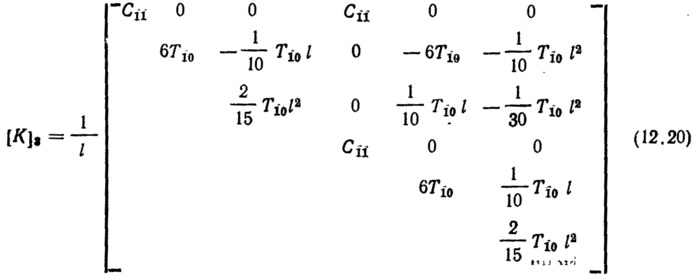
и вектор узловых сил при равномерно распределенной нагрузке


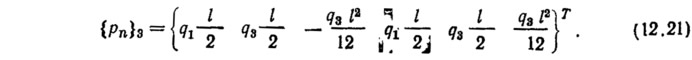
С помощью этого элемента (см. рис. 12) удается состыковать соседние элементы по углу поворота непосредственно в узловой точке, что является большим преимуществом, так как более удобно составляется глобальная матрица жесткости и удовлетворяются граничные условия.

Каждый из рассмотренных одномерных конечных элементов имеет свои особенности. Они отличаются точностью, размером матриц жесткости, требованиями, предъявляемыми к ним при составлении глобальной матрицы. Здесь приведены прежде всего методологические основы построения элементов. Для многих задач, в которых применяется теория мягких оболочек, необходимо использовать более сложные двумерные элементы. При этом возникают проблемы аппроксимации исходной поверхности, описания криволинейных элементов, нахождения интегралов при определении коэффициентов матрицы, решения сложной системы уравнений и многие другие. Но общая последовательность построения элементов, которая приведена выше, остается той же. Общее соотношение между узловыми перемещениями и узловыми силами имеет такой же вид, что и уравнение (12.9), но размер матрицы жесткости соответствует общему числу степеней свободы рассматриваемой оболочки. Введение в полученную систему уравнений граничных условий, записанных относительно перемещений и их производных, и решение полученных уравнений позволяет определить неизвестные узловые перемещения. По соотношениям (12.4), (1.4), (3.18) находят поле перемещений, деформаций и усилий в оболочке.

13. Расчет сферической оболочки при несимметричной нагрузке методом конечных элементов

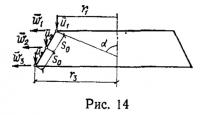
Приведем решение задачи определения деформированного состояния сферической оболочки, нагруженной внутренним давлением и ветровой нагрузкой [9] (рис. 13). Суммарное давление в каждой точке поверхности таково, что зон складок в оболочке не возникает. В качестве конечного элемента принят усеченный конус (рис. 14) с девятью степенями свободы. Наиболее удобно в этой задаче применять перемещения u, v, w, которые связаны с перемещениями u, v, w соотношением


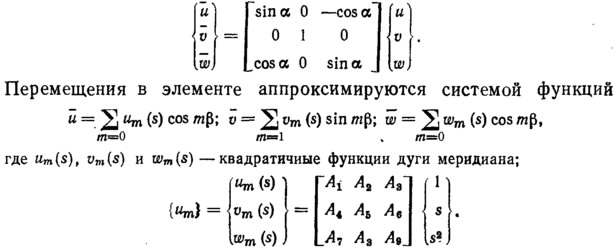
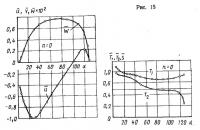
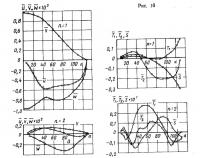
Составляющие матрицы А₁—А₉ выражаются через узловые перемещения, что позволяет построить матрицу [Ф]. Из соотношения (12.5) определяются матрицы |R1], [R2] — основные элементы матрицы жесткости (12.6). На рис. 15 и 16 по результатам работы [10] представлены графики расчета оболочки при 43 конечных элементах и значениях констант


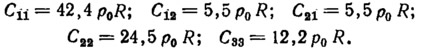
Приведены кривые перемещений и усилий в оболочке при m=0 (осесимметричныйслучай), m=1 и m=2. Расчеты показывают, что при больших т величины перемещений и усилий незначительны и их можно не принимать во внимание.

Рис. 14. >

Рис. 15. >

Рис. 16. >

14. Заключение

Техническая теория мягких оболочек имеет большие возможности получения практически важных и одновременно достаточно достоверных результатов определения напряженного деформированного состояния самых различных конструкций. Введение некоторых дополнительных упрощений позволяет построить приближенные аналитические решения сложных задач. Они бывают необходимы для оценки величин усилий и перемещений и являются основой для дальнейших уточнений. Общая теория использована при создании систем алгоритмов и программ расчета, основанных на применении ЭВМ и современных дискретных методов.

Приложение

Матрицы уравнений равновесия технической теории мягких оболочек:


Матрицы граничных условий:


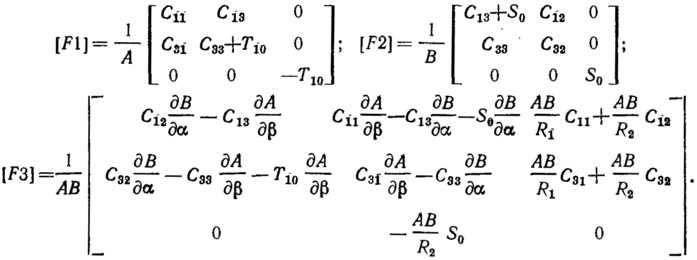
Матрицы уравнений равновесия оболочки вращения (основное состояние осесимметрично):


Матрицы геометрических соотношений оболочки вращения:


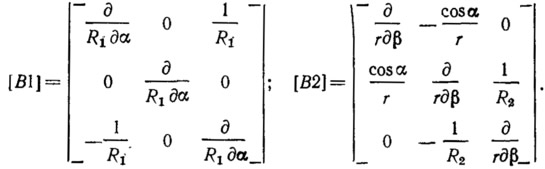
Матрицы уравнений равновесия оболочки вращения для каждой гармоники т (применение метода разделения переменных):


Матрицы геометрических соотношений для каждой гармоники:


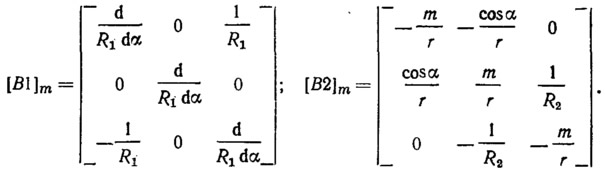
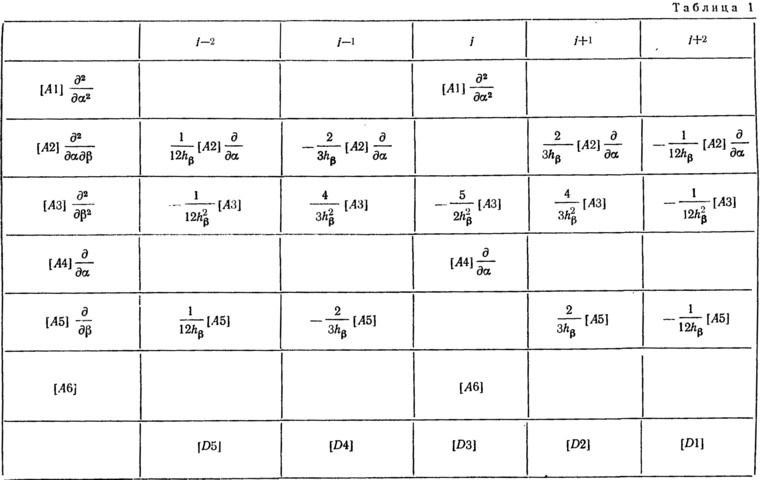
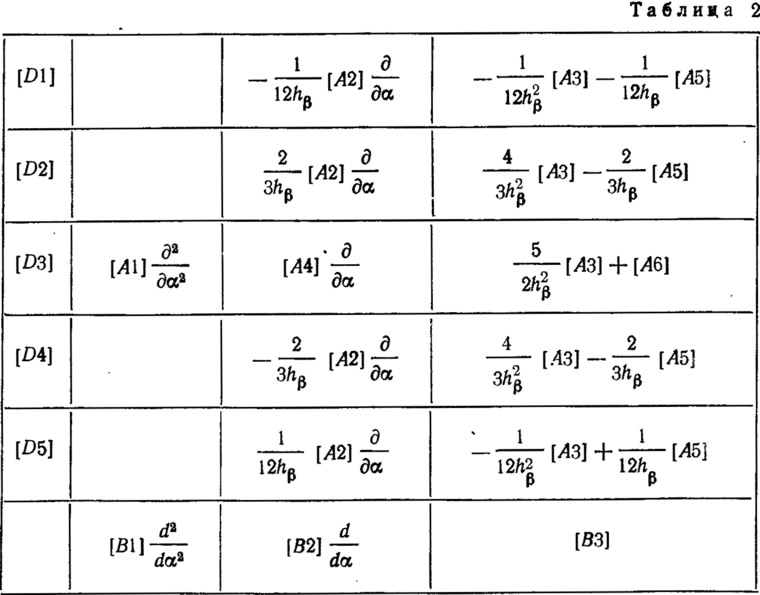
Преобразование дифференциального уравнения в конечно-разностное [точность 0(h⁴)] дано в табл. 1 и 2.

Компоненты матриц [В1], [В2], [B3] дифференциального уравнения (9.3):

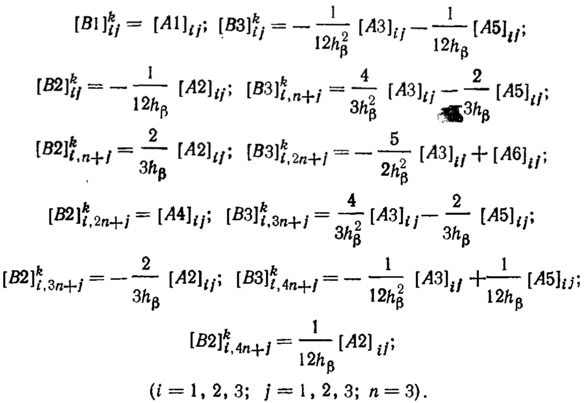
Список литературы

• 1. Алексеев С. А. Основы общей теории мягких оболочек.— В сб.: Расчет пространственных конструкций. Вып. XI, М., 1967.
• 2. Григорьев А. С. Равновесие безмоментной оболочки вращения при больших деформациях — Прикладная математика и механика, 1961, т. 25, вып. 6.
• 3. Грин А., Адкиис Дж. Большие упругие деформации и нелинейная механика сплошной среды. М., Мир, 1965.
• 4. Усюкии В. И. Об уравнениях теории больших деформаций мягких оболочек.— Известия АН СССР, МТТ, 1976, № 1.
• 5. Балабух Л. И., Усюкии В. И. Приближенная теория мягких оболочек вращения.— Труды VIII Всесоюзной конференции по теории оболочек и пластин. Ростов-на-Дону, 1971.
• 6. Усюкии В. И. Деформации мембранных оболочек вращения.— Известия АН СССР. Механика и машиностроение, № 2, 1964.
• 7. Усюкин В. И., Терещенко В. А., Борсов Р. Г. Разностные методы решения двумерных задач статики мягких оболочек.— В сб.: Расчет пространственных конструкций. Вып. XVIII, М., 1979.
• 8. Усюкин В. И. Деформация мембранной торообразной оболочки.— Труды VII Всесоюзной конференции по теории пластин и оболочек. Днепропетровск, 1969.
• 9. Сдобников А. Н. Применение метода конечных элементов к расчету мягких оболочек вращения.— Сообщения Дальневосточного высшего инженерноморского училища. Вып. 34. Владивосток, 1976.
• 10. Усюкин В. И., Терещенко В. А., Сдобников А. Н., Панов С. В. Расчет пневматических строительных конструкций с использованием ЭВМ. Доклады Международной конференции по облегченным пространственным конструкциям ИАСС. М., Стройиздат, 1977.