Основной параметр, необходимый для расчетов,— пропускная способность канализационного стояка, т. е. максимально допустимый расход сточной жидкости, не вызывающий срыва гидравлического затвора, либо критический расход жидкости, соответствующий моменту срыва гидравлического затвора.
Анализ и результаты экспериментальных исследований показывают, что опускное движение водовоздушной смеси в канализационном стояке происходит под действием массы жидкости и обусловливает возникновение разрежений. При гидравлическом моделировании необходимо знать, какая из этих двух сил — масса воды или разрежения — преобладает и оказывает определяющее влияние на процесс движения.
Как известно, первым необходимым условием при гидравлическом моделировании является геометрическое подобие двух систем — модели и натуры, т. е. подобие их конструкций и характерных линейных размеров.
За масштаб моделирования обычно выбирают отношение диаметров натуры и модели:
Тогда отношение площадей их живых сечений:
Этих двух условий недостаточно для моделирования процессов в канализационных стояках. Поскольку установлено, что пропускная способность стояков существенно зависит от условий входа в них жидкости и в определенных пределах от высоты стояков, геометрически подобными системами являются такие, у которых, помимо условий (39) и (40), соблюдаются также следующие: (Dст/dотв)п=(Dст/dотв)м, (αн=αм и Lн/Dн=Lм/Dм.
При движении водовоздушной смеси в канализационном стояке вода занимает часть сечения стояка:
где k<1, ωст — площадь сечения стояка.
При этом площадь, нанимаемая воздухом:
площадь, занимаемая смесью вода + воздух, равна площади сечения стояка:
Из условий неразрывности потока следует:
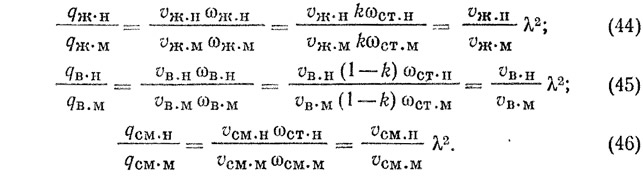
Уравнения (44)—(46) показывают, что моделирование расходов жидкости, воздуха и смеси (вода + воздух) подчиняется одному закону. Для моделирования этих параметров необходимо отношение скоростей жидкости, воздуха и смеси натуры и модели выразить через масштаб моделирования λ.
Из гидравлики известно, что если движение жидкости происходит под действием ее массы, то отношение инерционных сил к силам тяжести выражается через критерий Фруда:
Из (47) следует:
или
С учетом (49) можно установить, что
Если же при движении водовоздушной смеси в канализационном стояке преобладающими являются силы давления, то моделирование осуществляют по «числу Эйлера»:
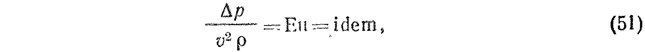
где ρ — плотность воды (воздуха, смеси); Δр — разрежение в стояке.
Из (51) следует:
При моделировании процессов движения жидкостей с одинаковой плотностью в случае равенства разрежений:
Тогда уравнения (44) — (46) принимают вид:
Справедливость первого отношения в уравнении (54) легко проверить по экспериментальным данным, представленным в табл. 4 и табл. 5. Из (54) следует:
Экспериментальные данные А. И. Карпинской, швейцарских и французских исследователей хорошо подтверждают результаты расчета по формуле (55).
Например, по А. И. Карпинской (для стояков диаметрами 100 и 125 мм):
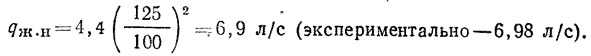
По К. Bosch (для стояков диаметрами 100 и 150 мм):
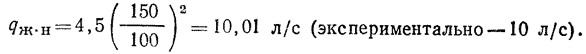
По H. Schellenberg (для стояков диаметрами 50 и 100 мм):

Таким образом, преобладающей силой при безнапорном течении водовоздушной смеси в канализационных стояках является разрежение, а не масса жидкости, и моделировать процессы следует по числу Эйлера. Формула (51) дает возможность рассчитать среднюю скорость движения жидкости в стояках различных диаметров, что, безусловно, проще, чем ее экспериментальное определение.
При определении средней скорости воспользуемся следующими зависимостями для среднего динамического давления при движении двухфазной смеси по вертикальным трубопроводам:
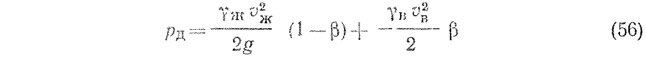
и
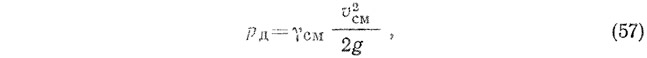
где γж, γв и γсм — объемная масса соответственно жидкости, воздуха и смеси;
здесь β — объемное расходное газосодержание, определяемое по формуле
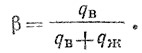
Совместное решение уравнений (56) и (57) дает возможность определить среднюю скорость жидкости, м/с:
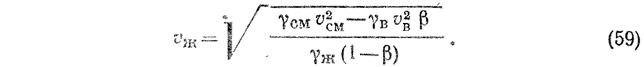
При этом скорость воздуха определяется по формуле (31), его расход — по формуле (32), а скорость смеси — как частное от деления расхода смеси на площадь живого сечения канализационного стояка.
Для расчета числа Эйлера требуется определить плотность водовоздушной смеси:
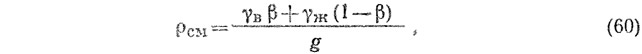
где g — ускорение свободного падения, м/с2.
Результаты расчетов скоростей жидкости, воздуха и смеси, а также числа Эйлера представлены в табл. 11. Расчеты выполнены по эмпирическим формулам (31) и (35), а также по формулам (51), (59) и (60) для геометрически подобных систем канализации различных конструкций при разрежениях 20, 40 и 65 мм вод. ст.
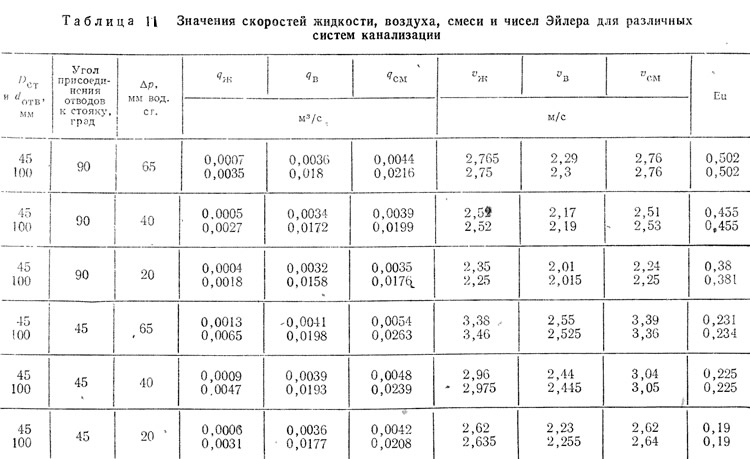
Приведенные данные подтверждают, что в геометрически подобных системах канализации равные разрежения возникают при одинаковых скоростях движения жидкости, воздуха и смеси и равных значениях чисел Эйлера. Значения скоростей воздуха соответствуют течению воздуха в вытяжной части стояка, т. е. выше места входа жидкости в стояк.
Имея данные по расходу воздуха qв, фактически поступающего в стояк, можно рассчитать скорость воздуха, движущегося в стояке ниже его сжатого сечения, т. е. при наличии жидкостной пленки, омывающей внутреннюю поверхность стояка. Для этого необходимо определить площадь живого сечения воздуха, движущегося на участке стояка ниже места входа в него жидкости.
Рассчитаем площадь живого сечения жидкостной пленки для случая, когда разрежение равно 65 мм вод. ст.
Площадь живого сечения воздушного потока определится как разность между площадями живых сечений стояка и жидкостной пленки:
Скорость воздуха, движущегося вместе с жидкостью на участке стояка, расположенном ниже места входа в него жидкости:
т. е. равна скорости течения жидкости и смеси.
Аналогичные расчеты также показывают, что средняя скорость движения воздуха равняется средней скорости течения жидкости и смеси и для других разрежений.
На основании расчетов можно установить, что при критическом разрежении расход жидкости занимает лишь 16,4% живого сечения стояка (при α=45° — примерно 25%).
Все приведенные рассуждения относятся к системам канализации, в конструкцию которых входит один (сточный) стояк. Однако, как было показано выше, при устройстве дополнительной вентиляции в зданиях ограниченной высоты течение жидкости и воздуха в канализационном стояке может практически не сопровождаться возникновением разрежений. В этом случае остается лишь одна сила, под действием которой движется жидкость — масса самой жидкости. Расходы жидкости, воздуха и смеси при этом должны моделироваться по уравнению (50).
Рассмотрим для примера две системы канализации с вентиляционными стояками, обеспечивающими течение жидкости и воздуха без разрежений. Характеристика первой системы, которую мы принимаем за модель: Dст=dотв=50 мм, L>90Dст, α=90°; характеристика второй системы («натура»): Dст=dотв=100 мм, L>90Dст, α=90°.
Допустим, что в первой системе расход сточной жидкости составляет 1 л/с. Следовательно, для обеспечения условия подобия расход жидкости во второй системе должен вставлять:

При движении жидкости и воздуха в канализационном стояке не возникает разрежение, если количество . воздуха, поступающего в стояк, равняется эжектирующей способности жидкости. Таким образом, расход воздуха, поступающего в первую систему: Qв=7,31 л/с; во вторую систему: Qв=43,6 л/с.
По теории подобия
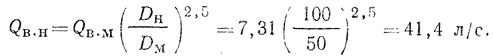
Относительная ошибка при расчетах по формуле (30) и по теории гидравлического подобия в данном случае ~5%.
Расход смеси вода + воздух в первой системе равен:
во-второй системе
По теории подобия

Относительная ошибка в данном случае составляет ~4,5%.
Таким образом, при течении жидкостей с одинаковой плотностью в канализационных стояках без возникновения разрежений расходы жидкости, воздуха и смеси (вода + воздух) моделируются по уравнению (50); в случае возникновения разрежений одинаковой величины — по уравнению (54).
Необходимо отметить, что все приведенные здесь рассуждения справедливы для канализационных стояков, имеющих вытяжную часть. Для невентилируемых стояков моделирование процессов подлежит дальнейшему анализу в связи с тем, что расход воздуха, увлекаемого в стояк жидкостью, неизвестен. Расчет величины разрежений в таких стояках по эжектирующей способности жидкости условен.
Процессы движения водовоздушной смеси в невентилируемом стояке отличны от процессов в стояках с вытяжной частью. В частности, можно предположить, что при движении жидкости в невентилируемый стояк воздух может поступать снизу вверх, т. е. против движения воды. В этом случае возникают дополнительные сопротивления движению жидкости и трудно определить, какие силы преобладают. Возможно, что при моделировании процессов в невентилируемом стояке следует одновременно учитывать не один, а несколько критериев гидравлического подобия, поэтому решение задачи резко усложняется.
По результатам экспериментальных исследований, представленным в табл. 10, можно сделать вывод, что расходы жидкости в невентилируемых геометрически подобных стояках моделируются как отношение диаметров этих стояков:
Кроме, того, отношение скоростей смеси вода + воздух в натуре и на модели равно 1 при Δр=const:
что следует из уравнения (37).
