Таблицы размеров прокатных профилей

Номограммы служат для приближенного определения размеров балок из прокатных двутавровых профилей. Номограммы 1 содержат данные для профилей высотой до 400 мм, а 2 — для более высоких.

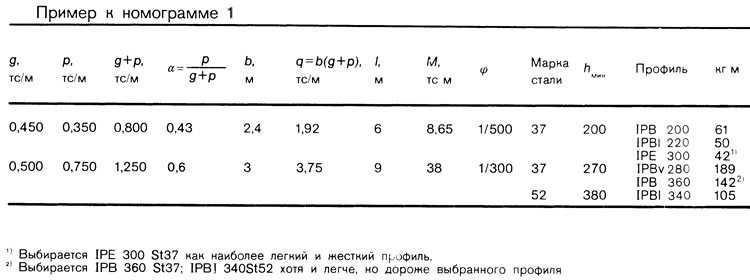
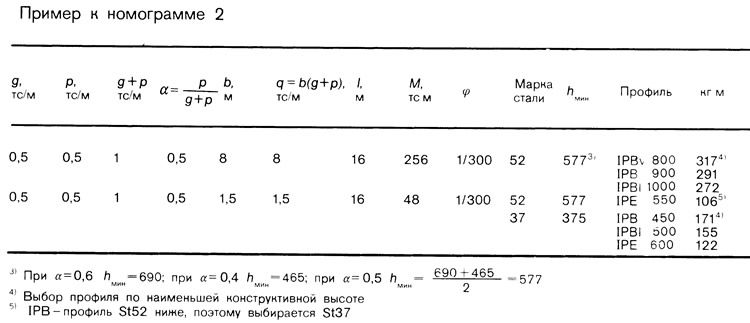
Нагрузка

Равномерно распределенная нагрузка на балку q тс/м² определяется по формуле


где g — постоянная нагрузка, тс/м²;
р — временная нагрузка, тс/м²;
b — ширина грузовой площади, м.

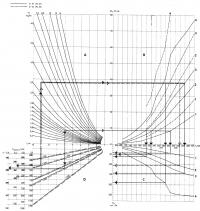
Номограмма А - определение изгибающих моментов.

Изгибающий момент (тс.м) от равномерно распределенной нагрузки q в однопролетной балке пролетом l:


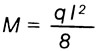
По номограмме А, двигаясь от размера пролета l вверх до пересечения с соответствующей кривой нагрузки q и затем вправо, на вертикальной оси находят значение момента М.

Номограмма 8 - определение профиля балки.

Номограмма В дает возможность определить размеры четырех типов профилей из двух марок стали при допускаемых напряжениях:



Для этого нужно от значения момента М, двигаясь вправо до пересечения с кривой профиля и затем вниз, на горизонтальной оси найти требуемый профиль; если точка лежит между двумя размерами профилей, то выбирается более высокий (правее).

Найденный по номограмме В профиль не может выть принят до установления достаточности его высоты по условию допускаемого прогиба.

Номограмма С - определение массы балки.

Масса профиля определяется на вертикальной оси номограммы С.

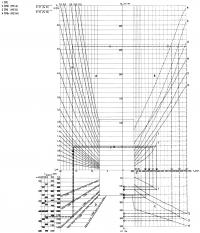
Номограмма D - определение минимальной высоты балки по заданному относительному прогибу.

Прогиб f однопролетной балки симметричного сечения пролетом l, нагруженной равномерно распределенной нагрузкой, зависит от высоты балки h, значений краевых напряжений и модуля упругости материала Е, значение которого для всех строительных сталей одинаково (Е = 2100 тс/см²).

Относительный прогиб для этого случая определяется по формуле:


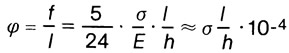
Требуемая высота балки при полном использовании допускаемого напряжения составляет:


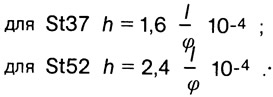
Номограмма D построена для относительных прогибов αδ=f/l=1/200, 1/300, 1/500 при двух марках сталей.


В большинстве случаев прогиб определяется только от временной нагрузки р. Доля временной нагрузки р от суммарной нагрузки g + р:


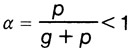
Временная нагрузка, составляющая часть всей нагрузки, вызывает напряжения αδ и прогиб αf . Прогиб от постоянной нагрузки может компенсироваться строительным подъемом. Так как размер прогиба находится в прямой зависимости от нагрузки и высоты балки, то минимальная высота балки h_мин=αh; где h — требуемая высота балки, определяемая по номограмме D при полном использовании допускаемого напряжения материала. Для удобства слева от шкалы высот балки при α=1 нанесены еще три шкалы, которые позволяют определять h мин для значений α=0,4; 0,6 и 0,8.

Наименьшую допустимую высоту балки определяют по номограмме D следующим образом. От размера пролета балки l (на оси абсцисс) двигаются вниз до пересечения с прямой, характеризующей заданные относительный прогиб и марку стали, и далее влево до шкалы соответствующего значения


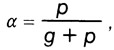
по которой определяют h_мин.

Высота балки, определенная по номограмме несущей способности В, должна быть не менее h_мин , полученной из номограммы прогибов D.