Расчет конструкции каркаса зданий повышенной этажности

Современные конструкции каркаса зданий повышенной этажности выполняются, как уже было сказано в главах 9 и 10, в основном по связевой схеме. В связевой схеме каркаса все горизонтальные нагрузки полностью воспринимаются вертикальными и горизонтальными диафрагмами жесткости, рамы каркаса работают только на вертикальные нагрузки.

Рассмотрим методику расчета каркаса связевой схемы.

В практике проектирования многоэтажных зданий используются, как правило, приближенные методы расчета. Такой подход представляется вполне оправданным, поскольку сами предпосылки, положенные в основу расчета, весьма условны. Как известно, любая идеализированная схема здания никогда не бывает тождественна действительной работе конструкций. Кроме того, в расчете каркаса, выполняемого из железобетона, .фигурируют жесткостные характеристики конструктивных элементов и их соединений, которые являются весьма приближенными. Их значения существенно меняются при трещинообразовании и вследствие ползучести бетона. Во всех статических расчетах используются методы, построенные на принципе независимости действия сил, однако железобетон не подчиняется этому принципу. Приведенные предпосылки расчета делают невозможным получение точных результатов при расчете сложных систем и определяют целесообразность использования приближенных способов, которые дают возможность получить порядок усилий, необходимых для проектирования Конструкций.

1. Определение расчетных нагрузок

Методика определения вертикальных нагрузок — постоянных и временных, горизонтальных — ветровых нагрузок, а также расчетных сочетаний воздействий была приведена в главе 8 и может быть полностью использована для расчета каркасных зданий.

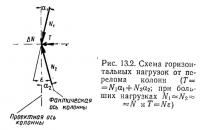
Рассмотрим здесь возможные упрощения при определении ветровой нагрузки путем введения некоторых допущений. В главе 8 уже были сделаны допущения о том, что при определении периода собственных колебаний принимается только первая форма колебаний, т. е. по основному тону, а также об использовании трапециевидной эпюры статического скоростного напора ветра. Если к тому же предположить, что первая форма колебаний выражается прямой линией¹, то воздействие пульсации ветрового напора можно представить в виде треугольной нагрузки (рис. 13.1) с ординатой на уровне верха здания:



где q₁ и q_H — статический скоростной напор ветра на уровне низа и на высоте H; ξ — динамический коэффициент, определяемый в зависимости от периода первой формы собственных колебаний здания по графику на рис. 2 СНиП II-A. 11-62; m — коэффициент пульсации ветрового напора, равный 0,2.

Учитывая условность определения периода собственных колебаний расчетным путем, для чего необходимо знать действительную жесткость здания и жесткость основания (эти величины и являются в значительной мере условными), целесообразно принимать в расчетах на прочность каркаса зданий большой высоты — более 20 этажей — максимальное значение динамического коэффициента ξ для железобетона, равное 2,4.

При этом верхняя ордината нагрузки от пульсации ветра по формуле (13.1) будет равна:


Поясним допустимость такого подхода к определению расчетных ветровых нагрузок. Характерной особенностью жилых и общественных зданий является относительно равномерное расположение масс по высоте сооружения, т. е. М₁=М₂=...=М, а также грузовых поэтажных площадей для определения ветровых нагрузок S₁, S₂=...S.

С учетом этих допущений формула для определения формы колебаний запишется в виде:


При этом динамическая часть ветровой нагрузки будет равна:



а динамическая нагрузка на 1 м² фасада


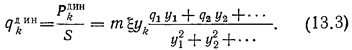
Таким образом, удалось исключить массы отдельных зон.

Последнюю формулу запишем в виде:

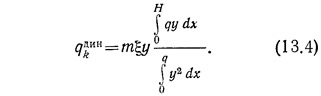
Для интегрирования последнего выражения необходимо представить нагрузку q как функцию высоты x. С достаточной точностью можно принять следующее выражение для статической нагрузки:


Подставляя выражение (13.5) в формулу (13.4), получим:



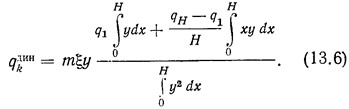
Дальнейшие вычисления связаны с определением формы колебаний здания у. Если форма колебаний здания близка к прямой линии


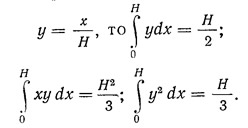
Потому из выражения (13.6) получаем:


Отсюда максимальная ордината треугольной эпюры ветровой нагрузки равна выражению (13.1).

Изгибающий момент в основании от треугольной эпюры (случай 1)


Ввиду того что форма колебаний принята по прямой линии, а не по квадратной параболе, определим величину погрешности. Если форма колебаний здания представляет квадратную параболу у=х²/Н², то



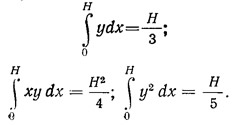
Подставляя эти выражения в формулу (13.6), получаем:


Таким образом, динамическая «добавка» представляет собой квадратную параболу с максимальной ординатой:


Изгибающий момент в основании от этой нагрузки (на 1 пог. м ширины здания)


Отношение изгибающих моментов от параболической и треугольной эпюры


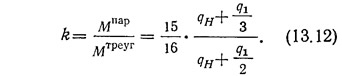
Например, для здания высотой 70 м отношение q_H/q₁=2, тогда



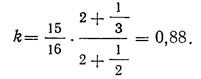
Отсюда видно, что величина максимального момента мало зависит от формы колебаний здания.

Приведем формулы для определения полных изгибающих моментов на уровне земли от динамической и статической части ветровой нагрузки в случае, когда эпюра статической части ветровой нагрузки представлена в виде трапеции (см. рис. 13.1,а):


Полагая ξ=0, получим изгибающий момент на уровне земли от статической части ветровой нагрузки:


Максимальный прогиб вертикальных диафрагм постоянного сечения от треугольной нагрузки (см. рис. 13.1, б)


Для облегчения вычислений в табл. 13.1 приведены величины изгибающих моментов на уровне земли (на 1 пог. м ширины здания) от нормированной (по СНиП) эпюры ветровой нагрузки для Москвы, нижняя ордината статической нагрузки, вычисленная из условия равенства моментов от трапециевидной и от нормированной эпюры статической нагрузки и верхняя нормированная ордината статической ветровой нагрузки².


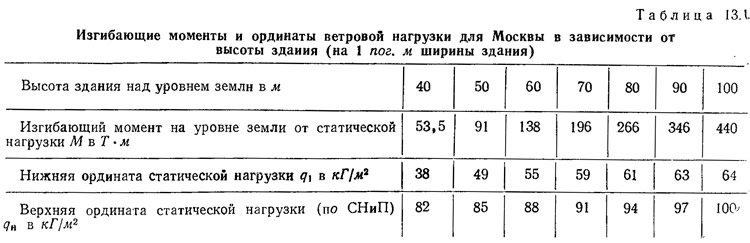
Величина q₁, взятая из этой таблицы, должна подставляться в формулу (13.7).

Предлагаемая упрощенная методика определения расчетной ветровой нагрузки по сравнению с методикой «Временных указаний по проектированию крупнопанельных жилых домов высотой 10—16 этажей» (см. главу 8), основанной на определении динамического воздействия ветра в зависимости от получаемого расчетным путем периода собственных колебаний, приводит к погрешности в определении усилий — изгибающих моментов и поперечных сил для зданий высотой в пределах 25 этажей — примерно на 8—12%, что вполне приемлемо.

Другим горизонтальным воздействием на каркас являются случайные нагрузки, возникающие вследствие перелома осей колонн по высоте здания. Определение величины этой нагрузки связано с исследованием общей устойчивости каркаса здания, работающего как внецентренно сжатая консоль под воздействием вертикальных и горизонтальных нагрузок.

Особенность каркаса связевой системы состоит в том, что вертикальные нагрузки, стремящиеся вывести его из состояния устойчивого равновесия, воспринимаются большим числом колонн, собственная жесткость которых мала. Таким образом, здание удерживается в состоянии устойчивого равновесия только связевыми диафрагмами жесткости.

Влияние деформации внецентренно сжатого железобетонного стержня на величину усилий, в соответствии с §7.51 СНиП II-B.1-62, учитывается умножением эксцентрицитета на повышающий коэффициент η, равный:


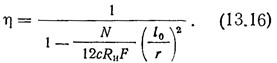
Особенности работы диафрагм жесткости, вынужденных удерживать в устойчивом состоянии все вертикальные несущие конструкции каркаса, могут быть учтены при определении свободной высоты диафрагм. Она определяется сопоставлением эйлеровых критических сил для собственно диафрагмы и для диафрагмы, удерживающей связанные с ней колонны³.

Для собственно диафрагмы

Для диафрагмы, удерживающей все здание,

Разделив выражение (13.18) на (13.17), получим:

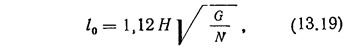
здесь Н — высота здания; G — суммарная вертикальная нагрузка на здание; N — часть суммарной вертикальной нагрузки, приходящаяся на связевые плоскости одного направления.

При регулярном плане здания отношение может приближенно приниматься равным отношению общего числа колонн к числу колонн, входящих в состав стен жесткости одного направления.

Подставив выражение (13.19) в (13.16) и учтя, что радиус инерции стен жесткости r=√J/F, получим:


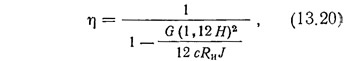
где — расчетное сопротивление бетона диафрагм сжатию при изгибе; с — по формуле (112) СНиП II-B. 1-62; J — сумма моментов инерции всех стен жесткости одного направления. Для обеспечения необходимой устойчивости здания величина η должна находиться в пределах 1—1,5.

Влияние длительного действия нагрузки учитывается заменой в формуле (13.20) веса здания приведенным весом, вычисляемым по формуле


Так как вертикальная нагрузка, действующая на связевые плоскости, может быть различной для диафрагм продольного и поперечного направления, то и свободная высота здания для продольного и поперечного направления оказывается разной.

Поэтому прочность внецентренно сжатых элементов обеспечивается в расчете умножением эксцентрицитета на повышающий коэффициент η, отдельно для продольного и поперечного направления. Увеличение эксцентрицитета эквивалентно увеличению усилий от горизонтальных нагрузок.

2. Определение усилий в дисках перекрытий

Перекрытия в каркасной системе здания кроме восприятия вертикальных нагрузок обеспечивают неизменяемость здания в плане и совместно с вертикальными диафрагмами жесткости — общую устойчивость сооружения, а также распределяют горизонтальные нагрузки на эти диафрагмы.

Основными нагрузками на диски перекрытий являются ветровая нагрузка и нагрузка, возникающая от переломов осей колонн, а также в отдельных случаях усилия, вызываемые колебаниями температуры, деформациями оснований фундаментов. Ветровая нагрузка определяется по грузовой площади, высота которой равна расстоянию между дисками и, как правило, равномерно распределена по длине диска.

Нагрузка на диски от переломов осей колонн возникает вследствие отклонений осей колонн от вертикали. В результате погрешностей монтажа линия действия нормальной силы в колонне оказывается ломаной, причем переломы ее располагаются в уровне перекрытий.

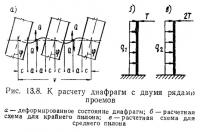
Переломы приводят к возникновению горизонтальной составляющей (рис. 13.2)


где N — нормальная сила в колонне; ε — расчетный угол перелома оси колонны.

В специальной литературе и действующих нормативных документах отсутствует методика определения нагрузок на перекрытия от переломов колонн. Это не .имело существенного значения в малоэтажных каркасных зданиях, так как нормальные силы в колоннах этих зданий невелики, вследствие чего горизонтальные нагрузки на перекрытия оказывались также незначительными. В высотных зданиях, возведенных за рубежом и построенных в 50-е годы в Москве, перекрытия выполнены в монолитном железобетоне и имеют достаточное количество конструктивной арматуры, способной свободно воспринимать горизонтальные нагрузки, возникающие от переломов колонн. Проблема стала острой сейчас, так как в новых типах многоэтажных зданий перекрытия выполняются из сборного железобетона и должны обладать необходимой прочностью для восприятия усилий, возникающих в горизонтальных дисках.

В верхней части многоэтажных зданий, при небольших нормальных силах в колоннах, основной нагрузкой на диски перекрытий является ветер. В нижней части этих зданий ветровая нагрузка уменьшается, а нормальные силы в колоннах растут и, таким образом, усилия от перелома колонн становятся для дисков перекрытий решающими.

Расчетный угол перелома колонн можно определить исходя из нормируемых допусков установки колонн. Так, по табл. 6 СНиП I-A.4-62 допуск невертикальности установки колонн длиной 6 м при монтаже по классу точности 2-У равен 30 мм. Если предположить, что стык двух смежных колонн сместился с проектного положения на половину допуска — на 15 мм, а противоположные концы этих колонн сместились на ту же величину,но в другую сторону, то угол перелома 6-метровых колонн будет:


Для проверки этой величины и выявления реальных углов перелома осей колонн были проанализированы результаты монтажа одного из первых высотных сооружений — здания института Гидропроект. Более тысячи замеренных в натуре углов перелома колонн подверглись статистической обработке. В результате обработки расчетный угол перелома одной колонны оказался равным: ε=0,012.

При учете одновременного воздействия на диски перекрытия n переломов колонн по анализу переломов в каркасе здания института Гидропроект расчетные углы переломов колонн можно принимать:


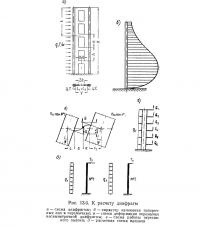
где n — количество воздействий переломов колонн на диск перекрытия, одновременно учитываемых в рассматриваемой расчетной схеме (рис. 13.3).

На рис. 13.3, б сплошной линией изображена кривая, характеризующая зависимость расчетных углов перелома ε_п от количества колонн, одновременно действующих на диск перекрытия. Точками показаны переломы, полученные на монтаже здания института Гидропроект.

Строительные нормы, действующие в ГДР, рекомендуют при расчете дисков перекрытий принимать на них от колонн горизонтальную силу, равную 1% усилия в колонне при одновременном действии до 6 колонн и 0,67% при действии более 12 колонн. Рекомендации норм ГДР приведены на рис. 13.3, б пунктиром.

Данные о величинах углов перелома колонн справедливы для случая «свободного» монтажа каркаса, т. е. когда установка и выверка каждой колонны производятся независимо от других колонн здания. «Принудительный» монтаж при помощи кондукторов с фиксированной привязкой каждой очередной колонны к смонтированной ранее части каркаса дает, как показал опыт, другие, значительно меньшие, величины углов перелома⁴.

Определение усилий в элементах дисков перекрытий от переломов осей колонн иллюстрируется следующим примером расчета простейшего диска (рис. 13.3, в). Диск образован расположенными по осям колонн ригелями в поперечном и распорками в продольном направлении, способными воспринимать горизонтальные силы любого знака. Промежутки между ригелями и распорками заполнены настилами, воспринимающими только сжимающие и сдвигающие горизонтальные усилия. Опорами диска служат две поперечные и одна продольная стена жесткости. Нормальная ,сила во всех колоннах в уровне рассматриваемого диска N = 600 Т.

В поперечном направлении на консольную часть диска одновременно действует шесть колонн. По графику на рис. 13.3, б для шести колонн ε₆=0,0066. Горизонтальная нагрузка от каждой колонны


Расчетная схема и усилия в диске приведены на рис. 13.3, г.

На участке диска, расположенном между стенками жесткости, в поперечном направлении оказывает влияние . одновременное действие 21 колонны. Для этого случая ε₂₁=0,0044 и Т₂₁=600·0,0044=2,64 Т.

Приведенные схемы загружения диска дают наибольшие растягивающие усилия в распорках ряда В от поперечных переломов колонн:


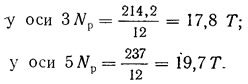
Переломы колонн в продольном направлении также вызывают растягивающие усилия в распорках. Для получения наибольшего растягивающего усилия в распорке у оси 3 ряда В следует учесть одновременное влияние поперечных переломов шести колонн по осям 1 и 2 и продольных переломов трех колонн по осям 1, 2 и 3 ряда В, т. е. учесть воздействие девяти переломов. При этом ε₉=0,0058 и Т₉=600·0,0058=3,48 Т.

Растягивающее усилие в распорке у оси 3 будет равно:


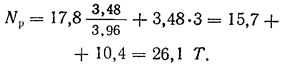
Для распорок у оси 5 ряда В в дополнение к поперечным переломам нужно учесть продольные переломы колонн ряда В, направленные влево у колонн, расположенных левее оси 5, и вправо — правее оси 5. При этом будет учтено влияние 29 колонн и ε₂₉=0,0039; Т₂₉=600·0,0039=2,34 Т;


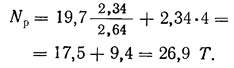
Сдвигающее усилие в диске по схеме на рис. 13.3, г при поперечной силе между осями 2 и 3 Q=23,8 Т составит:


Каждая фасадная колонна должна быть прикреплена к диску на усилие от перелома одной колонны:


Способом, приведенным выше, могут быть определены усилия в любом из элементов диска перекрытия от переломов осей колонн. Естественно, что для каждого элемента должна быть подобрана расчетная комбинация переломов. Усилия от переломов колонн должны быть; просуммированы с усилиями от ветровой нагрузки и других воздействий на диски; перекрытий.

Исходя из обобщения фактических отклонений (переломов) колонн на зданиях института Гидропроект, а также зданий с унифицированным каркасом — гостиницы «Националь» и административных зданий на проспекте Калинина, на основе полученных по этим отклонениям усилий расчетные растягивающие усилия на элементы перекрытий унифицированного каркаса приняты: для ригеля — 20 Т, для настила-распорки — 30 Т⁵.

Расчет дисков перекрытий на горизонтальные усилия — ветровую нагрузку и нагрузку от перелома колонн — производится как балочной конструкции.

В простейшем случае, когда в плане здания имеются три стены жесткости (две поперечных и одна продольная или наоборот), диски перекрытий являются статически определимыми. В этом случае реакции стен жесткости и усилия в дисках от любых нагрузок определяются из статических условий равновесия.

В более сложных случаях, когда здание имеет систему поперечных стен жесткости, диски статически неопределимы. Большая жесткость дисков перекрытий позволяет определять усилия в них от ветровой нагрузки, как в абсолютно жестких балках на упругих опорах-стенах жесткости. Задача по определению опорных реакций стен жесткости от ветровой нагрузки при решении ее методом перемещений сводится к определению двух неизвестных — смещения и угла поворота диска при любом числе поперечных стен жесткости.

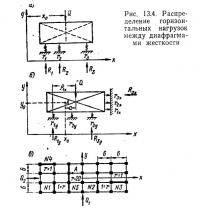
Рассмотрим какой-либо абсолютно жесткий диск перекрытия, упругими опорами для которого служат диафрагмы жесткости (рис. 13.4, а). Реакции опор обозначим через R₁, R₂, R₃. Предполагая, что реакции опор пропорциональны их перемещениям, запишем:


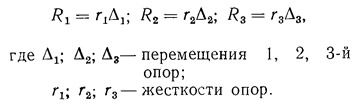
Если диск перекрытия перемещается поступательно, то Δ₁=Δ₂=Δ₃=Δh, в связи с чем


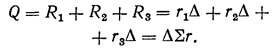
Отсюда находим горизонтальное поступательное перемещение данного диска перекрытия:


Зная величину Δ, находим искомые реакции опор:


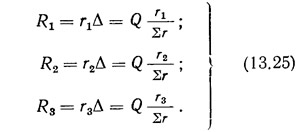
Предположение о поступательном перемещении диска перекрытия будет справедливо, если сумма моментов всех сил, действующих на данный диск относительно любой точки, равна нулю (см. рис. 13.4, а):


откуда

где

Полученная координата х₀ представляет собой координату центра кручения. Аналогично можно получить координату центра кручения оси у. В итоге будем иметь:


где r_y — жесткость диафрагм, расположенных вдоль оси у; r_x — жесткость диафрагм, расположенных вдоль оси х (рис. 13.4, б).

Если равнодействующая ветровой нагрузки не проходит через центр кручения, то возникает крутящий момент, поворачивающий диски перекрытий, который разгружает одни вертикальные диафрагмы и догружает другие. Величина дополнительных сил, действующих на вертикальные диафрагмы от крутящего момента, может быть найдена следующим образом.

Составляем уравнение моментов:

Обозначая через φ угол закручивания диска, получаем перемещения (деформации) опор: Δ₁=φρ₁; Δ₂=φρ₂ и т. д., как для диафрагм, расположенных вдоль оси х, так и вдоль оси у. Следовательно,


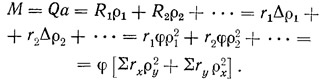
Вводя понятие крутильной жесткости

получаем угол закручивания

где М=Qa.

Усилия в упругих опорах диска от крутящего момента определяются выражением


или

где R_i — дополнительное усилие в опоре i от крутящего момента M=Qa; r_i — жесткость связи i.

В этой формуле принимается знак плюс, если дополнительное перемещение от крутящего момента направлено в сторону поступательного перемещения диска от действия силы Q, проходящей через центр кручения, и знак минус, если перемещение направлено в обратную сторону.

Полное усилие в каждой упругой опоре определяется выражением


где первый член представляет собой реакцию от поступательного перемещения диска, а второй — от его поворота.

В первом слагаемом r берется для вертикальных диафрагм, расположенных либо вдоль оси х, либо вдоль оси у, а во втором слагаемом при подсчете величины с учитываются все продольные и поперечные диафрагмы.

Пример. Требуется распределить горизонтальную ветровую нагрузку на диафрагмы, план которых изображен на рис. 13.4, в. На этом же рисунке даны относительные жесткости диафрагм.

Находим координаты центра кручения относительно осей х и у:


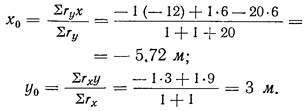
При действии силы Q₁ и при поступательном перемещении диска вдоль оси у усилия, действующие на диафрагмы 1, 2, 5, равны:


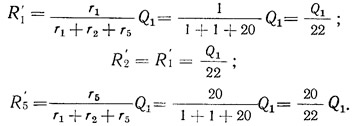
Для определения дополнительных усилий от крутящего момента M=Q₁a=Q₁·5,72 находим жесткость на кручение всех диафрагм, для чего предварительно определяем расстояние от каждой диафрагмы до центра кручения:


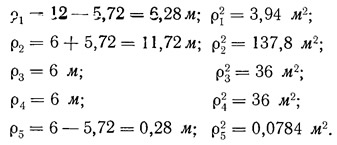
Жесткость на кручение всего диска

Дополнительное усилие для диафрагмы № 1 от крутящего момента 5,72 Q₁


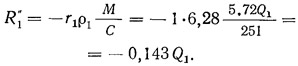
Аналогично для других диафрагм:

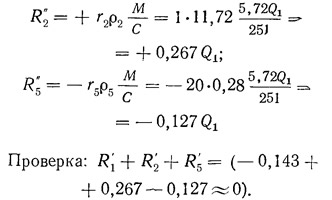
Полные силы, действующие на диафрагмы поперечного направления от силы Q₁:


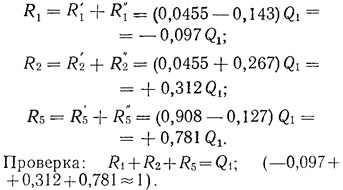
Усилия в продольных диафрагмах № 3 и 4 от крутящего момента определяются аналогично:


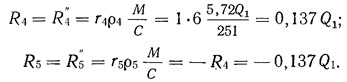
Иначе работают диски на нагрузки от переломов осей колонн. Эти нагрузки, как правило, меняют направление по высоте здания. Стены жесткости, воспринимающие реакции от дисков перекрытий, вызываемые переломами колонн, работают на восприятие этих усилий малыми пролетами, равными четырем — шести этажам. Вследствие этого жесткость опор дисков оказывается весьма большой. Сопоставительные расчеты показали, что усилия в статически неопределимых дисках перекрытий от переломов осей колонн могут определяться, как в неразрезной балке на жестких опорах.

В этом случае погрешность в определении усилий в элементах диска из-за неточности расчетной схемы в худшем случае не превысит 10—15%, что следует считать вполне приемлемым вследствие общей приближенности расчета.

Таким образом определяются поясные усилия в элементах диска и проверяется: соответствие несущей способности распорок или ригелей этим усилиям; сдвигающие силы в элементах диска и соответствие несущей способности настила и распорок по срезу шпонок этим усилиям; изгиб консолей распорок в горизонтальной плоскости; соответствие соединительных элементов диска действующим усилиям; надежность соединения дисков со стенками жесткости.

Анализируя предложенный метод определения дополнительных горизонтальных нагрузок на каркас и перекрытия от переломов колонн, которые оказываются весьма значительными и превышают величины усилий от ветровой нагрузки, следует отметить, что учет этих усилий приводит к ощутимым затратам стали на дополнительное армирование ригелей и настилов-распорок.

В связи с этим представляется, что этот расчет, основанный на приведенных выше предпосылках и заданных отклонениях колонн, приемлем только на первом этапе строительства многоэтажных каркасных зданий из сборного железобетона, когда технология монтажа полностью еще не отработана, следствием чего и являются повышенные отклонения колонн от вертикали.

По требованиям СНиП III-B.3-62 для сборных железобетонных конструкций отклонение осей колонн от вертикали должно быть не более 0,001 H, что при высоте колонны 6 м составляет 6 мм, а не 30 мм, как принято в расчете.

Таким образом, после отработки технологии монтажа и обеспечения в результате этого заданных СНиП жестких допусков, абсолютная величина горизонтальных усилий на диски перекрытий от переломов колонн должна быть значительно снижена.

3. Расчет вертикальных диафрагм жесткости

Определение нагрузок на диафрагмы в предположении абсолютной жесткости дисков перекрытий приведено выше — в расчете дисков перекрытий на ветровую нагрузку.

По статической схеме сплошная диафрагма жесткости — это консоль, для которой изгибающие моменты и поперечные силы вычисляются элементарно по методам сопротивления материалов.

Сечения стен жесткости загружены нормальной силой, изгибающим моментом и поперечной силой. Нормальные сечения проверяются в соответствии с требованиями СНиП II-B.1-62, как внецентренно сжатые железобетонные элементы (случай малых эксцентрицитетов. Проверка производится по формуле Ne<∑(R_прS_б+R_aS_a) и на сдвиг по формуле Q≤R_pF_ст.

Возможность совместной работы колонн и стенки в предельном состоянии должна обеспечиваться при сборных диафрагмах надежными связями между стенами жесткости и колоннами.

В связевых диафрагмах, расположенных перпендикулярно рамам каркаса, вертикальная нагрузка от перекрытий передается ригелями каркаса непосредственно на связевые колонны.

В дальнейшем происходит перераспределение вертикальных усилий между колоннами и стенками жесткости, в связи с чем здесь возникают сдвигающие усилия, распределение которых по высоте здания носит сложный характер.

На величину сдвигающих усилий оказывает влияние податливость закладных деталей, различная деформативность стыков колонн и горизонтальных стыков стенок жесткости и т. п.

Суммарное сдвигающее усилие, на которое должны быть рассчитаны эти связи, складывается из усилия Т_N1, передаваемого с колонны на стенку, и усилия Т_в от действия горизонтальной нагрузки. Усилия T_N1 можно определить по формуле


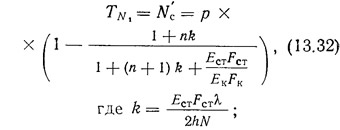
p — нагрузка по грузовой площади, отнесенная к единице высоты диафрагмы, т. е. p=N/x, где х — отсчитываемая сверху координата рассматриваемого сечения диафрагмы.

Исходя из равенства деформаций сжатия колонн и стенки диафрагмы и учитывая, что при двухэтажных колоннах каждому стыку колонн соответствует n горизонтальных стыков в стенке, получим усилие, воспринимаемое колонной в связевой диафрагме (т. е. при учете участия стенки в работе колонны),


∑N — усилие (по грузовой площади) в обеих колоннах, примыкающих к стенке диафрагмы; δ — толщина стенки; λ — деформация обжатия в горизонтальном стыке, принимаемая по СНиП П-В.1-62, в швах, заполненных раствором, равной 1 мм, а в сухих швах — 0,5 мм.

Возможно также с достаточной для практических целей точностью определять усилие между стенкой и колонной (рис. 13.5) в связевых диафрагмах упрощенным способом. (Рекомендуемый выше метод распределения нагрузок между колоннами и стенкой также является в значительной мере условным, так как условны величины жесткости колонн, диафрагм и деформативность стыков и соединений.)

Напряжения в каком-либо сечении сплошной вертикальной диафрагмы (рис. 13.5,6) могут быть определены по формуле


где N — нормальная сила в данном сечении; М — изгибающий момент; у — расстояние от центра тяжести приведенного сечения диафрагмы до рассматриваемого волокна; F_прив; J_прив — приведенные площадь и момент инерции сечения.

Для сборных диафрагм учет податливости соединений и повышение в связи с этим напряжений и деформаций могут быть произведены приближенно путем уменьшения приведенной площади F_прив и приведенного момента инерции сечения J_прив на определенную величину, например:


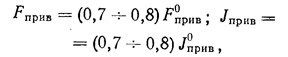
где F⁰_прив и J⁰_прив — приведенные площадь и момент инерции сечения, вычисленные без учета податливости соединений. Коэффициент 0,7—0,8 — условная величина и подлежит уточнению путем эксперимента.

После определения напряжений могут быть определены усилия в элементах диафрагмы умножением вычисленного напряжения на приведенную площадь.

Кроме определения нормальных напряжений по формуле (13.34) рекомендуется определять также главные растягивающие напряжения


где σ — вертикальное нормальное напряжение в какой-либо точке диафрагмы (сжатие «+», растяжение «—»); τ — касательное напряжение в этом же месте:


здесь Q — поперечная сила в сечении диафрагмы; S — статический момент части площади сечения диафрагмы, расположенной дальше рассматриваемого слоя, относительно нейтральной оси сечения диафрагмы (приведенный); b — толщина стенки.

Устройство сплошных стен жесткости не всегда оказывается практически осуществимым. Часто приходится применять стены жесткости, ослабленные проемами, которые расчленяют диафрагму на отдельные ветви.

При действии внешней нагрузки перемычки над проемами, являющиеся по своей статической работе упругими связями между ветвями, препятствуют взаимному повороту и смещению ветвей диафрагм. При этом чем больше жесткость перемычек, тем меньше сказывается ослабляющее влияние проемов. В предельном случае, когда перемычки абсолютно жесткие, диафрагма работает как сплошной консольный брус и, наоборот, когда жесткость перемычек ничтожно мала, каждая ветвь диафрагмы работает как самостоятельная консоль.

Способ определения усилий в элементах диафрагм с проемами зависит от соотношения жесткостей пилонов и перемычек. Это соотношение для диафрагмы, состоящей из двух пилонов, соединенных перемычками (рис. 13.6), проф. А. Р. Ржаницын характеризует безразмерным параметром β:


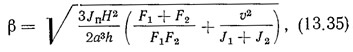
где J_п — момент инерции перемычки; J₁ и J₂ — моменты инерции пилонов; Н — высота диафрагмы; h — высота этажа; а — половина ширины проема; v — расстояние между центрами тяжести пилотов.

При β≥15 податливость перемычек мала и диафрагма работает как единое сечение и рассчитывается по консольной схеме. При β≤0,55 податливость перемычек велика и их влияние на работу пилонов несущественно; пилоны диафрагмы работают раздельно и рассчитываются как отдельные самостоятельные консоли. При промежуточных значениях 15>β>0,5 характер работы диафрагмы с проемами напоминает работу рамы. В этом случае усилия в элементах диафрагм могут определяться, как в рамных системах.

Расчет диафрагм, ослабленных регулярными проемами, при условии приведения расчетной схемы к рамной системе удобно выполнять с использованием электронной вычислительной техники (см. ниже). Возможно также использование целой серии приближенных способов расчета диафрагм, ослабленных проемами. Эти способы изложены в работах А. Р. Ржаницына, С. В. Полякова, А. С. Калманка, П. Ф. Дроздова, Л. Е. Линовича и других авторов.

Учитывая, что диафрагмы жесткости представляют собой наиболее ответственные элементы конструкции каркаса, во многом определяющие общую надежность сооружения, его конструктивные и экономические качества, остановимся более подробно на расчете диафрагм.

В главе 8 при рассмотрении расчета несущих стен, ослабленных проемами, приведена методика, которая полностью может быть использована для расчета связевых диафрагм. Ниже приводится достаточно простой и достоверный метод расчета диафрагм, ослабленных регулярно расположенными проемами, предложенный А. Р. Ржаницыным, и выполненные в Моспроекте в развитие этого метода дальнейшие упрощения, благодаря которым удалось получить готовые табличные значения для определения ряда величин, что позволяет избежать громоздких и трудоемких вычислений.

4. Расчет диафрагм с проемами по методу А. Р. Ржаницына

В основу метода расчета диафрагм положены следующие предпосылки: диафрагма жестко заделана в фундаменте; диафрагма является упругим телом с жесткими соединениями ее элементов; ползучесть материала учитывается косвенно путем введения в расчет соответствующих жесткостей элементов; сечения диафрагмы одинаковы по высоте; ригели диафрагмы (перемычки) нерастяжимые и работают в основном на изгиб; вертикальная нагрузка принимается постоянной по всей высоте диафрагмы. Неодинаковая по высоте ветровая нагрузка заменяется эквивалентной по изгибающему моменту равномерно распределенной, что незначительно снижает точность расчета.

Рассматриваемый метод основан на замене перемычек непрерывно распределенными по высоте связями, эквивалентными по своему действию перемычкам. Закон плоских сечений в составной диафрагме нарушается; он остается справедливым только для отдельных ветвей.

Диафрагма с проемами подобна многоэтажной раме с ригелями-перемычками. За неизвестные удобно принять поперечные силы в перемычках или суммарную величину этих сил, начиная сверху, в каком-либо сечении. Зная поперечные силы в перемычках, легко найти усилия в любом сечении диафрагмы, прогибы и повороты, так как задача становится статически определимой.


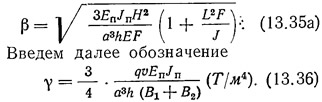
Можно дать выражение для определения поперечной силы в перемычках:


где q_п — средняя в пределах данного этажа вертикальная погонная касательная сила в Т/м:


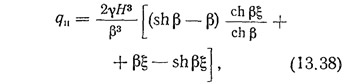
где ξ=x/H — отношение расстояния от рассматриваемого сечения до верха диафрагмы к высоте диафрагмы.

В месте заделки диафрагмы в фундамент ξ=1, следовательно,


где q — равномерно распределенная по высоте эквивалентная ветровая нагрузка в Т/пог. м (рис. 13.6, a); B₁ и В₂ — изгибная жесткость каждого пилона относительно своей собственной оси, проходящей через центр тяжести сечения каждого пилона (ц. т.):


L₁ и L₂ — расстояния от середины перемычки до центров тяжести пилонов:


а — половина длины перемычки; J₁ и J₂ — моменты инерции каждого пилона относительно своей собственной оси; Е_п и Е — модули упругости соответственно ригеля (перемычки) и диафрагмы; F₁ и F₂ — площади сечения пилонов диафрагмы.

Характер изменения поперечных сил в перемычках при 0,5≤β≤15 показан на рис. 13.6, б.

Прогиб диафрагмы в любом сечении определяется выражением


Суммарная вертикальная сдвигающая сила в шве в любом сечении диафрагмы, равная сумме поперечных сил во всех перемычках, расположенных выше рассматриваемого сечения,


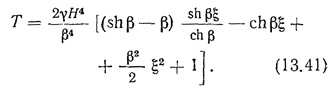
Очевидно, что нормальная продольная сила, которая действует в каждом пилоне, равна N=±T(sh β — синус гиперболический, ch β — косинус гиперболический).

Изгибающий момент, действующий на каждую ветвь диафрагмы, определяется формулами:



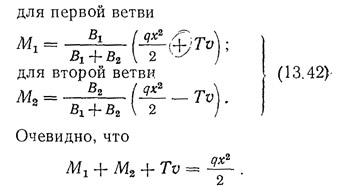
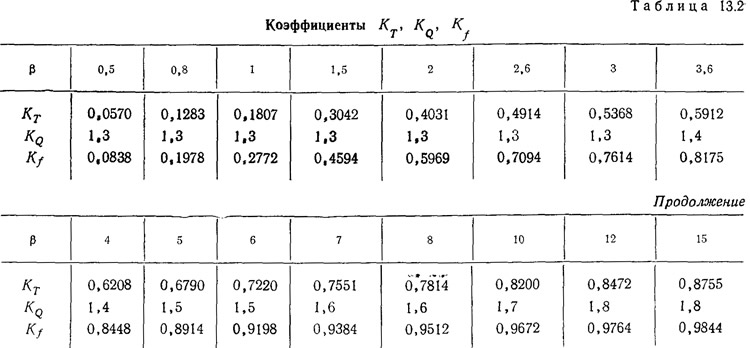
Для облегчения расчетов в табл. 13.2 приведены значения коэффициентов для вычисления величин Т и Q и прогиба f. Максимальное значение суммарной сдвигающей силы (в основании диафрагмы)


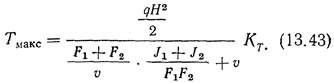
Для симметричной диафрагмы, когда F₁=F₂=F; J₁=J₂=J, это выражение принимает вид:


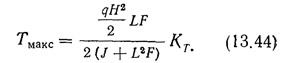
Максимальное значение поперечной силы в перемычке

Максимальный прогиб диафрагмы (наверху)

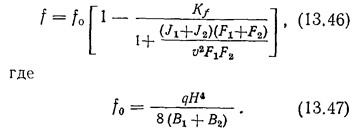
Для симметричной диафрагмы

Расчет диафрагм с одним рядом проемов при различных сочетаниях внешних нагрузок

Существующие методы расчета диафрагм с проемами достаточно трудоемки, особенно для тех случаев, когда приходится рассчитывать диафрагмы на различные виды загружений.

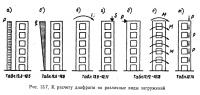
В связи с этим для практики проектирования представляют интерес предложения по упрощению техники расчетов. Ниже приводится такой метод (формулы и таблицы) расчета наиболее распространенного типа двухветвенных диафрагм на различные виды загружений (рис. 13.7), разработанный в Моспроекте⁶.

Расчетные формулы, а также таблицы коэффициентов, составленные для различных нагрузок и жесткостей диафрагм, позволяют проектировщикам достаточно быстро получить нужные величины перерезывающих и нормальных сил, изгибающего момента и горизонтального прогиба на любом уровне i=x/H диафрагмы.

Основные положения для расчета приняты в соответствии с «Теорией составных стержней строительных конструкций» А. Р. Ржаницына (1948 г.).

Расчетные величины усилий и деформаций определены методом сил. Для удобства вывода расчетных формул при составлении дифференциальных уравнений за неизвестное принят при действии внешних горизонтальных нагрузок угол поворота &teta;_pi диафрагмы.

Решение составленных уравнений выполнено на электронной вычислительной машине «Минск-22».

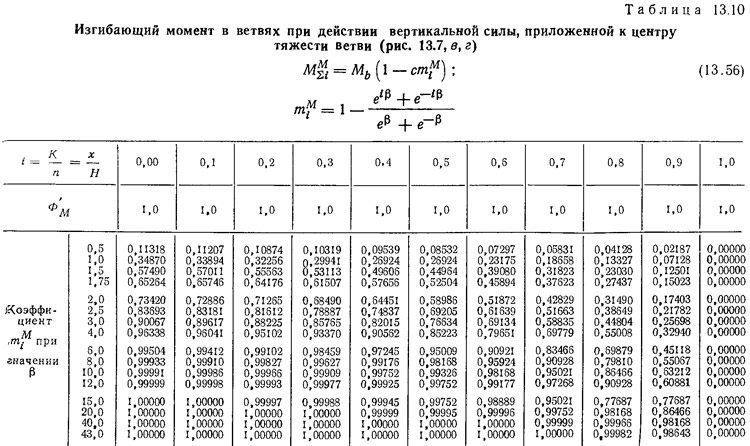
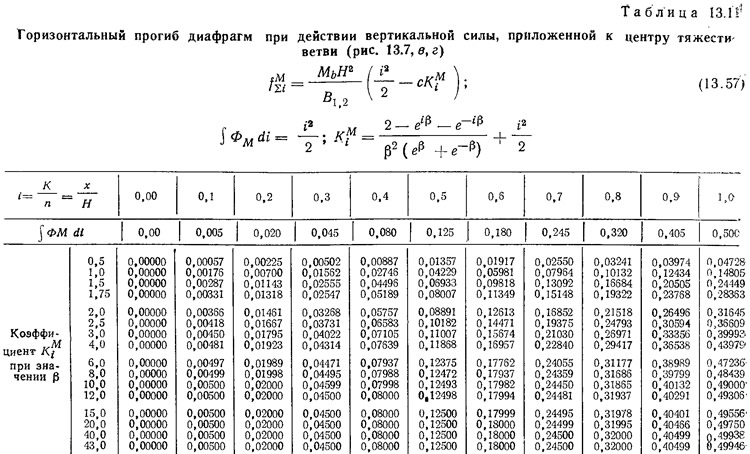
В табл. 13.3—13.4 приведены окончательные формулы и значения коэффициентов для определения величин перерезывающих сил, изгибающих моментов и прогибов двухветвенных диафрагм при различных видах внешних воздействий (см. рис. 13.7).



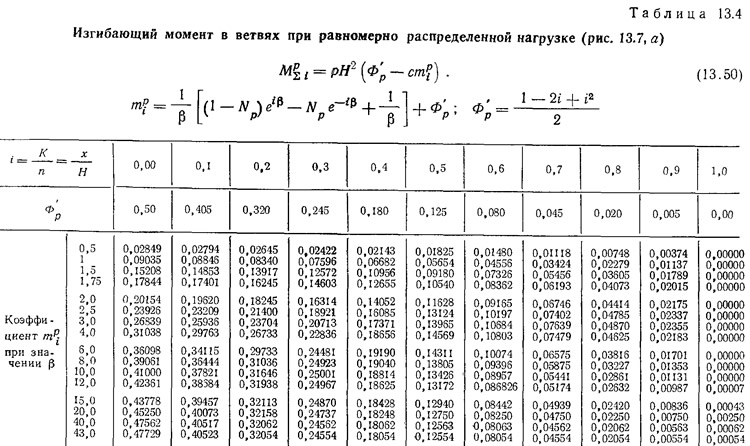
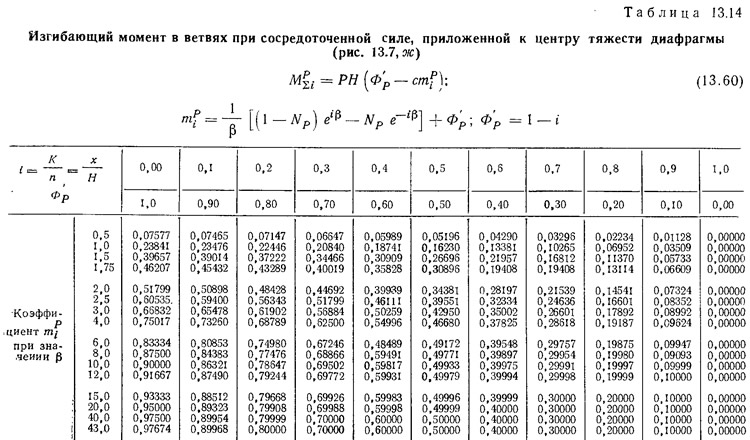
Формулы для определения усилий и деформаций при действии в одной из ветвей поэтажных вертикальных сил, приложенных к центру тяжести сечения ветви (рис. 13.7, ж):

перерезывающая сила в перемычках

изгибающий момент

прогиб верха диафрагмы

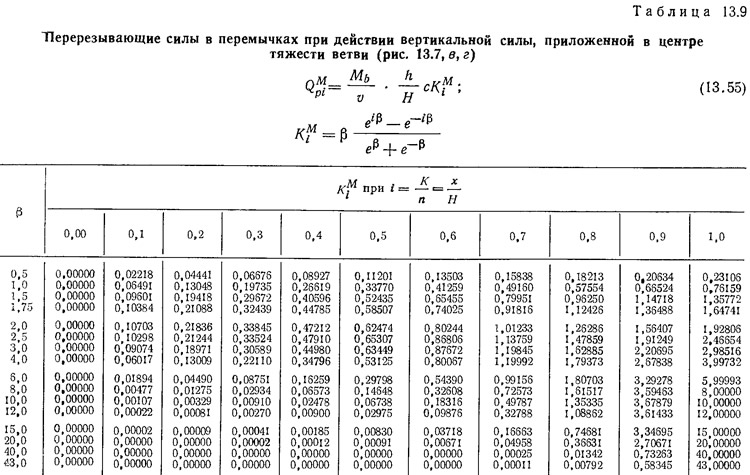
Значения расчетных коэффициентов берутся из табл. 13.9—13.11.

Формулы для определения усилий и деформаций в двухветвенной диафрагме при внешнем сосредоточенном моменте, приложенном в ее вершине (рис. 13.7, в):

перерезывающая сила в перемычках

где

изгибающий момент

прогиб верха диафрагмы

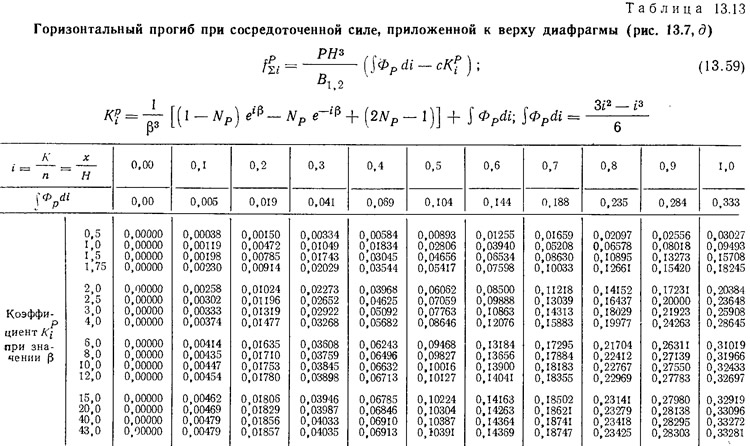
Формулы при вертикальной силе S, действующей в центре тяжести вершины одной из ветвей (рис. 13.7, г):

перерезывающая сила в перемычках

изгибающий момент

прогиб верха диафрагмы

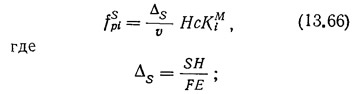
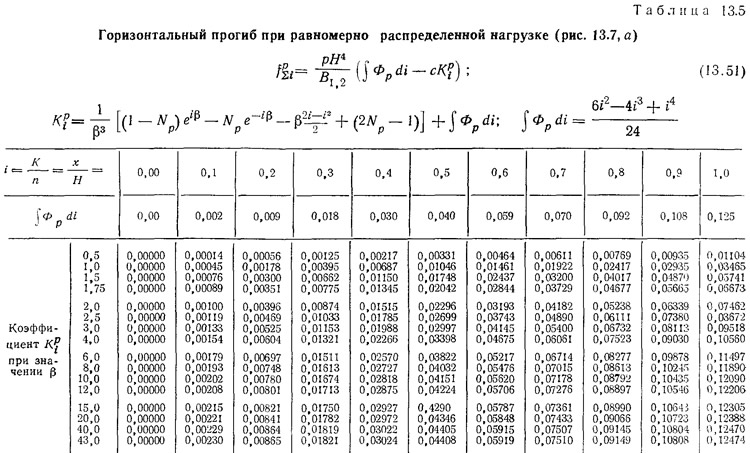
F — площадь горизонтального сечения нагруженной ветви.

Значения коэффициентов K^M_i и m^M_i приведены в табл. 13.9—13.11.

Расчет несимметричной диафрагмы

Рассмотрим методику расчета несимметричной диафрагмы (см. рис. 13.6, в). Если разрезать ригель в середине, то взаимное расхождение его конца было бы равно:


Предполагается, что деформацией сжатия пилонов можно пренебречь. Поперечные силы в ригеле Q должны совместить его концы, поэтому


где B_п=EJ_п — изгибная жесткость перемычки.

Отсюда находим формулу для определения поперечной силы в перемычке:


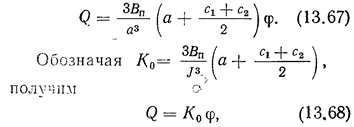
т. е. поперечная сила в перемычке опять пропорциональна углу поворота пилона.

Дальнейший ход вычислений может быть следующим. Рассматриваем пилон № 1 (см. рис. 13.6, г).


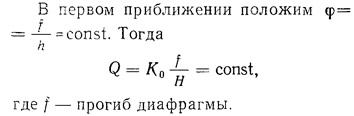
Момент, действующий на пилон № 1, от силы Q:


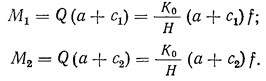
Раскладывая эти моменты на пары горизонтальных сил с плечом, равным высоте этажа h, приходим к схеме, изображенной на рис. 13.6,г). Очевидно, что


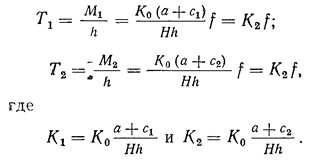
Определяем прогиб пилонов № 1 и 2 от сил, изображенных на рис. 13.6. г:


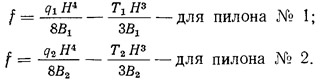
Решая эти два уравнения, находим прогиб f в первом приближении:


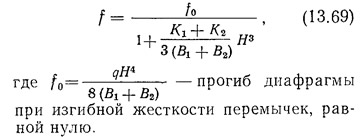
Ветровая нагрузка, передающаяся на пилоны № 1 и 2:


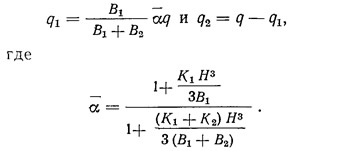
Как показывает анализ, вторые члены в знаменателе и числителе формулы для α намного больше единицы. В связи с этим можно считать, что


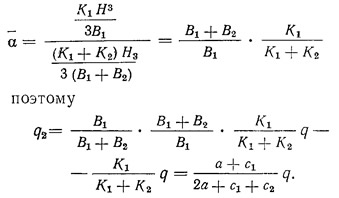
Но так как 2a+c₁+c₂=v — расстояние между осями пилонов, то


Зная нагрузки q₁ и T₁ (или q₂ и Т₂), легко найти углы поворота пилона № 1 (или № 2) и вычислить поперечные силы в перемычках во втором приближении.

Расчет диафрагмы с двумя рядами проемов

Покажем возможный порядок расчета диафрагмы с двумя рядами вертикальных проемов.

Для простоты вычислений примем, что ширина всех трех пилонов одинакова, а также равны между собой высоты перемычек. Перемычки будем считать настолько гибкими, что продольной деформацией пилонов можно пренебречь. Задачу будем решать методом последовательного приближения.

Деформированное состояние пилонов и перемычек показано на рис. 13.8, а.

Если φ — угол поворота диафрагмы в рассматриваемом месте по высоте, то усилие в перемычке, как это было показано ранее,


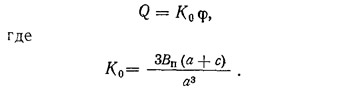
Изгибающие моменты, действующие на крайние пилоны со стороны перемычек,


Пусть в первом приближении φ=f/h=const, где f — прогиб диафрагмы. Так как при этом постоянный по высоте момент М можно разложить на пары горизонтальных сил с плечом, равным высоте этажа h, то в итоге опять получим схему, изображенную на рис. 13.8, б. Для среднего пилона, очевидно, схема эта будет выглядеть так, как показано на рис. 13.8, в.

Горизонтальная сила Т определяется выражением


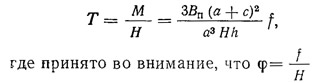
Для определения прогиба диафрагмы f и действующих на пилоны горизонтальных сил q₁ и q₂ (2q₁+q₂=q) запишем выражения прогиба пилонов:


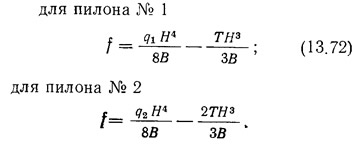
Записывая значение силы Т в форме T=rf, где


и решая два предыдущих уравнения (13.72), находим:

а) прогиб диафрагмы в первом приближении

б) нагрузки, действующие на пилоны:

Прогиб диафрагмы можно выразить также формулой


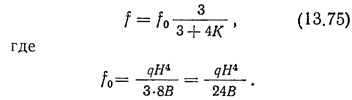
Формулы первого приближения дают, конечно, еще грубый результат, поэтому для более точного расчета следует выполнить второе приближение, т. е. найти углы поворота диафрагмы от найденных в первом приближении сил q₁, q₂, T = rf.

При этом все время нужно следить за совместностью деформаций пилонов № 1 и 2 (т. е. за равенством их прогибов).

Так как форма деформации пилонов одинаковая, то в любом сечении


где B₁, B₂, B₃ — изгибные жесткости пилонов в общем случае.

Следовательно:

т. е. изгибающие моменты в пилонах пропорциональны их жесткостям.

Если, как в нашей задаче, B₁=B₂=B₃=B, то M₁=M₂=M₃ в любом сечении.

Расчет диафрагмы с жесткими перемычками

При. высокой жесткости перемычек, когда Р> 15 [см. формулы (13.35) и (13.35а)], диафрагма практически работает как цельная балка, в которой эпюра нормальных напряжений в упругой стадии является прямолинейной.

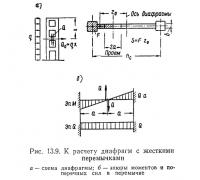
Усилия в перемычках такой диафрагмы могут быть определены из условия, что вся поперечная сила, действующая в месте проема, при рассмотрении этой диафрагмы как сплошной сосредоточивается в перемычке (рис. 13.9, а):


Так, например, если диафрагма имеет прямоугольное сечение, а проем расположен в середине сечения, то момент инерции сечения (брутто)


Статический момент площади, расположенной по одну сторону от оси, проходящей через середину проема, относительно центральной оси


Поперечная сила в перемычке, расположенной на любой высоте х от верха диафрагмы,


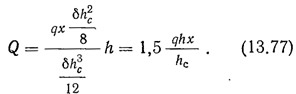
Зная усилия в перемычках, можно найти дополнительный прогиб диафрагмы, вызванный их податливостью. Для определения дополнительного прогиба прикладываем к диафрагме наверху силу, равную единице. Усилия в перемычках, возникающие от этой единичной силы,


а характер эпюры моментов такой же, как от ветровой нагрузки q (рис. 13.9, б).

Произведя перемножения грузовых и единичных эпюр, получим:


где 1,2 — коэффициент неравномерности распределения касательных напряжений в прямоугольном сечении.

Подставляя в это выражение значения сил Q и Q, получаем дополнительный прогиб диафрагмы от податливости только одной перемычки:


Дополнительный прогиб диафрагмы от податливости всех перемычек, очевидно, равен: Δf=∑Δf_i.

Для регулярно расположенных по высоте проемов имеем:


Полный прогиб диафрагмы с проемами определяется выражением


где f₀ — прогиб диафрагмы в предположении отсутствия проемов:


J — момент инерции сечения диафрагмы брутто;
Δf — дополнительный прогиб диафрагмы от податливости перемычек.

Полученными формулами можно пользоваться в том случае, если дополнительный прогиб Δf не превышает 20—30% основного прогиба Δf, так как в противном случае распределение поперечных сил в перемычках существенно отличается от того закона, который принят при выводе.

Влияние касательных напряжений (поперечных сил) на распределение усилий в диафрагме

Обычно при определении деформаций балок влиянием поперечных сил, создаваемых касательными напряжениями в сечениях, пренебрегают. Однако при расчете вертикальных диафрагм жесткости, характерной особенностью которых является относительно большая высота сечения, пренебрегать влиянием на деформации касательных напряжений в ряде случаев нельзя.

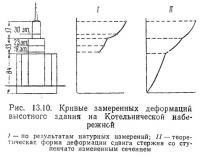
Замеренные в натуре формы колебаний ряда высотных зданий, построенных в Москве, убедительно показывают, что преобладающее влияние на прогиб здания оказывают сдвиговые деформации (рис. 13.10).

Прогиб консольной балки прямоугольного сечения, находящейся под действием сосредоточенной силы Р (рис. 13.11, а), равен:


Первый член этой формулы дает изгибную деформацию, второй — сдвиговую.

Формулу (13.81) запишем в виде:

Таким образом, если длина рассматриваемой консольной балки прямоугольного сечения не превышает 2,5 высоты сечения балки, то необходимо учитывать влияние касательных напряжений на деформацию балки.

Так как перемычки диафрагм жесткости работают по описанной здесь схеме, то к ним в полной мере применим этот вывод. Для простоты вычислений можно учесть сдвиговую деформацию путем использования эквивалентной жесткости:


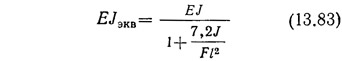
и подставлять эту величину во все формулы, где фигурирует жесткость EJ.

Рассмотрим другую схему загрузки консольной балки равномерно распределенной нагрузкой q (рис. 13.11, б).

На рис. 13.11, в даны грузовая и единичная эпюры поперечных сил. Перемножая эти эпюры, получаем прогиб конца балки от поперечных сил:


где коэффициент неравномерности касательных напряжений принят равным 1,2.

Полный прогиб

Эквивалентная жесткость для данного случая


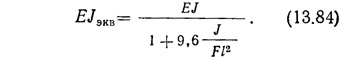
При расчете вертикальных диафрагм жесткости повышенная деформативность пилонов вследствие сдвига может быть учтена путем введения в расчет этой эквивалентной жесткости.

Чем меньше жесткость пилонов, тем выше усилия в перемычках, поэтому учет сдвиговой деформации пилонов приводит к получению более высоких усилий в перемычках.

5. Расчет колонн каркаса

В связевом каркасе колонны воспринимают нормальные силы и относительно небольшие изгибающие моменты, возникающие от опорных моментов ригелей и вследствие общих деформаций здания. Последним фактором обычно пренебрегают.

Расчетную схему колонны можно представить как многопролетную балку, к которой кроме нормальных сил и изгибающих моментов в узлах приложены еще в стыках сосредоточенные силы от переломов колонн и моменты от эксцентрицитетов в стыках. Этот случайный эксцентрицитет принимается равным 2 см.

Колонны рассчитываются на косое внецентренное сжатие. Нагрузка от ригелей данного этажа считается приложенной с эксцентрицитетом


Расчетный эксцентрицитет в плоскости рамы


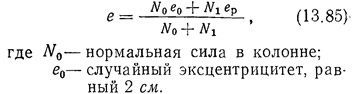
Проверка прочности колонн с гибкой арматурой и их стыков выполняется обычными способами, изложенными в СНиП II-B.1-62.

Рекомендации по расчету колонн с металлическими сердечниками в литературе отсутствуют. В практике проектирования несущую способность колонн с сердечником вычисляют, как сумму несущих способностей всех элементов сечения по формуле


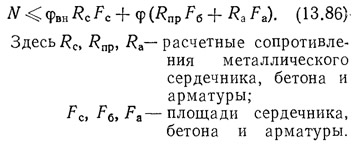
Коэффициенты снижения несущей способности при продольном изгибе φ_вн и φ принимаются по соответствующим таблицам в зависимости от гибкости приведенного сечения:


Момент инерции и площадь приведенного сечения колонны (J_прив и F_прив) вычисляются с учетом соотношения модулей упругости элементов сечения. Влияние ползучести бетона учитывается при вычислении приведенных геометрических характеристик сечения снижением начального модуля упругости бетона примерно в 3 раза.

Этот способ проверки прочности колонн с сердечником экспериментально не проверен и является предварительным. Вследствие этого в строящихся зданиях сечения колонн с сердечником назначаются с некоторым дополнительным запасом.

6. Применение электронной вычислительной техники для расчета каркаса

В классических методах строительной механики в настоящее время происходят серьезные изменения, связанные с внедрением в проектирование электронной вычислительной техники.

Пересмотру подвергаются такие принципиальные вопросы, как выбор расчетной схемы и методов расчета.

Электронные машины позволяют перейти на качественно новую ступень проектирования строительных конструкций, в том числе и многоэтажных зданий, полнее учесть физические свойства материалов конструкций, характер деформаций, перейти к расчету пространственных систем.

Работу вертикальных диафрагм жесткости многоэтажных зданий на действие горизонтальных нагрузок наиболее правильно рассматривать как работу балки-стенки, ослабленной проемами (наиболее общий случай). Но, учитывая, что теоретическое решение этой задачи сложно, чаще всего вертикальные диафрагмы с проемами рассматриваются как многоэтажные стержневые рамные системы, работающие в упругой стадии, у которых стойками являются простенки диафрагм, а ригелями — перемычки, монолитно связанные с простенками.

Имеющиеся способы расчета многоэтажных диафрагм с проемами достаточно трудоемки, причем трудоемкость вычислений возрастает с увеличением этажности здания. Большое разнообразие применяемых в строительной механике методов расчета таких конструкций объясняется стремлением найти путь с минимальным объемом вычислений. Данное обстоятельство, столь важное при ручных методах расчета, является второстепенным при использовании электронных вычислительных машин. Вот почему, например, статический расчет вертикальных диафрагм с проемами целесообразно выполнять классическим методом строительной механики — методом сил. Этим методом в Моспроекте выполнено большое количество расчетов диафрагм с проемами многоэтажных зданий на электронных вычислительных машинах БЭСМ-2М и «Минск-2» по программе СМ-4. Анализ выполненных расчетов показал, в частности, что в диафрагмах с большим числом рядов проемов, рассчитываемых как многоэтажные многопролетные рамные системы, продольные деформации простенков от нормальных сил не оказывают значительного влияния на величину усилий М, N, Q. Для таких систем удобно использовать программу СПДР-3 при работе на БЭСМ-2М, по которой при определении деформаций сооружения учитывается только влияние изгибной жесткости.

В диафрагмах с одним или двумя рядами проемов влияние продольных деформаций простенков значительно, происходит увеличение изгибающих моментов в стойках-простенках и уменьшение в перемычках-ригелях.

Аналогично решается задача расчета несущих панельных стен, которые рассматриваются как дискретные стержневые системы.

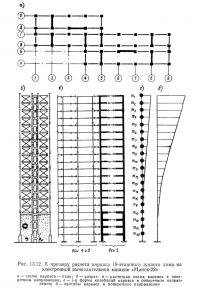
Принцип расчета рамно-связевых и рамных систем многоэтажных каркасных зданий изложен на примере расчета 19-этажного жилого дома (рис. 13.12)⁷.

19-этажный жилой дом запроектирован на базе унифицированного каркаса серии 1МГ-601Д (см. рис. 13.12, а). Здание как в поперечном, так и в продольном направлении представляет собой сложную статически неопределимую систему. Плоские конструкции здания представляют собой рамные (оси 1 ш 9 в поперечном направлении и оси А, В, Г, Е в продольном), рамно-связевые (оси 4 и 5 в поперечном направлении и Б, Д в продольном) и, наконец, связевые системы (оси 2 и 5 в поперечном направлении).

Таким образом, конструктивную основу здания составляют вертикальные связевые диафрагмы в виде железобетонных стен и рамный каркас, работающие совместно на восприятие горизонтальных ветровых нагрузок.

В расчете приняты следующие допущения: диски в уровне перекрытий являются абсолютно жесткими; ветвь диафрагмы жесткости и колонны, примыкающие к ней, в расчете учитывались как единое составное двутавровое сечение.

Основные этапы расчета

Первый этап. Определяется расчетная ветровая нагрузка на все здание в заданном направлении по формуле


Для этого к каждому ярусу каждой плоской системы прикладываются единичные силы. Полученные обратные силы перемещений составляют матрицы жесткостей плоских систем. Имея жесткость сооружения в заданном направлении, из решения характеристического уравнения определяются динамические характеристики здания. Так, период свободных колебаний здания в поперечном направлении равен T=1,93 сек, соответственно коэффициент динамичности ξ=1,8.

Второй этап. Расчетная ветровая нагрузка распределяется по связевым системам пропорционально их жесткостям.

Использование ЭВМ дало возможность для данной конструктивной схемы здания оценить точность различных методов распределения расчетной ветровой нагрузки пропорционально жесткостям по плоским системам: распределение пропорционально жесткости в верхнем ярусе от силы, приложенной там же; распределение пропорционально жесткости в каждом ярусе от силы, приложенной в верхнем ярусе; распределение пропорционально жесткости в каждом ярусе от сил, приложенных по всем ярусам (полная матрица жесткостей).

Третий этап. Выполняется расчет плоских систем на ветровую нагрузку, приходящуюся на данную систему по одной из типовых программ ЭВМ. Расчетные усилия для плоских систем получены точным методом строительной механики с учетом деформаций от изгиба и сдвига, а также от продольных деформаций.

В результате многовариантного расчета в поперечном направлении удалось подобрать жесткость плоских систем таким образом, что оказалось возможным применять без усиления типовые элементы сборного каркаса для торцовых рамных систем (оси 1 и 9) для всех 19 этажей.

Четвертый этап. Выполняется расчет здания в продольном направлении на постоянную, временную и ветровую нагрузки. Поскольку здание представляет собой сложную многократную стати-, чески неопределимую комбинированную систему, то для правильной оценки деформативности сооружения были приняты три варианта расчетной схемы:

• а) в первом варианте при расчете на ветровую нагрузку учитывалась только жесткость продольных рам по осям А, Б, В, Г, Д, Е; при этом расчетный максимальный прогиб верха сооружений составил 1,88 см, период свободных колебаний Т=1,52 сек;
• б) во втором (основном) варианте учитывалась совместная работа рам по осям А, В, Г, Е и диафрагм с рамами по осям Д и Б; максимальный прогиб верха сооружения составил в этом случае 1,28 см; период свободных колебаний Т=1,94 сек;
• в) в третьем варианте принята связе-вая система, состоящая только из двух продольных диафрагм жесткости по осям Б и Д. В этом случае максимальный прогиб верха сооружения составил 11,6 см. Период свободных колебаний сооружения Т=5,23 сек.

Анализ расчетов по второму и третьему варианту наглядно показал, в каких пределах находятся расчетные величины деформаций сооружения при том или ином выборе расчетной схемы.

При рассмотрении всех плоских систем в продольном направлении наиболее нагруженными являются рамные системы по осям А, Е. Проведенный расчет показал, что усилия от вертикальной и ветровой нагрузки в узлах не превышают несущей способности узлов сборного железобетонного каркаса.

За последние годы разработано большое количество программ, которые успешно могут быть использованы для расчета конструкций многоэтажных зданий. Так, программа СМ-4 для ЭВМ «Минск-2» предназначена для автоматического расчета методом сил любых плоских стержневых систем с числом неизвестных до 81. В соответствии с программой автоматизируются следующие этапы работы: определение геометрических размеров элементов конструкций (часть геометрических размеров задается); определение усилий в элементах основной системы; вычисление коэффициентов и свободных членов канонических уравнений; решение систем канонических уравнений; вычисление усилий в элементах; определение деформации сооружения. Следует, однако, отметить, что ввиду количественных и качественных ограничений программы СМ-4, она не может полностью удовлетворить требования, предъявляемые к статическому расчету конструкций многоэтажных зданий. В связи с этим разработан вариант программы для ЭВМ «Минск-22».

Принимая во внимание, что учет динамического воздействия порывов ветра на многоэтажное здание, в зависимости от частоты и формы его свободных горизонтальных колебаний, является весьма трудоемким, в Моспроекте составлена программа В-1 по определению расчетной ветровой нагрузки для многоэтажных каркасных зданий.

Эта программа позволяет определить расчетную ветровую нагрузку на сооружение в целом; распределить ветровую нагрузку по отдельным плоским системам пропорционально их жесткостям; получить усилия М, N, Q от ветровой нагрузки по каждой плоскости конструкции; получить прогиб верха сооружения от расчетной ветровой нагрузки.

Заслуживает внимания при расчете стержневых систем применение метода энергий, так как большинство задач расчета упругих систем можно свести к отысканию минимума энергии. Программа МАРОС-100 для ЭВМ «Минск-2» (машинный автоматизированный расчет стержневых систем), основанная на применении условно-экстремального принципа, применима для расчета стержневых конструкций многоэтажных зданий. Для конструкции каркасных многоэтажных зданий может быть использована программа СНДР-3 (статика и динамика рам) для ЭВМ БЭСМ-2М. Программа реализует метод распределения узловых моментов (метод X. Кросса).

Дальнейшим направлением по применению ЭВМ для расчета конструкций многоэтажных зданий должен стать переход от механизации расчета отдельных частей здания к комплексному расчету сооружений в целом с учетом взаимодействия его частей.

Необходима разработка методов полной автоматизации всех этапов расчета на ЭВМ. Наряду с разработкой универсальных алгоритмов следует разработать алгоритмы частных, но важных задач с доведением решений до необходимых конечных результатов.

Одна из основных и наиболее перспективных областей применения ЭВМ — вариантное проектирование, где благодаря быстрому и достаточно точному расчету на ЭВМ ряда возможных вариантов с помощью той же машины удается выбрать оптимальный по заданным требованиям.

Примечания

1. Возможность принимать в инженерных расчетах с достаточной степенью точности линейную форму колебаний (что существенно упрощает расчет) подтверждена, в частности, проведенными в ЦНИИЭП жилища испытаниями моделей диафрагм жесткости, выполненных в 1/10 натуральной величины.

2. Таблица и методика определения ветровых нагрузок разработаны инж. М. Н. Швехманом (Моспроект).

3. Методика определения горизонтальных воздействий на каркас от перелома осей колонн и расчета каркаса на общую устойчивость разработана инж. В. В. Ханджи (Моспроект).

4. В частности обработка измерений наклонов колонн на монтаже 25-этажных зданий на проспекте Калинина, где сборка каркаса выполнялась-в кондукторах по методу принудительного монтажа, показала, что средний угол перелома колонн составляет ε=0,0045, т. е. в 2,5 раза меньше, чем в здании Гидропроекта.

5. Обработка более 20 тыс. измерений — наклонов колонн и эксцентрицитетов на монтаже каркаса 25-этажиых административных зданий на проспекте Калинина, выполненная с использованием вероятностно-статистического математического аппарата, показала, что на величину усилий в дисках значительное влияние оказывают также эксцентрицитеты в стыках колонн.

6. Работа выполнена инж. В. Е. Сно.

7. Расчет выполнен в Отделе вычислительной техники Моспроекта под руководством инж. Г. С. Клевицкого.