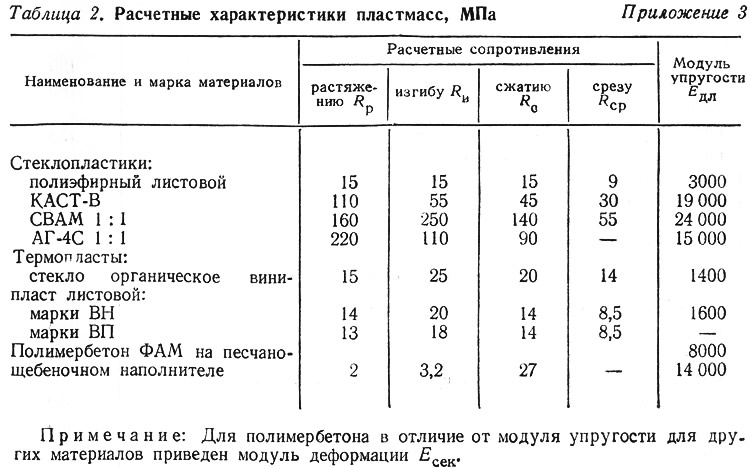
Расчет центрально-растянутых элементов
Расчет центрально-растянутых элементов по трещинообразованию для случая, когда трещин не должно быть совсем, основывается на большой растяжимости полимербетона, Предельная деформация его при растяжении (для полимербетона ФАМ) εр = 50·10-5, т. е. полимербетоны имеют значительную сопротивляемость осевому растяжению и могут применяться в строительных конструкциях без предварительного напряжения. Однако εр значительно меньше предельной растяжимости арматуры εа. При малом проценте армирования, когда арматура недозагружается, предельное состояние элемента по прочности определяется по полимербетону:
здесь Ep.сек — секущий модуль деформации при растяжении, равный 5000 МПа;
F — площадь сечения элемента;
Fa — площадь армирования.
При больших процентах армирования, если пренебречь полимербетоном, предельное состояние элемента выражается формулой
где Ra — расчетное сопротивление стали при растяжении.
Оптимальный коэффициент армирования μ0 = Fa/F находится путем приравнивания правых частей формул (46), (47) с учетом, что εрEр.сек(F—Fa) = RрFб:
здесь Rp — предел длительной трещиностойкости полимербетона (расчетное сопротивление растяжению), значение которого дано в табл. 2 приложения 3.
Площадь поперечного сечения элемента из условия (46) находится по формуле
Центрально-сжатые элементы
Их устойчивость проверяется по формуле (16), которая с учетом армирования и длительного действия нагрузки записывается так:
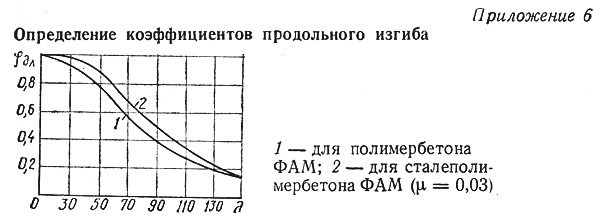
Коэффициент φдл, зависящий от гибкости и коэффициента армирования, находится по графикам приложения 6.
Изгибаемые элементы
Изгибаемые элементы рассчитываются по прочности, трещинообразованию и прогибам. В основу расчета положены следующие допущения: гипотеза плоских сечений и предположения, что эпюры нормальных напряжений по высоте сечения элемента отвечают по форме диаграммам механических испытаний на осевое сжатие и растяжение. Расчетные формулы получают составлением трех уравнений: уравнения равновесия моментов сил ∑М = 0 — первое условие; уравнения равновесия проекций сил на нейтральную плоскость ∑Р = 0 — второе условие; уравнения соотношения краевых деформаций или высот сжатой и растянутой зон поперечного сечения элемента — третье условие.
Расчет на прочность. При длительном действии нагрузок растянутая зона в восприятии нагрузки не участвует и все усилие растяжения воспринимается арматурой. В сжатой зоне эпюра напряжений соответствует квадратной параболе (рис. 45, а). Для проверки элемента по прочности, согласно первому условию, получаем
Площадь армирования Fa находим по коэффициенту армирования Fa = μbh0 (b — ширина поперечного сечения).
Коэффициент армирования сечения μ находится следующим образом. Высота сжатой зоны х находится из второго условия равновесия:
Соотношение высот сжатой зоны полимербетона и рабочей высоты сечения из условия сохранения сечением плоской формы:
Из совместного решения уравнений (52) и (53) определяется μ:
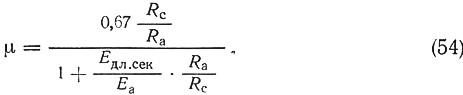
Расчет на образование трещин
При длительном действии нагрузок в результате ползучести растянутая зона элемента выключается из работы. Критерием безопасности по трещинообразованию является достижение полимербетоном предельной растяжимости в крайнем растянутом волокне ер.и (для ФАМ εр.и = 65·10-5). В этот момент деформация арматуры εа.и = εр.и(h0—x)/(h—x) (рис. 45, б). Проверка элемента производится по формуле
здесь М — расчетный момент от нормативных нагрузок.
Коэффициент армирования р находится следующим образом. При практически возможных значениях коэффициента армирования эпюра нормальных напряжений в сжатой зоне принимается треугольной. Тогда из второго условия равновесия
и из условия сохранения сечением плоской формы
Коэффициент μ определяется совместным решением уравнений (56) и (57):
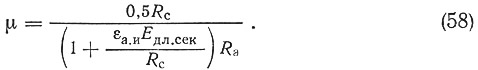
Вычисление прогибов
Прогибы балок прямоугольного сечения, рассчитываемых на трещинообразование, вычисляют по формулам сопротивления материалов в зависимости от схемы загружения. Для этого определяется жесткость расчетного сечения
где Wa = Fa (h0 — 0,33x).

