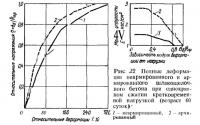
Упругопластические свойства при сжатии и растяжении для мелкозернистого бетона состава 1 обобщены на рис. 20 и 21.
Как видно из рис. 20, шлакощелочной бетон (как и портландцементный) не обладает совершенной упругостью; даже при малых кратковременных напряжениях полная деформация состоит из двух слагаемых
ε = εуп + εпл
т. е. упругой части εуп и пластической εпл. Соотношение этих частей деформаций приблизительно такое же, как и для обычного бетона.
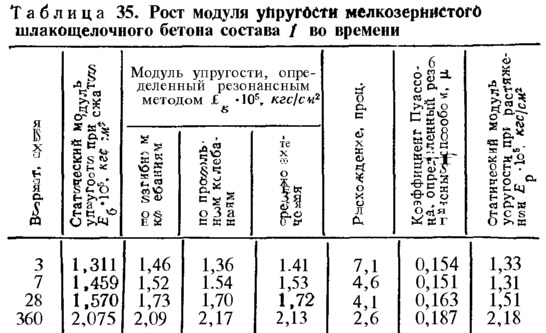
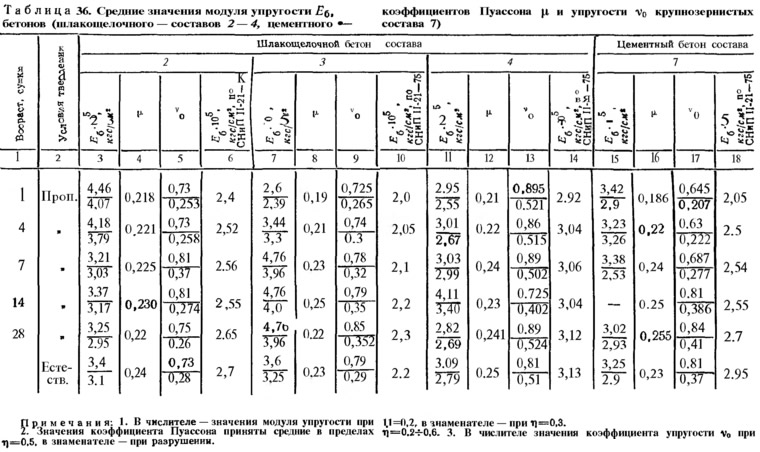
Значения модуля упругости и показатели его роста при сжатии и растяжении, в зависимости от возраста, определенные статическим и резонансным методами по изгибным и продольным колебаниям, приведены в табл. 35.
Установленные экспериментальные значения и характер изменения коэффициентов упругости v0 и Пуассона (поперечных деформаций) μ с достаточной надежностью описываются уравнением
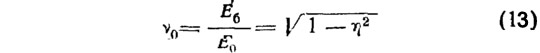
и показаны на рис. 21.
Значения коэффициента Пуассона с увеличением напряжений изменяются незначительно, в основном они близки к 0,2.
Используя закон Гука, выражение (13) и сделав незначительные преобразования, можно записать формулу для полных относительных деформаций
где εб — полные относительные деформации; η=σ/R — относительное напряжение; е0 — удельный модуль упругости; Е0 — модуль упругости бетона; R — прочность бетона, соответствующая напряженному состоянию (сжатию или растяжению, т. е. призменная прочность или прочность при растяжении).
Величину модуля упругости мелкозернистого шлакощелочного бетона при напряжениях 0,2 Rпр в зависимости от кубиковой прочности можно определять по эмпирической формуле типа Графа — Роша
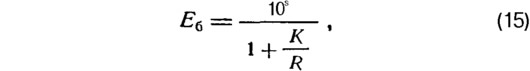
которая дает хорошие результаты при К=1800. По этой же формуле можно определять модуль упругости и для крупнозернистых бетонов, для которых коэффициент К находится в пределах 800—1200. Расхождения экспериментальных значений с теоретическими составляют 5,2—10,8%. Необходимо также отметить, что с ростом прочности (марки) удельный модуль е0 уменьшается, как и для портландцементного бетона.
Таким образом, зная значения модуля упругости и коэффициента Пуассона для шлакощелочного бетона, можно вычислить модуль сдвига G, воспользовавшись известным соотношением из теории упругости
Подставляя значения μ из табл. 35, 36, получим, что модуль сдвига изменяется в пределах (0,4—0,433) Еб.
При армировании призм 406 А = I удалось определить деформативность, модуль упругости, разрушающую нагрузку и другие параметры в различных возрастах.
На рис. 22 для сравнения приведены деформации неармированных и армированных призм. Армирование повышает упругие свойства призм и модуль их упругости примерно на 26—58%.