Двумерные температурные поля и их моделирование

Простейшие расчетные формулы распределения температур в ограждениях зданий относятся к установившимся условиям теплопередачи через плоскую и протяженную ограждающую конструкцию, обладающую теплотехнической однородностью по всей своей площади. Изменения значений температуры происходят только по поперечному сечению такой конструкции, изотермы располагаются в плане параллельно ограничивающим стену поверхностям, а распространение тепла одномерно, т. е. имеет место только в одном, нормальном к этим изотермам направлении.

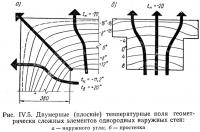
В действительности даже для однородных конструкций характерны отдельные участки с более сложным распределением температур, поскольку в здании имеются проемы, углы, пересечения стен. Условия теплообмена на притолоках простенков, в наружных углах зданий и в местах примыкания к наружным ограждениям поперечных стен или перегородок искажают простейшее температурное поле, изотермы утрачивают параллельность, а поток тепла — одномерность (рис. IV.5).

Температурное поле становится более сложным даже для простейших однородных конструкций из-за геометрического разнообразия их формы в плане.

В частности на условия теплопередачи влияет геометрическая форма наружных углов зданий. Она связана с уменьшением площади тепловосприятия и увеличением площади теплоотдачи, а также с понижением коэффициента тепловосприятия α_в из-за меньшей интенсивности конвекционных токов воздуха и лучистого теплообмена.

Температуры на внутренней поверхности угла ниже температур глади стены на 4—6°, что при отсутствии в наружных углах вертикальных труб центрального отопления приводит к отсыреванию углов, а в недостаточно отапливаемых зданиях — даже к появлению инея в наиболее холодные периоды зимы.


Устранение этих недопустимых явлений путем специального обогрева наружных углов отопительной системой связано с дополнительными потерями тепла. Распределение температур в простенках свидетельствует о сильном охлаждении поверхностей притолок, что в жилых и общественных зданиях не приводит к образованию конденсата на этих поверхностях только из-за теплоотдачи отопительных приборов и пониженного влагосодержания холодного воздуха, фильтрующегося через оконные переплеты.

Еще более сложным образом располагаются изолинии температур в сопряжениях и углах современных индустриальных конструкций.

Как уже говорилось ранее, такие конструкции часто неоднородны в теплофизическом отношении и распределение температур в их горизонтальной или вертикальной проекции выражается криволинейными изотермами, т. е., иначе говоря, является функцией от двух координат, одна из которых направлена от поверхности конструкции, обращенной в помещение, к наружной поверхности, а другая — параллельна этим поверхностям, т. е. t=f(x, у).

В гл. I указывалось, что описывающее такое распределение температуры, дифференциальное уравнение Лапласа для двумерного температурного поля (при установившемся распределении температур в однородной материальной среде), выражается в виде:


В неоднородной материальной среде дифференциальное уравнение плоского температурного поля имеет вид:


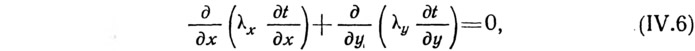
здесь λ является непрерывной функцией х и у.


Применяемый для решения уравнения (1.8а) метод конечных разностей дает возможность заменить непрерывное изменение λ — скачкообразным.

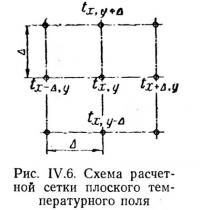
Применение метода конечных разностей обычно связано с нанесением на рассматриваемую проекцию конструкции расчетной сетки, что позволяет вычислить температуры в ее пересечениях.

Такую сетку чаще всего выбирают квадратной; желательно, чтобы стороны квадратов совпадали с поверхностью ограждения или его характерных элементов.

Сторона каждого квадрата может быть принята равной величине Δ; чем меньше эта величина, тем точнее расчет.

Направление одних линий сетки принимается параллельным, а других — перпендикулярным основному направлению потока тепла.

Уравнению (1.8а) температурного поля в однородной среде соответствует разностное уравнение


Вторые производные заменяются их выражениями через разности, а решение дифференциального уравнения сводится к решению системы обычных линейных уравнений, неизвестными в которых являются температуры в узлах сетки (рис. IV.6).

Написав подробно вторые конечные разности функции t по х и по у, получим


Решая полученное уравнение относительно t_x,y, получим:



т. е. на поверхности однородной материальной среды установившаяся температура в каждом узле сетки равна средней арифметической температуре четырех соседних узлов¹.

Формула (IV.8) справедлива только в том случае, если условия передачи тепла от рассматриваемого узла ко всем четырем, соседним с ним, одинаковы, что может иметь место только в материальной среде с одинаковой теплопроводностью во всех направлениях.

Если в рассматриваемом температурном поле имеются материалы с различной теплопроводностью, выбор расчетной сетки производится таким образом, чтобы ее узлы располагались в наиболее характерных точках поля, вычисление температуры в которых сможет установить общую закономерность распределения температур в неоднородной конструкции. Расчетная формула (IV.8) усложняется в этом случае из-за различных значений коэффициентов теплопередачи между рассматриваемой точкой и соседними.

Если в зонах передачи тепла от рассматриваемой точки к соседним, расположены материалы с различной теплопроводностью, коэффициенты теплопередачи могут быть вычислены только приближенно на основе практических методов расчета, предложенных К. Ф. Фокиным.

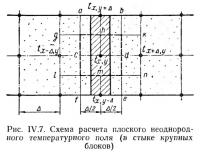
Существо этих практических методов рассмотрено далее на примере передачи тепла от узла t_x,y в температурном поле стыка крупных блоков наружной стены (рис. IV.7).


Применительно к произведенной разбивке расчетной сетки может быть выделен квадрат, в центре которого расположен рассматриваемый узел (на рисунке этот квадрат отмечен пунктиром). Этот квадрат обменивается теплом по направлениям к четырем соседним узлам сетки, температуры в которых равны t_x—Δ,y; t_x,y+Δ; t_x+Δ,y; t_x,y—Δ. Количества тепла, перетекающие по этим направлениям, будут зависеть от разности температур в соответствующих узлах и коэффициента теплопередачи (К/А) между этими узлами (обозначенных соответственно к_х—Δ; к_х+Δ; к_y+Δ; к_y—Δ.

В установившемся температурном поле, сумма количеств тепла, передаваемых от узла х, у к соседним узлам, должна быть равна нулю и из этого условия может быть получено наиболее общее выражение для t_x,y, а именно:


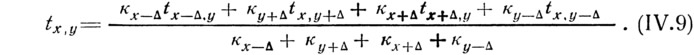
Если рассматриваемые смежные узлы расположены в пределах одного материала (λ=const), то все четыре коэффициента теплопередачи равны друг другу и выражение (IV.9) превращается в формулу (IV.8). При вычислении коэффициентов теплопередачи между узлами сетки перенос тепла принимается одномерным в пределах квадратов с размером сторон равным Δ, но центральных по отношению к линиям, соединяющим соответствующие узлы.

Так, например, от узла с температурой t_x,y к узлам с температурой t_x,y+Δ и t_x,y—Δ передача тепла происходит только в пределах квадратов abdc и cdef.

Коэффициент теплопередачи этих квадратов, т. е. величина обратная их термическому сопротивлению, определяется как средняя приведенная для элементов, состоящих из двух материалов, с учетом площадей каждого материала, по которым происходит теплообмен.



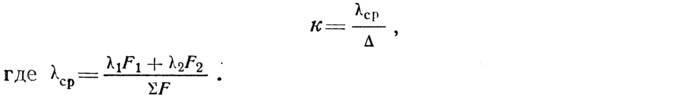
Теплообмен между узлом х, у и узлом х+Δ, у происходит в пределах квадрата hknm, а к узлу с температурой t_x—Δ,y в пределах квадрата ghml.

Коэффициенты теплопередачи этих квадратов вычисляются как для двухслойной стенки


Для квадратов из однородного материала к=λ/Δ. В этом случае, если расчетная сетка выбрана таким образом, что узел с температурой t_x,y лежит на поверхности конструкции, граничащей с воздушной средой (крайнюю первую нить расчетной сетки обычно совмещают с поверхностью конструкции, обращенной в помещение), коэффициент теплопередачи к воздуху принимается равным соответствующей величине коэффициента теплообмена (тепловосприятия α_в или теплоотдачи α_н), т. е. к=αF₁; R=1/αF₁.

При этом величины коэффициентов теплопередачи к соседним узлам, лежащим в этой плоскости, вводятся в расчет с коэффициентом 0,5, поскольку передача тепла по материалу происходит только по площади 0,5Δ, а по воздуху, в котором расположена вторая половина квадрата, теплообмен отсутствует.

Температурное поле, вычисленное для определенных значений температур внутреннего t_в и наружного воздуха t_н легко преобразовать для других значений этих температур, поскольку для любой точки n температурного поля


Описанный выше приближенный метод расчета плоского неоднородного температурного поля значительно облегчается при использовании счетно-решающих устройств (в частности, электроинтеграторов), сокращающих трудоемкую вычислительную работу.

Без применения этих устройств расчет температурного поля производился методом последовательного приближения (итерации). Во всех узлах расчетной сетки устанавливаются ориентировочные значения температуры, назначаемые по интуиции. Затем, пользуясь расчетными формулами (IV.8) или (IV.9), последовательно вычисляют значения температур во всех узлах, заменяя ими предыдущие до тех пор, пока эти значения в каждом узле сетки не будут удовлетворять соответствующим уравнениям.

Процесс расчета заканчивается, когда в пределах заданной точности значения температур становятся неизменяемыми во всех узлах сетки.

Число последовательных приближений, а следовательно, продолжительность и трудоемкость расчета зависят от того, насколько правильными были приняты начальные значения температур.

Моделирование температурных полей

Процессы переноса тепла путем теплопроводности и процессы электропроводности в материальных средах описываются дифференциальным уравнением одного и того же вида.

Для установившихся условий переноса в плоском поле это уравнение, как было указано в гл. I, имеет вид:


где Θ — потенциал переноса тепловой энергии (температура) или электроэнергии (электрический потенциал).

Полная аналогия потенциалов переноса определяет соответственную аналогию и для таких физических понятий, как тепловой поток и поток электричества, термическое сопротивление и омическое сопротивление. При этом преимуществом электростатического поля является то обстоятельство, что его параметры могут быть легко и быстро установлены измерительными приборами; аналогичные измерения для температурного поля обычно более затруднительны.

Полная аналогия между процессами переноса тепла и электричества и связанная с этим однотипность дифференциальных уравнений теплопроводности и электропроводности позволяет при расчете температурных полей пользоваться счетно-решающими устройствами типа электроинтегратора.

Электроинтегратор для моделирования плоских двумерных температурных полей представляет собой координатную сетку, между узлами которой могут быть подобраны и включены омические сопротивления, пропорциональные заранее вычисленным термическим сопротивлениям в рассматриваемом температурном поле. Координатная сетка накладывается на все изучаемое сечение ограждающей конструкции. Электроинтегратор присоединяется к сети постоянного тока. Крайние узлы сетки соединяются с токопроводящими шинами Ш₁ и Ш₂, имеющими разность потенциалов 0О, пропорциональную разности температур внутреннего и наружного воздуха, t_в—t_н.

Омические сопротивления между крайними узлами сетки и шинами подбираются пропорциональными сопротивлениям тепловосприятию и теплоотдаче.

На рис. IV.8 изображено моделирование температурного поля наружной стены с сквозным теплопроводным включением в виде прямоугольного элемента железобетонного каркаса.

Измерение величин электрических потенциалов в узлах сетки производится с помощью гальванометра Г, присоединенного к шине, и гибкого контакта, подключаемого к любому из узлов сетки. Гальванометр показывает разность потенциалов между шиной и соответствующим узлом сетки или непосредственно потенциал в узле.

Измеренные величины пропорциональны соответствующей разности температур или значению температур в рассматриваемом узле.

Замерив гальванометром или вычислив на основе замера разность потенциалов Θ_n между Ш₂ и узлом n, получим на основании пропорциональности температурных перепадов и разности электрических потенциалов:


откуда температура в произвольно выбранном узле n будет:


В узлах электрической модели температурного поля потенциалы, соответствующие искомым температурам, устанавливаются мгновенно после подбора надлежащих омических сопротивлений и включения электроинтегратора в сеть.

Время для проведения подготовленного эксперимента по вычислению температур в узлах плоского поля близко к продолжительности необходимых измерений гальванометром.

Трудоемких последовательных приближений не требуется. Счетно-решающие устройства типа электроинтегратора во много раз сокращают время для решения систему линейных уравнений, что необходимо при расчете температурных полей.

Примечания

1. Поскольку уравнение (1.8а) может быть справедливым для любого физического потенциала переноса энергии или вещества, а не только для температуры, являющейся потенциалом переноса тепла, формула (IV.8) правомерна и при расчете поля электрического потенциала и даже для изучения распределения давлений в капиллярно-пористой материальной среде.

В этих случаях значения температуры в уравнении (1.8а) заменяются соответственно величинами электрического потенциала или давления, а сопротивления проводимости тепла — соответствующими омическими или капиллярными сопротивлениями.