Эта аналогия не свободна от физических условностей, связанных с отмеченными выше коренными различиями в механизме переноса энергии и массы. Однако, если в дополнение к математическим обобщениям использовать установленные экспериментально константы переноса массы как внутри конструкции, так и на ее поверхностях, возможно изучение закономерностей переноса вещества на основе уравнений, аналогичных применяемым для описания процессов переноса энергии.
Если рассматривать перемещение влаги в капиллярно-пористых материальных средах с низким влагосодержанием, соответствующим воздушно-сухому состоянию материала, при котором перенос влаги в порах и капиллярах происходит преимущественно в парообразной фазе и в виде поверхностных пленок, за потенциал диффузии уместно принять парциальное давление водяного пара е (мм рт. ст.).
При этом в качестве константы диффузионного перемещения влаги принимается так называемый коэффициент паропроницаемости (μ г/м·ч·мм рт. ст.). При постоянной величине этого коэффициента математическая аналогия между нестационарной теплопроводностью и диффузией влаги через плоскую стенку, выполненную из капиллярно-пористого материала, может быть выражена следующим дифференциальным уравнением:
где e — парциальное давление водяного пара, мм рт. ст.; τ — время, ч или сут; μ — коэффициент паропроницаемости материала, г/м·ч·мм рт. ст.; ξ — удельная влагоемкость материала, г/кг·мм рт. ст. (при изменении влагосодержания в пределах сорбционного увлажнения); γ — объемный вес материала, кг/м3.
Методы определения коэффициента паропроницаемости и влагоемкости для целей расчета изменений влажностного состояния конструкций рассмотрены в гл. VI. Поскольку влагоемкость материала зависит от изменений температуры и с последними связана также и величина насыщающего парциального давления водяного пара в материальной среде, удельная влагоемкость ξ заменяется относительной ξ0 (см. статью), связанной с ней зависимостью:
где Et — максимальное парциальное давление, соответствующее насыщенному состоянию (100%-ной гигроскопической влажности) материала при рассматриваемой температуре. Тогда уравнение (1.28) примет вид:
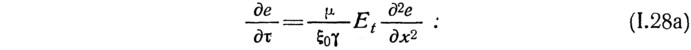
Таким образом, влияние изменений температуры учитывается введением в уравнение величины Et.
При численном решении уравнения (1.28а) обычно пользуются методом конечных разностей.
Применение этого уравнения для целей расчета изменений влажностного состояния ограждающих конструкций предложено К. Ф. Фокиным и практические методы расчета этих изменений разработаны им же.
При рассмотрении изменений влажностного состояния конструкций с более высоким влагосодержанием в воздушной среде с постоянной неизменной температурой, за потенциал переноса влаги может быть принято влагосодержание материала со (кг/кг).
Ранее было приведено уравнение влагопроводности (при одномерном переносе влаги) внутри конструкции, аналогичное уравнению Фурье для неустановившегося переноса тепла путем теплопроводности. В этом уравнении
перемещение влаги однозначно определяется градиентом влагосодержания, что может быть справедливым только в изотермических условиях, т. е. когда grad t=0.
Эти ограничения достаточно соответствуют, например, условиям естественной сушки конструкции с повышенным влагосодержанием в теплое время года, когда среднесуточные значения температур помещения и наружного воздуха почти не отличаются друг от друга.
Использование в этих целях уравнения влагопроводности для приближенных сравнительных расчетов сроков естественной сушки конструкций стен приведено в гл. VI. При этом в таких расчетах имеется существенное допущение, состоящее в том, что показатели перемещений влаги в капиллярно-пористом материале принимаются за постоянную величину.
В действительности интенсивность перемещений влаги уменьшается по мере уменьшения влагосодержания материала, и это допущение может быть оправдано только в том случае, если для целей расчета будет принято среднее значение константы перемещений влаги за весь период естественной сушки конструкции, а также осредненные условия влагообмена на ее поверхностях.
Множитель пропорциональности
перед правой частью уравнения может быть назван коэффициентом нестационарной влагопроводности и по своей структуре и физической размерности м2/ч или см2/сут аналогичен коэффициенту температуропроводности в уравнении Фурье. Здесь величина x, г/м·ч%, представляет коэффициент влагопроводности в установившихся условиях, являющийся аналогом коэффициента теплопроводности; ξ — выражает удельное водопоглощение капиллярно-пористого материала, г/кг%; а γ, кг/м3 — его объемный вес.
Если изотермических условий для рассматриваемой конструкции не существует и она подвергается воздействию перепада температур, закономерности перемещения влаги могут быть осложнены явлениями термодиффузии, связанными с переносом массы вещества от участков с более высокой температурой к участкам с более низкой температурой.
В основе этого явления лежит разность температур и связанное с ней различие поверхностных натяжений и адсорбционных сил пленочной влаги, перемещающейся по поверхности капилляров пористого материала1 под влиянием этой разности.
Экспериментальные исследования перемещений влаги в ограждающих конструкциях зданий показывают, что явления термодиффузии могут иметь значительное количественное выражение и практическую значимость главным образом при сверхгигроскопическом влагосодержании капиллярно-пористой материальной среды и резко выявленном градиенте температуры.
Такие параметры температурно-влажностного состояния не всегда характерны для условий эксплуатации ограждающих конструкций зданий, где влагосодержание сравнительно невелико, а перепады температур ограничены.
Математическое выражение условий переноса влаги при явлениях термодиффузии существенно усложняется, поскольку механизм переноса теряет однозначность, и влагосодержание материала уже не может являться потенциалом переноса, что было характерным для уравнения влагопроводности.
Дифференциальное уравнение переноса влаги в материальной среде (при одномерном перемещении в направлении х) имеет вид:
где θ — потенциал переноса, являющийся функцией влагосодержания материала и внешних параметров среды; размерность потенциала может быть установлена в градусах специальной шкалы°В; τ — время; am=x/ξγ — коэффициент нестационарной влагопроводности; δ(°B/°C) — коэффициент термовлагопроводности, отнесенный к разности потенциалов переноса влаги.
Первый член правой части уравнения выражает процесс влагопроводности в изотермической материальной среде; второй член — процесс переноса влаги, вызванный градиентом температуры.
При отсутствии перепада температур, второй член становится равным нулю и уравнение (1.29) превращается в уравнение влагопроводности, в котором обобщенный потенциал переноса может быть заменен влагосодержанием материала.
При градиенте температуры, значимость термодиффузионного переноса зависит от величины градиента, а также от свойств и влагосодержания материала; поскольку из уравнения
следует, что
выражение для переноса влаги термодиффузией может быть представлено, как
где а — коэффициент температуропроводности материала, м2/ч; Lu — критерий Лыкова, представляющий отношение интенсивностей переноса влаги и тепла.
Таким образом, значимость переноса влаги термодиффузией зависит от критерия Lu и изменений (колебаний) температуры во времени.
При малом влагосодержании внешних частей ограждающей конструкции (когда am→min и Lu приближается к нулю) резко выраженные колебания температуры во времени являются возможным путем активизации естественной сушки2.
Если рассматривать изменения влажностного состояния конструкций в пределах невысокой влажности, соответствующей воздушно-сухому состоянию конструктивных слоев, граничащих с воздушной средой, и производить такое рассмотрение при среднемесячных значениях температуры, полагая суточные ее колебания заведомо небольшими, влияние термодиффузии окажется очень малым. В этом случае уравнение (1.29) принимает вид диффузионного уравнения Фурье:
Если основной причиной изменений влажностного состояния воздушно-сухой конструкции является диффузия водяного пара, за потенциал переноса влаги принимается парциальное давление, а величина аm становится прямо пропорциональной коэффициенту паропроницаемости μ. Уравнение (1.31) записывается в виде (1.28).
Таким образом, в основу разработки инженерных методов расчета естественной сушки конструкций в изотермической воздушной среде и расчета сезонных изменений влажностного состояния воздушно-сухих конструкций могут быть положены однотипные дифференциальные уравнения.
Примечания
1. Точнее — по слоям молекул влаги, адсорбированным на этой поверхности.
2. В связи с этим, естественная сушка ограждающих конструкций наиболее эффективна в районах с континентальным климатом и интенсивной солнечной радиацией. Уровень среднесуточной температуры тоже важен, но имеет подчиненное значение.
