Расчет теплопроводных включений в ограждающих конструкциях

Местные понижения температуры на обращенной в помещение поверхности неоднородной ограждающей конструкции, имеющей конструктивные включения из материалов с относительно большей теплопроводностью, чем основная масса материала, могут привести к образованию конденсата. Такими теплопроводными включениями являются элементы бетонного, железобетонного или стального каркасов; в железобетонных слоистых панелях — неутепленные обрамления и контурные ребра жесткости; в утепленных, пустотных и засыпных каменных конструкциях — связующие ряды кладки (например, прокладные ряды), включения плотного материала между пустотами или отдельными участками утепления, сквозные швы тяжелых растворов, применяемых при укладке камней или плит из малотеплопроводных материалов.

В общем случае распределение температур в одной из проекций (чаще всего в плане) конструкции с теплопроводными включениями может быть установлено кратко описанным выше построением плоского температурного поля на основе численного решения дифференциального уравнения Лапласа. Однако для теплопроводных включений простейшей формы (см. схемы в табл. IV.2), пересекающих всю толщину ограждающей конструкции или половину ее, существуют приближенные инженерные расчеты, позволяющие судить о достаточности теплозащитных свойств конструкции.


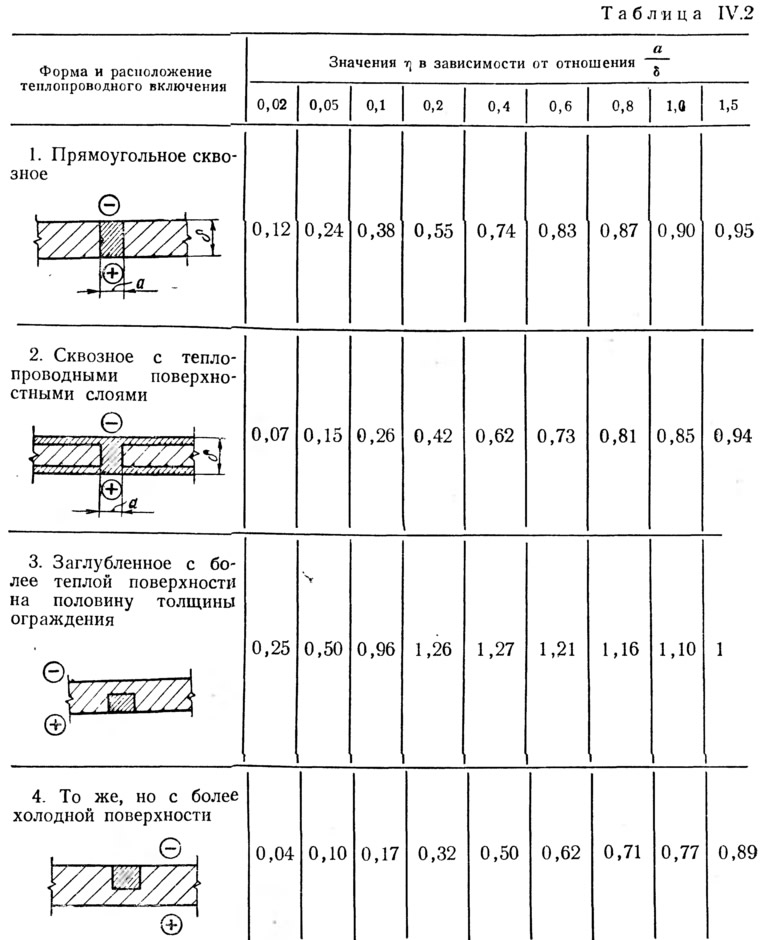
Основой для разработки таких инженерных методов расчета послужили многочисленные построения двумерных температурных полей ограждающих конструкций, пересекаемых элементами железобетонного каркаса. Обобщение результатов этих построений было выполнено следующим образом.

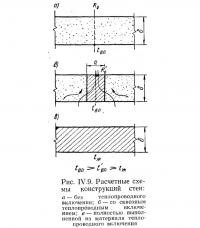
Если рассмотреть значения температур на поверхности стены: а) по сечению конструкции вдали от теплопроводного включения, t_в.п и б) по теплопроводному включению, t'_в.п; в) полностью выполненной из материала теплопроводного включения, — t_ж, то будет очевидно, что (рис. IV.9)


Результаты построений температурных полей показали, что значение t'_в.п зависит главным образом от соотношения ширины включения к толщине стены a/δ чем меньше это соотношение, тем выше t'_в.п и ближе к значению t_в.п. В пределе, при а=0, t'_в.п=t_в.п. Наоборот, чем больше соотношение a/δ, тем ниже t'_в.п и ближе к значению t_ж. При достаточно большом соотношении a/δ>2; t'_в.п=t_ж.

Можно полагать, что разность температур поверхности стены и поверхности включения t_в.п—t'_в.п составляет некоторую часть от разности t_в.п—t_ж, т. е.


где η — коэффициент, представляющий собой безразмерное соотношение разностей температур


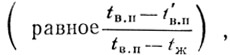
характеризующее интенсивность перетекания тепла к теплопроводному включению и зависящее от его геометрической формы, расположения в стене и соотношения а/δ.

Значения коэффициента η для наиболее характерных видов теплопроводных включений принимаются по табл. IV.2.

Из выражения для температуры на поверхности конструкций (1.24а), получим:


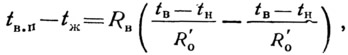
где R_o и R'_o — сопротивления теплопередаче конструкции и теплопроводного включения.

Подставив полученное выражение в уравнение (а), после преобразования, получим:


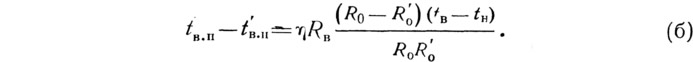
Замечая, что поток тепла Q, проходящий через ограждающую конструкцию при отсутствии в ней теплопроводных включений, может быть представлен выражением Q=(t_в—t_н)/R_o, а произведение R_вQ — выражено разностью температур и подставляя эти выражения в (б), получим:


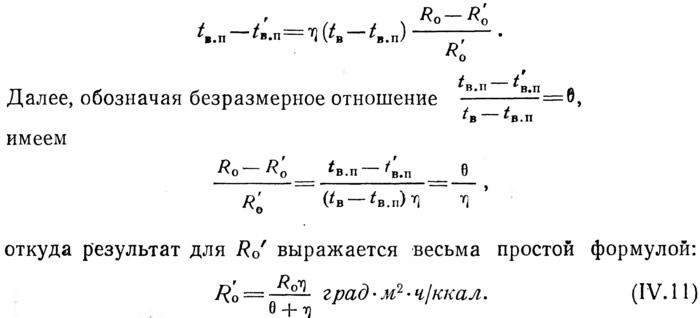
Введение безразмерного симплекса θ, характеризующего надежность проектируемой конструкции против появления конденсата на наиболее опасном участке поверхности, позволяет упростить расчетное выражение.

Формула (IV.11) дает возможность вычислить необходимое сопротивление теплопередаче проектируемой ограждающей конструкции в месте расположения теплопроводного включения, если предельно допустимое значение температуры t'_в.п на внутренней поверхности включения принять равным температуре точки росы t_росы.

Безразмерная величина θ, входящая в формулу (IV.11), зависит от температуры t_в и влажности воздуха φ_в в помещении, а также от степени утепленности конструкции. Такая степень может быть выражена отношением принятого при проектировании сопротивления теплопередаче к его требуемой величине


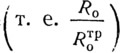
Иначе говоря

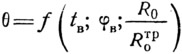
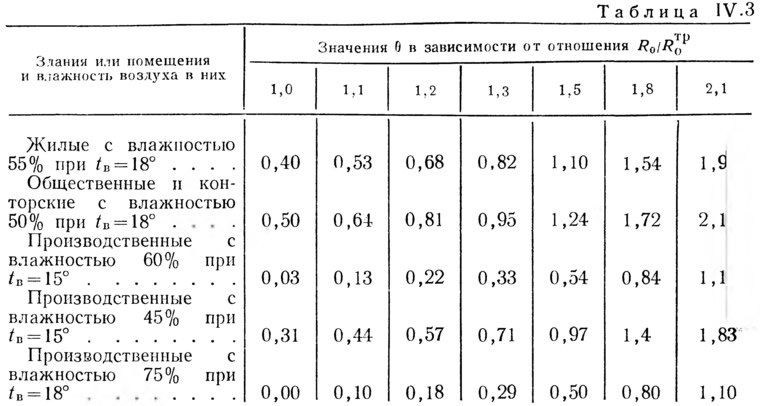
Значения величины θ для ограждений в помещениях различного назначения указаны в табл. IV.3.


Выражение для вычисления температуры на внутренней поверхности теплопроводных включений может быть приведено к наглядному и удобному для пользования виду путем преобразования формулы (IV.11).

Обозначив R_o/R'_o = получим:


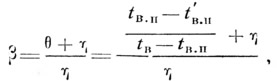
откуда, определяя t'_в.п, найдем:


Из этого выражения можно видеть, что понижение температуры на поверхности теплопроводного включения по сравнению с температурой на поверхности нормально утепленных участков ограждения, зависит от геометрических размеров, формы и расположения включения (характеризуемых величиной η), а также от степени утепленности конструкции (оцениваемой величинами β и t_в—t_в.п).

Результаты, получаемые по формуле IV. 12, полностью совпадают с данными расчета по более сложной формуле IV.13, устанавливающей зависимость температуры внутренней поверхности ограждения в местах теплопроводных включений от температуры воздуха помещения t_в [3]:


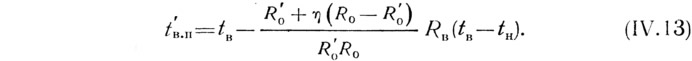
Поскольку наименьшие величины ц соответствуют включениям с теплопроводными слоями на поверхностях конструкции и особенно включениям, расположенным в более холодной наружной части ограждения, понижение температур на поверхности конструкции, обращенной в помещение, будет при наличии включений указанных видов наименьшим. Температуры распределяются более равномерно, поскольку тепло, распространяющееся вдоль поверхности конструкции, обращенной в помещение, способствует выравниванию их значений. Однако протяженность зоны искажений температурного поля (из-за наличия включения) возрастает. Наоборот, понижение температуры будет более значительным и резким (хотя и распространяющимся на меньшую длину ограждения) при сквозных включениях прямоугольной формы и включениях, расположенных с более теплой поверхности конструкции².

Необходимое сопротивление теплопередаче R'_o по теплопроводному включению зависит от формы и расположения включения (что характеризуется величиной ц и температурно-влажностной характеристикой помещения, выражаемой значением θ).

Из выражения IV.11 видно, что при θ=0 и любых возможных (в пределах от 0 до 1) значениях η, R'_o=R_o; это означает, что для конструкций, ограждающих влажные помещения и имеющих ограниченные минимальными требованиями норм теплозащитные свойства, наличие теплопроводных включений любой геометрической формы и размера недопустимо. Возможность появления теплопроводных включений в ограждениях влажных помещений появляется лишь для конструкций с сопротивлением теплопередаче, значительно превышающим нормируемые значения.

По мере уменьшения влажности воздуха в ограждаемых помещениях и увеличения степени утепленности конструкций, возрастает возможность применения ограждении с теплопроводными включениями.

В частности, применение изделий из легких бетонов с малой теплопроводностью, но стандартными размерами может обеспечить высокую утепленность наружных стен сухих производственных помещений и позволяет использовать ограждающие конструкции со сквозными элементами каркаса ограниченной ширины.

Пример IV.2. Пенобетонные блоки толщиной 0,25 м применены для заполнения каркасной стены производственного помещения с сухим режимом.

Расчетная температура наружного воздуха равна —30°, внутреннего воздуха +15°. Расчетная относительная влажность 45%. Сечение элемента бетонного каркаса 0,25·0,15 м.

Требуется определить, можно ли вести заполнение блоками в одной плоскости с каркасом с тем, чтобы элементы последнего пересекали всю толщину стены (рис. IV.10).


Здесь 0,22 — коэффициент теплопроводности пенобетона при объемном весе 800 кг/м³ и сухих условиях эксплуатации.

Это сопротивление теплопередаче превышает нормируемую величину 0,62 град·м²·ч/ккал примерно в 2,1 раза


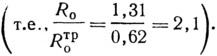
При этой величине отношения R_o/R^тр_o величина 0 равна 1,83 (табл. IV.3) и необходимое сопротивление теплопередаче конструкции по теплопроводному включению:


Фактическое сопротивление теплопередаче элемента бетонного каркаса (бетон с кирпичным щебнем в сухих условиях эксплуатации λ=0,80 ккал/м·ч·град):


что практически равно необходимому.

---

Таким образом, при высоких теплозащитных свойствах стен сухих помещений сквозные элементы бетонного каркаса с ограниченным поперечным сечением не всегда являются причиной появления конденсата на внутренней поверхности стены³.

В отапливаемых зданиях с более теплопроводными элементами каркаса из железобетона или стали необходимо располагать такие элементы у внутренней поверхности стен, не заглубляя их в конструкцию даже в сухих помещениях.

При облегченных ограждающих конструкциях, малая толщина которых достигается за счет применения эффективных утеплителей, расположение ограждения с внешней стороны каркаса является обязательным правилом.

Теплопроводные включения в стенах из легкобетонных камней или блоков могут быть образованы за счет большей теплопроводности строительного раствора, примененного для заполнения швов.

Теплофизический расчет сопряжений между блоками и камнями с заполнением стыков тяжелым раствором может быть выполнен при использовании выражения (IV.11).

Пример IV.3. Для жилых домов в местности с расчетной температурой наружного воздуха t_н=—34°, проектируется применение стен толщиной δ=0,25 м из блоков ячеистого бетона. Требуется установить, можно ли вести кладку на цементно-песчаном растворе, если толщина швов а=0,015 м. Отношение


Сопротивление стены теплопередаче:


где 0,60; 0,25; 0,75 — коэффициенты теплопроводности внутренней фактуры, ячеистого бетона с объемным весом 800 кг/м³ и наружной фактуры.

Нормируемое сопротивление стены теплопередаче R^тр_o=1,16 град·м²·ч/ккал. Сопротивление теплопередаче стены по шву (при λ цементно-песчаного раствора равном 0,80):


тогда как по IV.11 требуется:


Здесь величина θ=0,49 определена интерполяцией по табл. IV.3 для


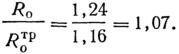
Разница между необходимым и имеющимся сопротивлениями теплопередаче по шву незначительна (0,49—0,44=0,05) и появление конденсата на внутренней поверхности швов в большой мере будет зависеть от колебаний влажности воздуха в помещении, а также от степени увлажнения цементного камня в шве и от действительной величины его коэффициента теплопроводности. При уменьшении коэффициента теплопроводности цементно-песчаного раствора, например, до 0,65 ккал/м·ч·град, что соответствует сухому состоянию мелкопористого цементного камня, вероятность конденсации в местах расположения швов полностью устраняется, даже при кратковременных повышениях влажности воздуха в помещении.

Вероятность конденсации влаги на внутренней поверхности стен из легкобетонных камней и блоков в местах расположения швов особенно велика во влажных климатических районах, где раствор, заполняющий шов, может быть увлажнен атмосферной влагой. В этом случае выполнение швов с пустотой внутри препятствует капиллярным перемещениям влаги по всей толщине стены, обеспечивает быстрое высыхание затвердевшего раствора после возможных эпизодических увлажнений и одновременно увеличивает сопротивление теплопередаче конструкции в месте шва.

Таким конструктивным приемом при возведении стен предотвращается также возможное промерзание швов, что в особенности важно для суровых климатических районов с повышенной влажностью.

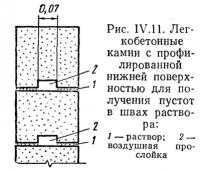
Внутренние пустоты в швах могут быть образованы при помощи стальной или деревянной рейки-шаблона, укладываемой на поверхность камня при нанесении раствора, а также при использовании легкобетонных камней с профилированной нижней поверхностью, получаемой при изготовлении (рис. IV.11).

Стена из ячеистобетонных камней, рассмотренная в предыдущем примере, полностью удовлетворяет теплофизическим требованиям даже при повышении влажности помещения до 60% в том случае, если швы будут выполнены пустотными. В самом деле, сопротивление теплопередаче пустотного шва


где 0,20 — термическое сопротивление воздушной прослойки по табл. I—8. Эта величина сопротивления теплопередаче пустотного шва превышает требуемое значение при влажности φ=60%:


В действительности сопротивление теплопередаче пустотного шва будет еще выше за счет сухого состояния и меньшего значения коэффициента теплопроводности цементного камня.

Пользуясь формулой IV.12, легко вычислить значения температуры на поверхности теплопроводных включений, обращенной в помещение.

Пример IV.4. Вычислить температуру на внутренней поверхности стены из пенобетонных блоков (см. пример IV.2) и на поверхности бетонного каркаса, пересекающего эту стену, при расчетной температуре наружного воздуха —30°.

Сопротивление теплопередаче стены из пенобетонных блоков R_o=1,50 град·м²·ч/ккал, а элемента бетонного каркаса R'_o=0,49 град·м²·ч/ккал.

Температуру на внутренней поверхности стены вычисляем по формуле (1.24, а):


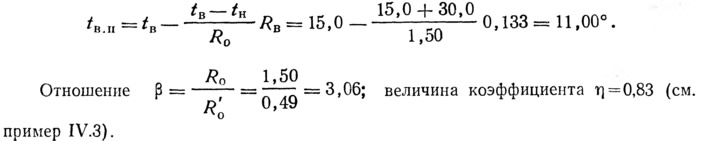
Температура на внутренней поверхности бетонного каркаса, пересекающего заполнение стены (IV.12):


Такой же результат может быть получен расчетом по формуле (IV.13).

---

Приведенные выше приближенные способы теплофизических расчетов теплопроводных включений относятся к однородным ограждающим конструкциям с теплопроводными включениями простейшей геометрической формы и при этом расположенными на значительном удалении друг от друга, что исключает влияние соседних включений на процессы перетекания тепла.

Для других видов ограждающих конструкций и более сложной формы или более близкого расположения теплопроводных включений, что часто встречается в практике проектирования, простых расчетных формул не существует.

Исключение представляет инженерный метод расчета температуры на поверхности вертикальных стыков трехслойных панелей, предложенный Ф. В. Ушковым на основе исследования большого количества температурных полей подобных стыков.

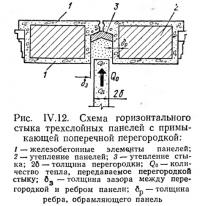
Обычно к вертикальному стыку панелей жилых зданий примыкает поперечная перегородка, влияющая на распределение температур (рис. IV.12), поскольку по перегородке передается в зону стыка некоторое количество тепла, пропорциональное эквивалентному коэффициенту теплопередачи перегородки, равному:


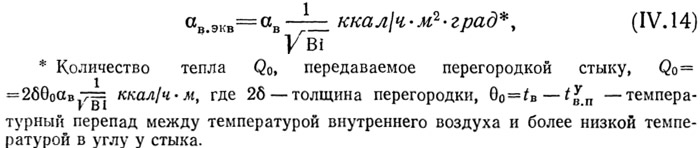
где α_в — коэффициент теплообмена на внутренней поверхности перегородки; Bi — критерий Био для перегородки, характеризующий отношение тепла, поступающего из помещения через ее поверхность, к количеству тепла, распространяющемуся внутри конструкции, а именно:


где λ — коэффициент теплопроводности материала перегородки, ккал/м·ч·град; δ — характерный размер перегородки, равный половине ее толщины, м.

Делением эквивалентного коэффициента теплоотдачи перегородки на коэффициент теплообмена ее внутренней поверхности, получают относительный коэффициент интенсификации теплообмена α_отн между перегородкой и стыком (иначе называемый коэффициентом оребрения):


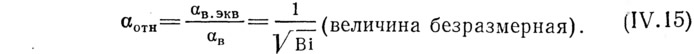
Для расчета температуры в углу стыка (рис. IV.12) необходимо предварительно вычислить приведенное сопротивление теплопередаче стыка, определяемое по формуле:


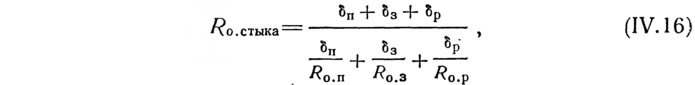
где δ_п — половина толщины перегородки; δ_з — толщина зазора между перегородкой и ребром панели; δ_р — толщина обрамляющего ребра; R_о.п; R_о.з; R_о.р — сопротивления теплопередаче панели в сечениях по оси перегородки, зазору и обрамляющему ребру. При вычислении R_о.п термическое сопротивление перегородки и сопротивление тепловосприятию принимаются: R_в.п=1/(α_вα_отн). После этих предварительных вычислений, для приближенного расчета минимальной температуры в углу стыка t^у_в.п можно пользоваться формулой:


Результат, получаемый по этой приближенной формуле, обычно отклоняется не более чем на 1° от значений температуры в углу, установленных точным расчетом двумерного температурного поля.

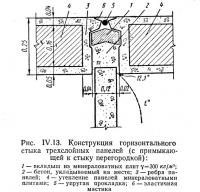
Пример IV.5. Определить наинизшую температуру в углу стыка трехслойных панелей и примыкающей к стыку перегородки. Наружная температура —30°, внутренняя +18°. Общая толщина панелей 0,25 м; утепление минераловатными плитами; перегородка бетонная, толщиной 0,12 м (рис. IV.13). Термовкладыш в стыке толщиной 0,04 м из минераловатных плит. Характерный размер (половина толщины) перегородки δ_п=0,06 м; ширина зазора δ_з=0,02 м; толщина ребра δ_р=0,04 м.

Примечания

1. В числителе разность температур на поверхности конструкции и поверхности теплопроводного включения заданной ширины, а в знаменателе — разность температур на поверхностях конструкции и бесконечно протяженного теплопроводного включения.

2. Такие особенности распределения температур в зоне теплопроводных включений различного вида подтверждаются опытом эксплуатации зданий с соответствующими конструктивными решениями панельных стен. Если ребра в стыках панелей покрыты с теплой стороны теплопроводным защитно-отделочным слоем, распределение температур на внутренней поверхности стены более равномерно; при отсутствии достаточно толстого и теплопроводного слоя отмечается явно выраженное понижение температуры вблизи стыка.

3. Это подтверждается практикой эксплуатации термических, кузнечных и других сухих и хорошо вентилируемых цехов. Однако и в таких цехах следует избегать расположения элементов каркаса вблизи наружных углов, где величина коэффициентов тепловосприятия α_в меньше чем на поверхности плоских участков стены, что связано с возможностью понижения температуры в зоне углов.

Сквозное пересечение стен указанных выше помещений элементами каркаса возможно преимущественно в том случае, если эти элементы выполнены из бетона с небольшой теплопроводностью (с легкими заполнителями и небольшим процентом армирования) и имеют небольшое поперечное сечение.