Для многих современных конструкций недопустимо принимать для теплофизического расчета конструктивную схему, относящуюся к преобладающей и наиболее благополучной части ограждения, оставляя без внимания его пониженные теплозащитные свойства на других участках, например, в местах конструктивных ребер, стыков и сопряжений.
На таких отдельных участках поперечное сечение ограждающей конструкции часто состоит из других более теплопроводных материалов и обладает меньшим сопротивлением теплопередаче.
В этих случаях задачей теплофизического расчета является: а) определение средней приведенной величины сопротивления теплопередаче: именно эта величина должна превышать требуемое нормами сопротивление; б) определение необходимых теплозащитных свойств наименее утепленных участков конструкции в целях обеспечения температур выше точки росы на их поверхности и исключения образования конденсата.
Теплофизический расчет неоднородных ограждающих конструкций совершенно необходим для многих современных конструкций, выполняемых из крупных элементов (панельных, щитовых и т. д.).
Определение сопротивления теплопередаче таких конструкций по оптимальному характерному сечению дает завышенные результаты, существенно отличающиеся от действительных значений, получаемых при рассмотрении неоднородной ограждающей конструкции в целом.
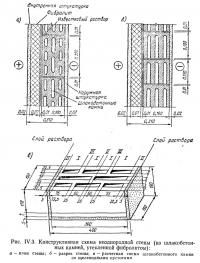
При расчете общего сопротивления теплопередаче неоднородных конструкций различают два случая. Первый, более простой случай, относится к конструкциям, которые на отдельных (сравнительно небольших по площади) участках пересекаются по всей толщине конструктивными элементами с несколько большей теплопроводностью, чем преобладающая часть конструкции.
Таковы, например, стены с прокладными рядами, заполнение железобетонного каркаса или фахверка, панельные конструкции с обрамлениями или ребрами по контуру панели и т. д. (рис. IV.2).
-В этом случае по поверхности ограждающей конструкции определяется площадь, занимаемая каждым характерным конструктивным элементом (FI, FII и т. д.), и по формулам (1.22) и (1.22а) вычисляется термическое сопротивление каждого такого конструктивного элемента (RI, RII и т. д.). После этого среднее приведенное значение термического сопротивления неоднородного ограждения в целом вычисляется по приближенной формуле:
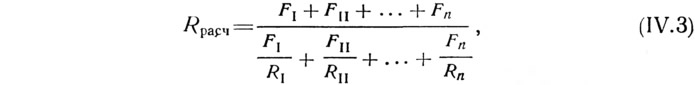
а общее сопротивление теплопередаче — по формуле (1.23). Второй, более сложный случай, относится к конструкциям неоднородным в двух измерениях (например, стены из пустотелых камней и т. д.).
Теплофизический расчет таких ограждающих конструкций производится последовательно двумя различными приемами: а) путем вычисления среднего приведенного термического сопротивления при мысленной разрезке конструкции на отдельные характерные участки плоскостями, параллельными основному направлению потока тепла; при этом термические сопротивления отдельных участков находятся по формуле (1.22а), т. е.:
а среднее приведенное значение R|| термического сопротивления для конструкции в целом определяется по формуле (IV.3); б) путем вычисления среднего приведенного термического сопротивления при мысленной разрезке конструкции плоскостями, перпендикулярными основному направлению потока тепла, на отдельные характерные слои, которые могут состоять или из одного материала, или из нескольких. Для слоев, состоящих из нескольких материалов, вычисляется средний приведенный коэффициент теплопроводности по формуле:
где λ1, λ2, ..., λn — коэффициенты теплопроводности материалов; F1, F2, ..., Fn — площади, занимаемые в конструкции или характерном ее участке этими материалами (их выражают в процентах, принимая общую сумму площадей за 100%).
Термическое сопротивление однородных слоев определяется при этом виде разрезки по обычной формуле (1.22), а термическое сопротивление конструкции в целом R⊥ получается суммированием сопротивлений отдельных слоев.
Для ограждающих конструкций, у которых величины R|| и R⊥ отличаются друг от друга не более, чем на 25—40%, расчетное значение термического сопротивления Rрасч может быть вычислено по приближенной формуле:
В тех случаях, когда ограждающая конструкция состоит из одинаковых повторяющихся изделий (например, пустотных камней), целесообразно вычислить средние приведенные термические сопротивления этих изделий, после чего теплофизический расчет сопротивления теплопередаче может быть произведен как для обычной слоистой конструкции.
Пример IV.1. Определить сопротивление теплопередаче стены толщиной 0,19 м из шлакобетонных камней со щелевидными пустотами, утепленной с внутренней поверхности плитами из фибролита толщиной 0,07 м и покрытой наружной и внутренней штукатуркой (рис. IV.3). Стена проектируется для помещений с нормальной влажностью и умеренного наружного климата.
Приняты коэффициенты теплопроводности: 1) шлакобетона с объемным весом 1600 кг/м3 λ1=0,65 ккал/м·ч·град; 2) раствора известково-песчаного 1550 кг/м3 λ2=0,65 ккал/м·ч·град; 3) фибролита с объемным весом 350 кг/м3 λ3=0,14 ккал/м·ч·град; 4) известковой внутренней штукатурки с объемным весом 1600 кг/м3 λ4=0,60 ккал/м·ч·град; 5) наружной штукатурки с объемным весом 1700 кг/м3 λ3=0,75 ккал/м·ч·град.
Расчетная схема камня со щелевидными пустотами с разбивкой на отдельные характерные участки и слои изображения на рис. IV.3, в. Определяем среднюю приведенную величину термического сопротивления камня.
А. Расчет при разрезке плоскостями, параллельными потоку тепла.
Участок I. Наружные и внутренние шлакобетонные стенки камня и три щелевидных пустоты со средним термическим сопротивлением 0,20 град м2·ч/ккал каждая.
Общая площадь участка I, через которую проходит поток тепла:
Термическое сопротивление
Участок II. Наружные шлакобетонные поперечные стенки камня и вертикальные швы раствора:
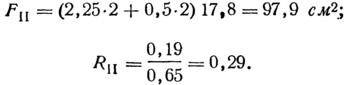
Участок III. Наружные и внутренние шлакобетонные стенки камня и одна центральная щелевидная пустота:
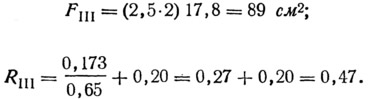
Участок IV. Наружные и внутренние шлакобетонные стенки по оси симметрии камня и две щелевидных пустоты:
Участок V. Горизонтальная шлакобетонная диафрагма камня и раствор горизонтального шва:
Сумма площадей характерных участков ∑F=480,6+97,9+89+44,5+88=800 см2, т. е. равна общей боковой вертикальной поверхности камня, уложенного на растворе в стену, 40·20=800 см2.
Термическое сопротивление пустотного камня, уложенного в стену, по расчету при разрезке конструкции плоскостями, параллельными потоку тепла:
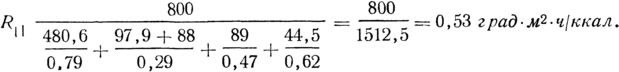
Б. Расчет при разрезке плоскостями, перпендикулярными потоку тепла
Слой 1. Продольные шлакобетонные стенки камня с учетом швов раствора и горизонтальной диафрагмы.
Площадь шлакобетона, через которую проходит поток тепла: F1, ш=39·19=741 см2; площадь раствора: F1, р=19+40=59 см2. Полная площадь F1=800 см2. Термическое сопротивление
Слои — 2 и 3. Щелевидные пустоты камня с учетом разъединяющих их шлакобетонных стенок, а также швов раствора и горизонтальной диафрагмы.
1) Приведенная площадь воздушных прослоек:
2) Площадь шлакобетона и раствора:
Термическое сопротивление воздушных прослоек Rв.п=0,20·3=0,60; шлакобетона Rш=0,067/0,065=0,10.
Среднее значение термического сопротивления:
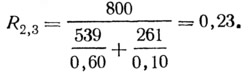
В целом термическое сопротивление пустотного камня, уложенного в стену, по расчету при разрезке конструкции плоскостями, перпендикулярными потоку тепла: R⊥=0,19+0,23=0,42 град·м2·ч/ккал.
Расчетное значение термического сопротивления шлакобетонного камня в стене, полученное по формуле (IV.5), на основании приведенных выше двух приемов расчета:
Тогда среднее расчетное значение коэффициента теплопроводности шлакобетонного камня со щелевидными пустотами и глухой горизонтальной диафрагмой:
Общее сопротивление теплопередаче всей слоистой конструкции в целом:
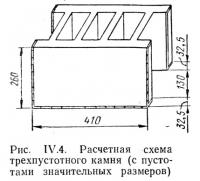
Аналогичный расчет шлакобетонного трехпустотного камня с пустбтами значительных размеров (рис. IV.4) показывает, что расчетное значение коэффициента теплопроводности, практически равное полученному выше значению для камня со щелевидными пустотами (λср=0,42 ккал/м·ч·град), может быть получено только при заполнении шлаком трех крупных пустот каждого камня.
Слоистая конструкция стены с камнями, засыпанными шлаком, более трудоемка, а потому применение камней со щелевидными пустотами, не нуждающимися в засыпке, более предпочтительно.