При определенных теплофизических свойствах рассматриваемой конструкции или материальной среды и установившейся (т. е. не изменяющейся во времени) разности температур, вызывающей процесс теплопередачи, значение температуры в любой произвольной точке конструкции является функцией только координат пространства, т. е. t=f(x, у, z)1. При изменяющихся во времени внешних условиях, вызывающих процесс теплопередачи, температура в произвольной точке зависит не только от координат пространства, но и от времени t=f(x, у, z, τ)2.
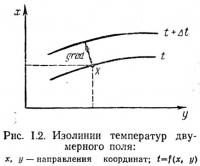
В строительной теплофизике пространственные температурные поля рассматриваются сравнительно редко, поскольку для практических целей в большинстве случаев достаточно изучить двумерное температурное поле, возникающее в одной из проекций, т. е. в плане или разрезе конструкций. В этом случае, при установившихся условиях теплопередачи, температура в каждой точке проекции конструкции является функцией двух координат: t=f(x, у).
Третья координата (т. е. высота или длина конструкции) предполагается достаточно протяженной, а потому не влияющей на распределение температур в плоском сечении.
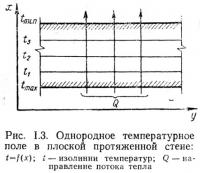
Закономерность изменений температурного поля наиболее наглядно можно представить, нанеся линии равных температур (изотермы) в изучаемой проекции конструкции. Наиболее резкое изменение температуры отмечается по нормали к изолиниям (рис. 1.2). Эта нормаль совпадает с направлением температурного градиента (повышения температур) между изолиниями и противоположна (обратна на 180°) наиболее вероятному направлению теплового потока Q, переносящего тепло от более высокой температуры к более низкой. В однородной плоской бесконечно протяженной стене с постоянной разностью температур на противоположных поверхностях эти изолинии параллельны друг другу и поверхностям ограждения; направление потока тепла возможно для этой конструкции только в одном направлении (рис. 1.3), а функциональная зависимость изменений температуры наиболее проста: t=f(x). Это случай наиболее элементарного одномерного температурного поля в установившихся (стационарных) условиях теплопередачи.
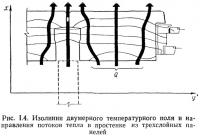
Изолинии температур в конструкциях с более сложной геометрической формой выражаются двумерным температурным полем и обычно не параллельны поверхностям ограждения, а криволинейны. При криволинейном очертании изотерм пути распространения тепла Q (нормальные к изотермам) также не могут быть параллельными друг другу, как это видно из рис. 1.4, на котором показано двумерное температурное поле простенка наружной стены, выполненного из трехслойных панелей.
При установившихся условиях теплопередачи внешние тепловые воздействия (значения и разность температур) постоянны (или принимаются таковыми в целях упрощения расчетов процессов передачи тепла, которые без особых погрешностей можно свести к установившимся условиям).
В действительных условиях внешние тепловые воздействия (например, наружные температуры) изменяются во времени, что приводит к нестационарной теплопередаче и изменчивости температурного поля.
В теплофизических расчетах ограждающих конструкций зданий важное значение имеет рассмотрение температурного поля этих конструкций при периодических изменениях внешних воздействий (например, периодическое охлаждение или прогрев, вызванные циклическим режимом производства, периодической теплоотдачей отопительных систем, ежедневным облучением солнцем и т. д.). Та-кое нестационарное температурное поле, для которого характерны закономерные периодические изменения, называют квазистационарным.
Рассмотрение квазистационарного температурного ,поля позволяет найти расчетные методы, более конкретные и удобные для практики, чем общие методы расчета нестационарного поля. Объясняется это тем, что при квазистационарном теплообмене, кроме значения средней температуры, достаточно знать лишь величину амплитуды и запаздывания во времени температурных колебаний в рассматриваемой точке конструкции для того, чтобы иметь полное представление об изменениях температурного поля за период колебаний внешних тепловых воздействий. В частности, теплофизический расчет ограждающих конструкций для летних условий, характеризующихся периодичностью прогрева при солнечном облучении и циклических повышениях температуры наружного воздуха, выполняется с учетом квазистационарных изменений температурного поля.
Во всех возможных случаях разработки приближенных инженерных методов расчета предпочтение отдается более простым и, в частности, основанным на рассмотрении закономерностей стационарного температурного поля. Иногда это приводит к некоторому повышению запасов теплофизической надежности рассчитываемых ограждающих конструкций, поскольку внешние воздействия, влияющие на распределение температур, приходится принимать наиболее неблагоприятными из числа закономерно возможных.
Так, например, теплофизический расчет ограждающих конструкций для холодного периода года проводится по условиям предельно возможного охлаждения конструкции, наступающего при таком наиболее низком значении температуры наружного воздуха, которое в соответствии с климатическими условиями может не изменяться в течение времени, необходимого для постепенной стабилизации наиболее неблагоприятного температурного поля в рассматриваемой конструкции.
Примечания
1. Эта функциональная раскрывается в дифференциальном уравнении Лапласа.
2. См. дифференциальное уравнение Фурье.