Минус в выражении (1.4) означает, что для получения положительной величины Q1 температура в направлении х должна уменьшаться, а не возрастать. Величина dt/dx, называемая градиентом температуры, выражается в град/м; λ — представляет коэффициент теплопроводности материала в ккал/м·ч·град.
При неустановившихся условиях количество тепла Q1, распространяющееся в направлении х, изменяется, что связано с поглощением или отдачей тепла частицами материальной среды при изменении их температуры с течением времени т (т. е. наличии величины dt/dx≠0.
Изменение потока тепла dQ1/dx пропорционально теплоемкости материала сγ (с — удельная теплоемкость в ккал/кг·град; γ — объемный вес материала в кг/мг); тогда
Знак минус в правой части уравнения означает, что повышение температуры материала связано с поглощением им тепла и соответствующим уменьшением теплового потока Q1.
Величина изменения потока тепла Q1 в направлении х может быть получена также дифференцированием уравнения (1.4), т. е.
При отсутствии внутренних источников или стоков тепла, изменение величины теплового потока связано только с поглощением тепла материалом, и выражения (1,5) и (1.6) должны быть равны. Из этого равенства выводится дифференциальное уравнение теплопроводности при одномерном распространении тепла в направлении х, а именно:
Это выражение известно как дифференциальное уравнение Фурье. Величина λ/cγ называется коэффициентом температуропроводности материала, имеет кинематическую размерность, в которую не входят измерители массы и энергии, и характеризует скорость перераспределения температуры, выражаемую обычно в м2/ч или см2/сут при нагреве или охлаждении материальной среды.
Материалы и конструкции с высоким коэффициентом температуропроводности быстро нагреваются или охлаждаются до температуры, соответствующей равновесному состоянию с окружающей средой.
В самом общем виде, при неустановившемся распространении тепла по всем трем осям координат, дифференциальное уравнение теплопроводности приобретает трехмерный вид:
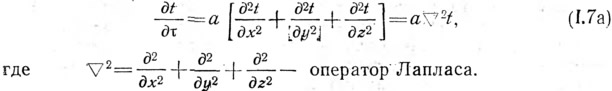
Путемч интегрирования одномерного (1.7), двухмерного или трехмерного уравнения теплопроводности могут быть получены любые конкретные решения, раскрывающие закономерности распространения тепла в материальных средах, в частности, ограждающих конструкциях зданий.
Чтобы получить из множества возможных конкретное решение, соответствующее определенному рассматриваемому процессу распространения тепла, необходимо располагать дополнительными условиями, не содержащимися в исходном дифференциальном уравнении. Эти дополнительные условия, которые вместе с исходным уравнением однозначно определяют все особенности рассматриваемого процесса, называются условиями однозначности1.
Условия однозначности разделяются на временные (характеризующие рассматриваемый физический процесс во времени) и пространственные, относящиеся к поверхностям, ограничивающим изучаемый объект или конструкцию, и особенностям физического процесса, происходящего на этих граничных поверхностях.
Различают три вида граничных условий:
- 1) граничное условие I рода, устанавливающее распределение температуры на поверхности и ее изменения во времени;
- 2) граничное условие II рода, устанавливающее величину потока тепла, проходящего через поверхность, и его изменения во времени;
- 3) граничное условие III рода, определяющее температуру окружающей среды и закон теплообмена между поверхностью и этой средой.
В строительной теплофизике обычно задаются граничные условия III рода, устанавливаемые значениями температуры среды t и коэффициентов теплообмена α2.
При рассмотрении теплопередачи в однородной среде и в установившихся условиях (когда dt/dτ=0), временные условия исключаются и значение имеют только пространственные.
В этих случаях, поскольку а≠0, уравнение (1.7а) приобретает вид:
Уравнение относится к температурному полю в установившихся условиях. Выражение (1.8) известно как уравнение Лапласа. Физический смысл этого уравнения состоит в том, что сумма изменений количеств тепла, поступающего к любой рассматриваемой точке конструкции, равна нулю. Следовательно, температуры ее неизменны и имеют установившиеся значения, отвечающие постоянным условиям воздействий внешней среды, окружающей конструкцию. При практических расчетах температурного поля проектируемых конструкций на основе уравнения (1.8) расчетные температуры внешней среды принимаются соответствующими возможности завершения процесса предельного охлаждения рассматриваемой конструкции. Этот процесс происходит постепенно и требует определенного времени: незначительного для легких конструкций и длительного — для массивных, поэтому расчетные значения температуры наружного воздуха в наиболее холодные зимние периоды зависят от степени массивности конструкции и связаны с возможностью более или менее длительной стабилизации теплового состояния во времени.
Для многих практических случаев достаточно исследования плоского температурного поля (в плане или разрезе конструкции). Для двумерных условий уравнение (1.8) имеет вид:
Исследование на основе уравнения (1.8а) температурных полей неоднородных в теплофизическом отношении облегченных конструкций (панелей с контурными ребрами, сопряжений крупных элементов ограждающих конструкций и т. д.) имеет весьма важное значение при проектировании индустриальных конструкций зданий, особенно в достаточно суровых климатических условиях, когда низкие температуры наружного воздуха длительны во времени и вызывают полное охлаждение, для которого характерно неизменное установившееся распределение предельно низких температур.
Порядок проведения подобных практических расчетов и применение для этих целей счетно-решающих устройств типа электроинтегратора, изложены далее в гл. IV.
Дифференциальное уравнение Фурье (1.7) в обобщающем смысле является уравнением нестационарного поля любого потенциала переноса (в данном случае — поля потенциала переноса тепла, т. е. температуры). С определенными ограничениями это уравнение может быть использовано и для изучения процессов влагообмена, происходящих в материальных системах при неизменной температуре.
Если рассматривать какую-либо материальную систему, например, ограждающую конструкцию, выполненную из влажного капиллярно-пористого материала и находящуюся в изотермической воздушной среде3, то за потенциал переноса влаги может быть принято влагосодержание материала (со, г/кг). Уравнение (1.7), записанное применительно к исследованию одномерного поля потенциала переноса влаги называют уравнением влагопроводности. Оно имеет вид:
где ω — влагосодержание материала (часто выражаемое через весовую влажность материала); аm — коэффициент нестационарной влагопроводности4, зависящий от природы материала и его влажностного состояния.
Уравнение влагопроводности, в частности, используется для обоснования простейших приближенных сравнительных расчетов длительности естественной сушки ограждающих конструкций из капиллярно-пористых материалов.
Примечания
1. Иногда условия однозначности называют краевыми условиями.
2. В теплотехнической литературе эти коэффициенты часто называют коэффициентами теплоотдачи, имея в виду особенности теплообмена материальных систем нагретых выше температуры окружающей среды.
3. То есть в среде с неизменной постоянной температурой.
4. Аналог коэффициента температуропроводности:
где х — коэффициент влагопроводности (г/кг·ед. потенц.) в установившихся условиях переноса, при заданном среднем влагосодержании материала; ξ — удельная влагоемкость материала (г/кг·ед. потенц.); γ — объемный вес (кг/м3).
