Рост размеров и усложнение формы конструкций, для многих из которых ветровая нагрузка стала доминирующей, вызвал потребность натурных наблюдений за сооружениями. Ветровая нагрузка изучалась по включенным в конструкцию индикаторам статических и динамических усилий. При этом записывались скорость и направление ветра по высоте, величина и направление перемещения конструкции. Такие наблюдения проводились иногда несколько лет, например за трубами тепловых электростанций, висячими мостами, радиомачтами. Были получены ценные материалы, но все же недостаточные по ряду соображений. Во многих наблюдениях не велась синхронная запись скорости ветра и деформаций конструкции. Часто ограничивались данными средней скорости ветра на высоте 10 м. Большинство наблюдений было сделано в условиях относительно слабых ветров, когда многие явления сглаживаются, при этом количественная оценка искажается. Можно указать и на ряд других обстоятельств, препятствующих установлению точных зависимостей между силой ветра и перемещением конструкции. Например, для правильной оценки профиля ветра по высоте ветроизмерительные приборы должны быть размещены на значительном расстоянии от конструкции, чтобы исключить искажения воздушного потока, вносимые сооружением. Часто длина рей была недостаточна.
В свете изложенного результаты многих натурных наблюдений имеют пока ценность для качественной оценки действительной работы сооружения при ветре.
Большую помощь в совершенствовании конструкций может дать тщательный анализ повреждений или аварий, если удается установить обстоятельства и истинную причину.
Наибольшая ветровая нагрузка на конструкции в виде круглого цилиндра, шара или на такие, у которых наблюдается кризис обтекания, может оказаться при меньшей величине скорости, чем расчетная. Это надо иметь в виду при проверке деформа-пивности сооружения. Например, если при расчетной скорости число Рейнольдса круглого цилиндра было 3,6-105 (за кризисом), а при расчете на деформативность оно оказалось 1,8·105 (до кризиса), то ветровая нагрузка приблизительно одинакова, несмотря на то что скорость ветра снизилась в 2 раза. Это следует из рис. 3.8. Такая же картина может быть, например, у шара, скругленных квадратных и прямоугольных цилиндров и тел, у которых наблюдается кризис обтекания, т. е. резкое снижение коэффициента сх.
Коэффициенты лобового сопротивления сх, подъемной силы cy и момента mz определяют экспериментально и относят к единице площади, а для длинных тел — к единице длины (размера) вдоль или поперек тела. При пользовании справочной литературой обращают внимание на величину удлинения тела, влияющего на величину аэродинамических коэффициентов (см. рис. 3.4). Желательны также сведения о шероховатости поверхности тела, также влияющей на его сопротивление.
Аэродинамическое сопротивление конструкций целесообразно рассматривать, начиная с простых по форме тел.
Полное сопротивление тонкой гладкой пластинки бесконечной длины, наклоненной к потоку, изменяется в зависимости от угла атаки, как это показано, например, на рис. 3.7. С достаточной точностью коэффициент лобового сопротивления можно принять пропорциональным 1,1 sin2α, где α — угол атаки. Это хорошо удовлетворяется для углов атаки 40—60°, а при α<35° коэффициент лучше повысить до 1,2 sin2 α.
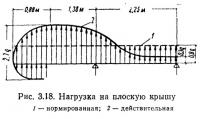
В ряде случаев расчета необходимы полное сопротивление, координаты центра давления или коэффициент аэродинамического момента. Например, для плоских крыш зданий, открытых навесов с пологими крышами лобовое сопротивление может быть малым, но распределение давления по крыше неблагоприятно (рис. 3.18), в результате чего они срываются ветром. Причина опрокидывания мостов со сплошным настилом проезжей части кроется отчасти в пренебрежении подъемной силой.
При спокойном рельефе местности конструкции рассчитывают при направлении ветра под углом к горизонту не менее ±10°.
При исследовании на моделях угол атаки расширяют до ±20°. В сильнопересеченной местности или в горных районах ветер может отклоняться от горизонтального на ±20° и более. В городах возможны углы атаки еще больше и даже противоположное основному местное направление потока.
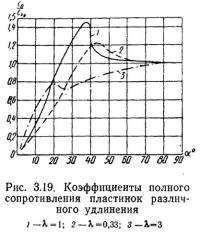
Ветровая нагрузка на прямоугольную пластинку зависит от расположения ее по отношению к скорости потока: длинной стороной по потоку или поперек его. На рис. 3.19 приведены графики относительного коэффициента полного сопротивления пластинок с удлинением 0,33; 1 и 3 в зависимости от угла атаки. Как видно, коэффициент полного сопротивления квадратной пластинки при угле атаки около 38° в 1,46 раза больше коэффициента лобового сопротивления пластинки при угле атаки 90°. По другим данным (Геттинген), он больше в 1,6 раза. Далее, с ростом угла атаки ее сопротивление резко падает. Изменение направления ветра в окрестности угла α=38° приводит к дополнительному — динамическому — воздействию, например на поддерживающую плоский щит конструкцию вследствие срывов потока. Это явление аналогично срывному флаттеру крыла самолета.
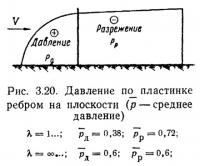
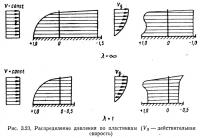
Для определения аэродинамических коэффициентов модель подвешивают к весам, т. е. располагают ее изолированно от стенок трубы. При установке тонкой пластинки ребром на плиту или дно трубы характер ее обтекания по сравнению с изолированной существенно изменяется в тыльной (подветренной) стороне. Давление на лицевую сторону пластинки изменяется мало (рис. 3.20). Коэффициент лобового сопротивления такой бесконечной длинной пластинки равен всего 1,2 вместо 1,98—2,12 той .же пластинки, но изолированной. Коэффициент лобового сопротивления установленной ребром квадратной пластинки, как следует из физических представлений, изменяется мало, по опытам, он равен 1,1 вместо 1,2 у изолированной пластинки.
Распределение давления по высоте тела зависит от профиля скорости потока вблизи тела. К верхнему краю пластинки давление снижается вследствие увеличения скорости потока, обтекающего ее верхний край. Если пластинка конечной длины, то у ее боковых краев будет аналогичное явление, в результате чего давление в верхней части еще более снизится. У самого края передней стороны пластинки будет разрежение, величина которого будет тем больше, чем она длиннее. У края длинной пластинки давление от разрежения в 1,38 раза больше скоростного напора. Это весьма важное обстоятельство учитывают при проектировании зданий с тонкостенными ограждающими элементами, повышая расчетную нагрузку у краев зданий или навесов.
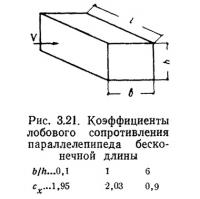
С утолщением пластинки, когда она перерастает в бесконечно длинный параллелепипед, характер обтекания изменяется, коэффициент ее лобового сопротивления падает тем сильнее, чем. больше его размеры (толщина) в направлении потока (рис. 3.21).
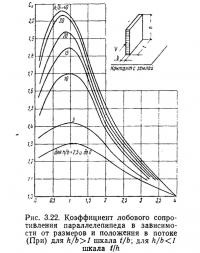
Для суждения о лобовом сопротивлении сложной по форме сплошностенчатой конструкции можно воспользоваться коэффициентами лобового сопротивления параллелепипеда, стоящего на плоскости (рис. 3.22). Этот рисунок позволяет оценить ветровую нагрузку при различном отношении размеров тела и учесть его положение относительно направления потока.
Аэродинамические коэффициенты бесконечно длинных тел — цилиндров различного неизменного по длине сечения, характерных острыми краями и плоскими гранями, приведены в табл. 3.1. Коэффициент лобового сопротивления многих стержней мало зависит от формы поперечного сечения и близок к коэффициенту сопротивления плоской пластинки. У несимметричных профилей появляется подъемная сила, которая, суммируясь с лобовым сопротивлением, увеличивает нагрузку на тело. Например, у тела в виде равнобокового уголка коэффициент cR=2,76 (отнесен к ширине полки).
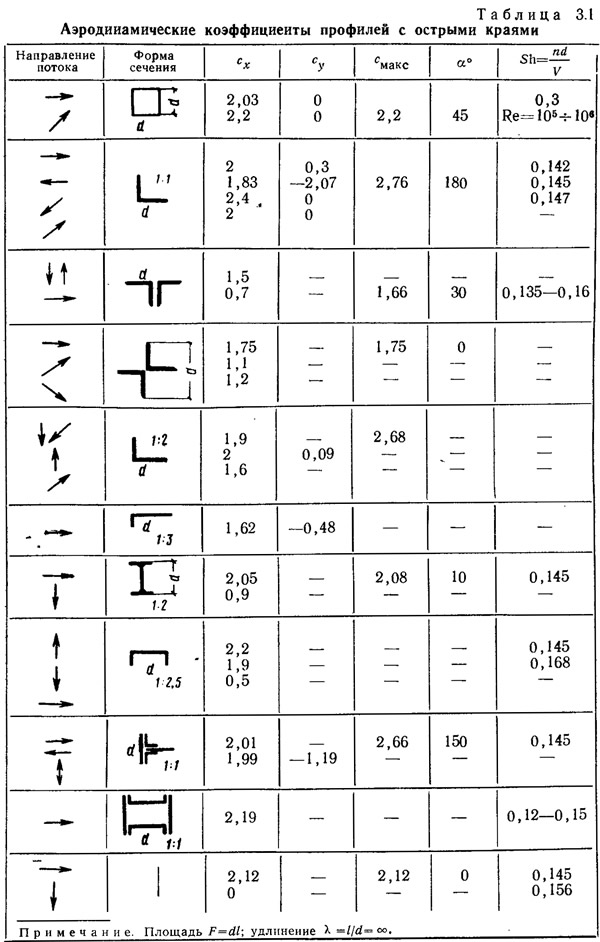
Сходство картины обтекания тел различных профилей с острыми краями с обтеканием плоской пластинки позволяет принять одну и ту же закономерность снижения коэффициента лобового сопротивления в зависимости от удлинения тела (см. рис. 3.4).
В расчете решетчатых конструкций величина коэффициента лобового сопротивления для всех видов профилей, за исключением круглого, принимается 1,4 (по СНиП), за рубежом этот коэффициент — 1,6 и более.
Отрицательное давление на поверхность тела в зоне разрежения чаще больше положительного (избыточного) давления у его передней критической точки. Это наблюдается у краев сплошно-стенчатых конструкций или зданий. Например, высотное здание разрушилось при урагане, потому что действительное распределение ветровой нагрузки по поверхности (стене) не отвечало принятому в проекте, хотя в момент аварии среднее значение ее было меньше расчетного. В нормах обычно указывается ветровая нагрузка в виде осредненной по площади, в то время как в большинстве случаев распределение нагрузки сложнее хотя бы из-за другого профиля скорости по высоте (рис. 3.23).
Для тонкостенных конструкций, большепролетных перекрытий, особенно с легкими ограждающими элементами, знание действительного распределения давления по поверхности обязательно. В конструкциях покрытий с несущими канатами, т. е. в конструкциях с односторонними связями, это особенно важно, так как в некоторых местах нагрузка окажется противоположного направления по сравнению с принятым в расчете.
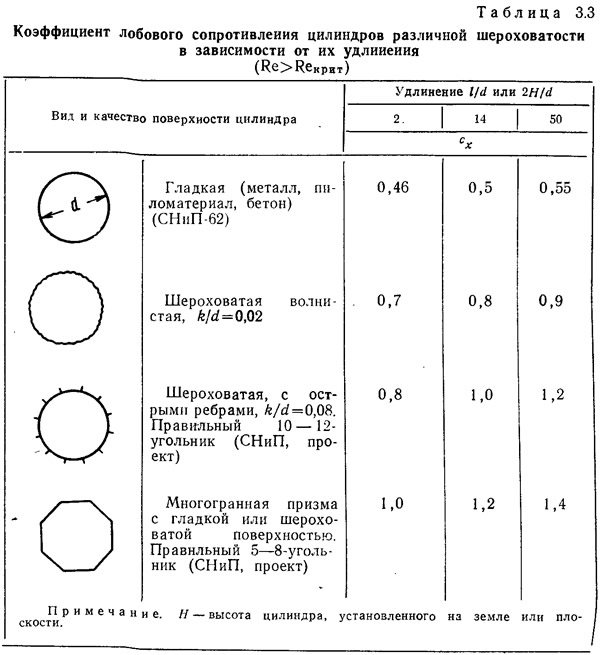
Распределение, давления по поверхности круглого цилиндра зависит от числа Рейнольдса (см. рис. 3.12), а при небольшом удлинении — и от его величины; чем меньше удлинение цилиндра, тем разрежение позади меньше; давление спереди изменяется мало. Для гладкого круглого цилиндра при закризисном обтекании коэффициенты распределения давления по его поверхности приведены в табл. 3.2. Этими данными пользуются при определении местной нагрузки по круглому цилиндру, а также с известным допущением — по многогранным призмам. Коэффициент лобового сопротивления таких тел в зависимости от удлинения берется по табл. 3.3, а для шероховатых круглых цилиндров — по рис. 3.15. В последней строке табл. 3.2 даны коэффициенты распределения давления по шару, когда его коэффициент лобового сопротивления равен 0,2, т. е. также при закризисном обтекании. Наименьший коэффициент лобового сопротивления гладкого шара cx=0,08.

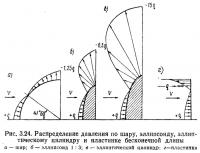
На рис. 3.24 приведено распределение давления по поверхности тел, характерных различным радиусом скругления краев — кривизной поверхности. Как видно, отрицательное давление у всех тел во много раз больше давления у их передней критической точки, где оно равно скоростному напору. Форма тела, его удлинение и кривизна поверхности у его краев играют доминирующую роль в величине и характере распределения давления в области разрежения: чем больше относительное удлинение и меньше радиус закругления краев тела, тем величина разрежения у краев больше. Отсюда следует, что небольшим увеличением радиуса закругления тела можно снизить лишь местную нагрузку на него, общее сопротивление изменится незначительно. Наоборот, у стержня в виде полукруглого цилиндра (удлинение 8), расположенного выпуклой стороной к потоку, т. е. с полностью скругленной передней стенкой, коэффициент лобового сопротивления равен 0,64, а расположенного плоской стороной к потоку — 1,28. Коэффициент лобового сопротивления стержня треугольного сечения (удлинение 8) увеличивается также примерно вдвое: при направлении потока по нормали к грани коэффициент сх=1,25, при направлении на угол он равен 0,58. При углах атаки α=7° и α=—73° коэффициент подъемной силы треугольного стержня наибольший, он равен около 1,0. Коэффициент сх бесконечно длинного треугольного цилиндра при потоке на грань равен 2,05, на угол — 1,25.
В решетчатых конструкциях, составленных из стержней разнообразного профиля и расположенных к тому же под различными углами к направлению ветра, пользуются осредненным коэффициентом лобового сопротивления. При исследовании решетчатых конструкций в аэродинамической трубе модели часто выполняют из равновеликих по наветренной площади плоских полос, что проще.