Элементы аэродинамики строительных конструкций

Начало аэродинамики как науки связано с именами Д. Бернулли и Л. Эйлера, работавших в Петербургской Академии наук. Большой вклад в эту науку внесен Н. Е. Жуковским и С. А. Чаплыгиным. Развитие аэродинамики было обусловлено по преимуществу запросами самолетостроения. В этом направлении достигнуты огромные успехи, чему свидетельство — современные самолеты. Вопросы аэродинамики строительных конструкций и зданий не получили должного освещения и развития, несмотря на огромные масштабы строительства и большое значение этого раздела науки в расчете прочности высоких сооружений и зданий, большепролетных конструкций и мостов.

Большое разнообразие конструкций не позволяет дать исчерпывающий ответ на поведение их в потоке. В этой связи полезны общие сведения из аэродинамики.

Воздух — вязкая сжимаемая среда. Полный учет этих особенностей среды даже при современном состоянии математического анализа не может быть сделан ввиду непреодолимых трудностей решения дифференциальных уравнений Навье — Стокса с надлежащими граничными условиями¹. При решении многих задач можно отказаться от учета сжимаемости и рассматривать воздух как вязкую среду. Решение значительно упрощается, но все же остается достаточно сложным.

В ряде случаев пренебрегают и вязкостью среды, рассматривая воздух как идеальную несжимаемую жидкость, т. е. такую,, в которой все напряжения остаются нормальными, а касательные (тангенциальные) — отсутствуют. Привлекая к решению» экспериментальные данные, получают с достаточной для практических целей точностью близкую к действительности картину.

Для изучения поведения плохо обтекаемых тел, к которым относятся строительные конструкции, лишь в редких случаях удается решить задачу, рассматривая воздух в виде несжимаемой идеальной жидкости. Поэтому преобладающее значение приобретает экспериментальная аэрогидродинамика, базирующаяся на теории. Знания теоретической аэродинамики нужны также для правильной постановки задачи и для опытов в аэродинамической трубе или водяном канале. Течение жидкости удобно наблюдать, визуализируя воздушный поток шелковинками, наклеиваемыми на модель, различными легкими порошками на поверхности воды, пузырьками газа, образующегося при электролизе воды при опытах в водяном канале, и др.


Воздух — сжимаемая жидкость, что проявляется в изменении его параметров (плотности, давления) с увеличением скорости: потока в сравнении с теми, которые были бы в предположении несжимаемости. Особенно быстро происходят эти изменения параметров, когда скорость движения жидкости приближается к скорости звука. Для интересующей строителя области задай можно с достаточным приближением принять, что при скорости потока до 100 м/сек параметры воздуха остаются неизменными. Наибольшие скорости ветра, наблюдаемые на земле, 70 м/сек; лишь в горах и в Антарктике они достигают 100 м/сек. Поэтому для упрощения исследования условно можно считать воздух несжимаемой жидкостью.

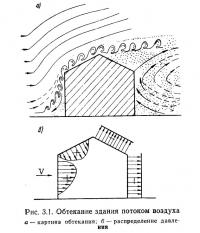
Как показывают многочисленные наблюдения, движение воздуха может быть упорядоченным, т. е. ламинарным (слоистым), когда не происходит взаимного перемешивания жидкости смежных слоев. Иначе это движение называют движением жидкости без пульсации скоростей. Турбулентное движение, при котором: все время происходит перемешивание частиц вследствие изменений скорости, плотности, давления и температуры, наблюдается вблизи обтекаемых потоком тел или у поверхности земли (рис. 3.1). В основном оно объясняется потерей устойчивости ламинарным течением. Средние скорости вблизи поверхности возрастают от нулевой до скорости, равной скорости вдали.

Скорость в данной точке при турбулентном движении чаще всего принимают среднюю, что упрощает исследования. Действительное движение воздуха — чрезвычайно сложное, поэтому в расчет вводят ряд упрощений.

При решении задач о силовом воздействии среды на тело и тела на среду можно отказаться от молекулярных движений, накладывающихся на основной поток и тем самым осложняющих исследования. Это позволяет принять воздух как непрерывную сплошную деформируемую среду.


Плотность воздуха при нормальном барометрическом давлении (760 мм рт.ст.) и температуре 15°С равна 0,125 кг·м^—4·сек². Состояние воздуха при таком давлении и температуре принимается за стандартную атмосферу, к которой приводят результаты опытов. Это позволяет сравнивать данные исследований, проведенных при различных вариациях давления и температуры.

При нестандартных параметрах плотность воздуха


где ρ₀ — плотность воздуха стандартной атмосферы;
p — барометрическое давление в мм рт. ст.);
t° — температура в °С.

Как видно, зависимость плотности воздуха от давления и температуры близка к линейной в приземном слое.

С отличной от стандартной плотности воздуха приходится считаться при строительстве в высокогорных районах, на Крайнем Севере. Строго говоря, в формулу (3.1) необходимо вводить поправку на влажность воздуха, хотя она существенно влияет только при температуре более 20° С. Это учитывают при большой влажности воздуха в тропиках.

Для выяснения связи между скоростью и давлением воздуха в потоке можно с достаточной точностью оперировать формулами идеальной жидкости. Тогда эта связь устанавливается уравнением Д. Бернулли


где р — давление в потоке, называемое статическим;


ρV²/2 — скоростной напор жидкости, иногда называемый динамическим напором.

Уравнение (3.2) указывает па постоянство суммарного или полного давления в любом месте потока. Оно справедливо только для установившегося движения жидкости.

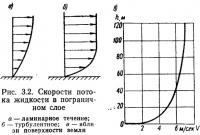
При движении воздуха, т. е. вязкой жидкости, возникают силы внутреннего трения или силы вязкости. Они проявляются, например, в падении давления в трубах в направлении течения. Эти касательные силы существуют не только между жидкостью и телом в потоке, стенкой трубы или канала, но и между отдельными слоями жидкости с разной скоростью. Слой жидкости, непосредственно прилегающий к телу, трубе, каналу, не движется, он тормозит смежный с ним слой, который действует таким же образом на следующий, и т. д. Скорость вблизи тела возрастает от нулевой у его поверхности до скорости невозмущенного потока вдали (рис. 3.2). Толщина этого слоя, называемого пограничным, мала; она тем меньше, чем больше скорость потока. Пограничный слой оказывает огромное влияние на поведение тела в потоке.

Силы трения пропорциональны вязкости жидкости и градиенту скорости потока. Коэффициент вязкости μ определяется опытным путем. У воздуха при температуре 15°С он равен 1,81·10^—4 пз, у воды — 1,1·10^—2 пз.

При небольшой скорости жидкости сила трения не зависит от шероховатости поверхности тела (трубы, канала), потому что слой непосредственно у тела как бы прилипает к нему и основную роль играет трение жидкости в пределах пограничного слоя. С увеличением скорости толщина пограничного слоя уменьшается, размеры неровностей — отдельные зерна или волны — становятся соизмеримыми и даже больше толщины пограничного слоя; роль силы трения снова возрастает. Это приводит к увеличению сопротивления тела при больших скоростях жидкости Силы трения нарушают справедливость уравнения Бернулли в том смысле, что величина постоянной в формуле (3.2) изменяется, например уменьшается с приближением к поверхности обтекаемой стенки.


Если силы трения, отнесенные к единице объема, значительно меньше кинетической энергии того же объема жидкости, или иначе


где V — скорость потока; l — характерный размер тела (например, диаметр трубы), то ими можно пренебречь.

Отношение энергии элементарного объема движущейся жидкости к работе сил вязкости, являющееся безразмерной величиной,


называется числом Рейнольдса; чем оно больше, чем меньше влияние сил вязкости.

Число Рейнольдса играет огромную роль, так как характеризует ламинарное или турбулентное движение жидкости. Размеры строительных конструкций велики, как и скорости ветра, поэтому силами вязкости пренебрегают. Это дает право применять уравнение (закон) Бернулли при исследовании поведения тел в потоке в областях плавного обтекания, в зонах за местами срыва потока уравнение Бернулли неприменимо.

При исследовании тождественную прототипу картину обтекания геометрически подобной и одинаково расположенной в потоке модели можно получить, приравняв их числа Рейнольдса.

Более существенную роль играет не коэффициент вязкости, а отношение μ/p, называемое кинематическим коэффициентом вязкости, его обозначают v. Для воздуха стандартной атмосферы v=14,6·10^—6 м²/сек (обратная величина 68500). При условии температурного градиента на каждые 1000 м высоты над уровнем моря 6,5°, коэффициент v=15,20·10^—6 на высоте 500 м и 15,80·10^—6 на высоте 1000 м. Несмотря на то, что коэффициент вязкости воды на два порядка больше, чем воздуха, коэффициент v воды в 10 раз меньше вследствие большей плотности. Это облегчает моделирование при проведении опытов в водяном канале, если необходимо соблюдать равенство чисел Рейнольдса модели и прототипа.


Одна из основных задач аэродинамики — определение сил и моментов, действующих на тело в потоке. В силу сложности теоретического исследования особое значение приобретает эксперимент. Для этого тело закрепляют в рабочей части аэродинамической трубы или водяного канала с помощью динамометров или к аэродинамическим весам, способным измерять составляющие общей (полной) результирующей силы и момента, действующие на тело. Этот прием исследования носит название весового способа.

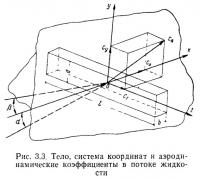
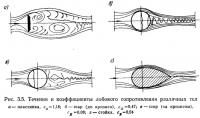
В аэродинамике чаще всего принята правая прямоугольная система координат, связанная со скоростью (поточная система координат) , когда координатные оси направлены: ось х — по потоку (скорости), ось у — перпендикулярно оси х и вверх, если смотреть сбоку на поток, ось z — перпендикулярно осям х и у (рис. 3.3).

В общем случае результирующая сила воздействия потока на тело имеет составляющие, направленные по всем осям. Составляющую этой силы по оси х называют лобовым сопротивлением и обозначают X, составляющую по оси у — подъемной силой, обозначаемой Y, составляющую по оси z называют боковой силой Z.

Лобовое сопротивление тела является суммой лобового сопротивления давления, зависящего от формы тела, и лобового сопротивления трения, взятых по всей поверхности тела.

Вообще, результирующая сила не проходит через начало координат; тогда возникают моменты относительно осей х, у и z, стремящиеся повернуть тело. Их определяют также с помощью аэродинамических весов.

В общем случае величины составляющих сил и моментов их зависят от тела (форма, величина, ориентация в потоке и т. д.), среды (плотность, давление, состояние среды и т. д.) и движения (величина скорости). В упрощенном виде величины сил и моментов воздействия среды на тело представляются только в виде зависимости от плотности среды, размеров тела и скорости движения. Во многих случаях шероховатость поверхности тела существенно влияет на характер обтекания тела потоком и на величину этих сил.

Положение тела определяется углом, под которым на него набегает поток. Угол, образованный проекцией вектора скорости потока на плоскость симметрии объекта с осью объекта х, называют по традиции углом атаки а. Значения угла а считают положительными, когда он образован поворотом объекта против часовой стрелки. При косой обдувке, т. е. когда объект повернут относительно первоначального положения в плоскости ху, угол между вектором скорости потока и плоскостью симметрии ху называют углом скольжения β. Он положителен, когда объект повернут против часовой стрелки для наблюдателя, стоящего у конца оси у. Если объект не имеет плоскости симметрии, тогда одно из характерных сечений принимается за исходное. При других правилах отсчета они должны быть оговорены.

В ряде случаев применяют систему прямоугольных координат, связанную с исследуемым телом. Их осям х', у' и z' придают индекс в виде штриха или обозначают соответственно n, t и z. При симметричной картине обтекания связь между аэродинамическими силами в скоростных (поточных) осях координат с силами (коэффициентами) в осях, связанных с исследуемым телом, устанавливается следующими соотношениями:


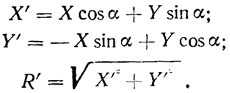
Более полное представление о силах воздействия потока жидкости на тело дает распределение сил по поверхности модели. В частности, для определения нормальных сил в характерных местах модели делают небольшие отверстия, давления в которых измеряют при помощи батарейного жидкостного манометра, соединенного трубками с каждым отверстием. Для плохо обтекаемых тел часто ограничиваются измерением нормальных к поверхности сил, а касательными, вызванными вязкостью среды, пренебрегают, считая их малыми.

Стационарные аэродинамические силы, действующие на тело в потоке, зависят также от свойств и состояния среды, формы, размеров и качества поверхности (шероховатости) тела и в общем случае — от скорости потока. Со сжимаемостью не считаются, поскольку она сказывается при скоростях, значительно больших наблюдаемых в свободной атмосфере².

При этих допущениях сопротивление тела потоку воздуха можно записать в виде


где l — характерный размер тела;
V — скорость потока;
Ф — некоторая функция величин, заключенных в скобки. Если принять скоростной напор


а за характерный размер тела — определенную площадь S, то выражение (3.4) принимает вид


Рассматривая явления, происходящие в стандартной атмосфере, т. е. полагая ρ=0,125 кг·сек²/м⁴, можно переписать, обозначая выражение в скобках формулы (3.5) через коэффициент c_R


где V — в м/сек; S — в м₂.

Коэффициент c_R, называемый коэффициентом полного сопротивления, зависит так же, как аэродинамическая сила, от свойств тела, среды и движения. Для геометрически подобных тел при одинаковой ориентации в потоке коэффициент c_R зависит в общем случае и от величины числа Re.

Для длинных тел с неизменным поперечным сечением по длине, расположенных поперек потока, коэффициент c_R относят к единице длины тела. Тогда выражение (3.6) принимает вид


где d — характерный размер тела, например диаметр трубы или ширина пластинки;
L — длина тела.

Коэффициент c_R, являющийся аэродинамической характеристикой тела, находят опытным путем с помощью аэродинамических весов или зная распределение давления по поверхности тела.

Взвешиванием определяют отдельно лобовое сопротивление Q и подъемную силу Р. Тогда полное сопротивление симметричного тела


а коэффициент полного сопротивления

где коэффициент лобового сопротивления

а коэффициент подъемной силы

Здесь S — площадь проекции тела на плоскость, нормальную к направлению потока жидкости, в м².

При косой обдувке тела появляется составляющая боковой силы c_z, тогда коэффициент


Коэффициенты аэродинамического момента обозначают m_x, m_y и m_z. При прежних обозначениях они определяются из выражения


где j=x, у, z — в зависимости от осей, относительно которых определяется момент.

Во многих случаях рассматривают более простую — двухмерную задачу, когда поток плоскопараллельный и картина обтекания одинакова по всей длине тела. Имитация бесконечно длинного тела достигается постановкой на концах модели тонких шайб большого размера, препятствующих затеканию жидкости с торцов, либо упором модели в стенки трубы с рабочей частью прямоугольного сечения.

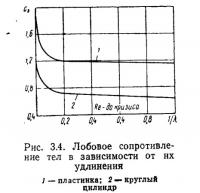
Коэффициент лобового сопротивления тела, отнесенный к единице его длины (размер поперек потока), увеличивается с ростом удлинения λ= l:d [здесь l — длина тела, a d — характерный размер (диаметр трубы, сторона квадрата, треугольника и др.)], асимптотически приближаясь к предельному значению при λ=∞ (рис. 3.4).

Пластинка представляет собой элементарное тело, исследование поведения которого облегчает понимание механизма явлений, происходящих с более сложными по форме телами.

Рассмотрим жесткую тонкую пластинку (толщина пластинки не более 0,01—0,02 ее ширины), помещенную в поток реальной жидкости. При угле атаки α=0° (пластинка по потоку) ее лобовое сопротивление определяется в основном силой трения, вызванной вязкостью среды. При угле атаки α=90° и числах Рейнольдса до Re=1000, т. е. при очень малых скоростях потока, сопротивление пластинки сильно зависит от числа Рейнольдса, в котором под характерным размером пластинки понимается ее ширина. При дальнейшем увеличении Re коэффициент лобового сопротивления пластинки не зависит от величины числа Re. Это чрезвычайно важное обстоятельство, позволяющее при моделировании не выполнять требований равенства чисел Рейнольдса модели и прототипа, значительно облегчает исследования.

Сопротивление пластинки при угле атаки α=90° складывается из сил избыточного давления³ (положительное давление) на переднюю сторону и сил давления от разрежения (отрицательное давление) на задней — тыльной стороне. Большую роль в величине лобового сопротивления пластинки играют силы давления от разрежения.

Из простых физических представлений следует, что при угле атаки α=90° наименьший коэффициент лобового сопротивления прямоугольной пластинки с отношением сторон 1:1, численно он равен 1,18, по данным опытов. В этом случае разрежение позади пластинки становится меньше, чем при больших удлинениях. Коэффициент лобового сопротивления пластинки растет с удлинением и при бесконечной длине становится равным 1,98—2,12⁴ (см. рис. 3.4). Важно, что сопротивление пластинки начиная с удлинения 10 быстро возрастает.

При обтекании плоской пластинки, расположенной по потоку (угол атаки α=0°), ламинарное течение в пограничном слое поддерживается на длине считая от передней кромки, определяемой числом Рейнольдса 3·10⁵—5·10⁵. После этого течение переходит в турбулентное. Точка перехода ламинарного пограничного слоя в турбулентный с увеличением числа Рейнольдса перемещается от задней кромки пластинки к передней. Сопротивление пластинки растет, и наибольшим оно становится, когда точка (зона) отрыва приближается к передней кромке. Важно отметить, что чем дольше сохраняется ламинарное течение вдоль пластинки, тем меньше ее сопротивление. Поэтому задача создания хорошо обтекаемых тел заключается в выборе такого профиля, у которого переход в турбулентное обтекание или отрыв вихрей происходит вблизи задней кромки тела.

Визуализацией потока у пластинки, расположенной нормально к нему, установлено, что течение у ее краев срывается; за пластинкой образуются вихри, уносящиеся затем потоком. Течение жидкости у задней стороны пластинки и вблизи ее оси направлено против потока (рис. 3.5). Позади пластинки образуется область пониженного давления, величина которого до больших углов атаки постоянна почти до краев пластинки (рис. 3.6). Спереди наибольшая разность давления наблюдается у оси пластинки — у передней критической точки. К краям пластинки давление падает и у краев становится отрицательным (меньше статического вдали). Средняя разность давления впереди квадратной пластинки равна приблизительно 0,38, а позади — 0,8 скоростного напора, в то время как у бесконечно длинной пластинки она равна соответственно 0,6 и 1,38. По СНиП коэффициент с_х пластинки принимают 1,4, при этом считают +0,8 на наветренную сторону и —0,6 — на подветренную.

Характерно, что для углов атаки от 90° до приблизительно 15° давление на заднюю сторону пластинки, уменьшаясь по абсолютной величине, остается примерно постоянным по всей ее ширине (см. рис. 3.6). С уменьшением угла атаки а центр давления по лицевой стороне приближается к передней кромке. В результате этого на пластинку будет действовать аэродинамический момент относительно оси г, проходящей через центр тяжести,


где b — ширина пластинки.

Момент М_z или коэффициент m_z будут равными нулю при углах атаки α=0 и 90°.

При углах атаки α≠0 или 90°, а также при косой обдувке, когда угол скольжения β≠0°, пластинка подвергается скручиванию, поскольку центр давления (сопротивления) переместился по направлению к ее передней кромке.

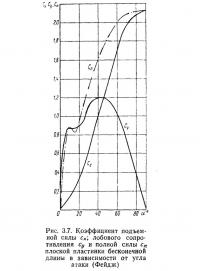
Сопротивление пластинки при угле α=90° определяется суммарным давлением (разрежением), нормальным к ее поверхности, поскольку при больших числах Рейнольдса сопротивление трения значительно меньше. При углах атаки а≠90° нормальная (результирующая) сила больше лобового сопротивления пластинки (рис. 3.7). Это учитывают в расчете тонкостенных конструкций, как и то, что силы давления на поверхность тела в зоне разрежения (изнутри) часто значительно больше, чем силы давления у передней критической точки (извне).

Центр давления на наклоненную к потоку пластинку с увеличением угла атаки от нуля до α=10÷15° перемещается от ее передней кромки до расстояния 0,4·b, где b — ширина пластинки. Далее эксцентриситет равнодействующей силы уменьшается и при углах атаки α>45° приближается к нулю.

Одними из ранних опытов по выяснению лобового сопротивления тел в потоке жидкости были опыты с гладким шаром. Начиная с числа Re=5·10³, при котором коэффициент лобового сопротивления шара наименьший в этой зоне чисел Re, коэффициент сопротивления его с ростом Re остается постоянным и равным 0,5. Около Re=3·10⁵ коэффициент сопротивления шара резко падает до 0,08, а затем медленно повышается (рис. 3.8). Область резкого падения коэффициента лобового сопротивления, называемая областью кризиса, перемещается в зависимости от степени турбулентности потока⁵; она наступает тем раньше, чем больше турбулентность потока. При числах Рейнольдса меньше 5·10³ коэффициент лобового сопротивления шара растет с уменьшением Re. При числе Re<1 он становится более 100. Эта область течения имеет теоретический интерес для строителя. Лобовое сопротивление шара в докризисной области может быть понижено, если на него надето кольцо (Прандтль), которое турбулизирует поток и тем переводит его обтекание как бы в закризисную область, в которой коэффициент лобового сопротивления шара значительно меньше, чем до кризиса.

Большой интерес представляет изучение поведения круглого цилиндра в потоке жидкости, поскольку такая форма часто встречается в строительных конструкциях, машиностроении и других областях техники.

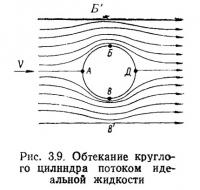
Сначала рассмотрим круглый цилиндр в потоке идеальной, т. е. невязкой, жидкости, ось которого направлена нормально к скорости потока (рис. 3.9). Статическое давление вдали от цилиндра р₀, а скорость потока V. Линии тока жидкости обтекают цилиндр одинаково относительно вертикальной и горизонтальной осей симметрии. В точке А, называемой передней критической точкой, где происходит разветвление линий тока, скорость равна нулю, а давление больше, чем вдали от тела.

В точках Б и В, где линии тока сгущаются, скорость становится больше, чем в набегающем потоке, а давление меньше, чем в потоке вдали от тела. Если предположить, что на расстоянии, равном радиусу цилиндра (точки Б' и В'), сгущение линий тока уже незначительно, то скорости потока в точках Б и В будут равны 2V, чтобы пропустить через уменьшенное вдвое сечение Б'В' тот же объем жидкости.

Поскольку силы вязкости отсутствуют, можно применить уравнение Бернулли (3.2). Тогда давление в точке А


таккак V_A=0.

Давление в точках Б и В найдется из уравнения


При

уравнение (3.12) принимает вид

откуда

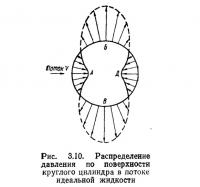
Из уравнения (3.13) видно, что отрицательное давление в точке Б или В приблизительно в 3 раза больше положительного (избыточного) давления в точке А. Далее, частицы жидкости, обладая достаточной кинетической энергией и при отсутствии сил трения, создадут в точке Д, где скорость равна нулю, давление, равное давлению в точке А (рис. 3.10).

Из картины обтекания симметричного тела идеальной жидкостью видно, что поток не оказывает силы сопротивления телу (парадокс Эйлера): вследствие симметрии обтекания равнодействующая сила равна нулю, хотя во всех точках по периметру цилиндра силы нормального давления действуют на стенки цилиндра (направление сил показано на рис. 3.10 стрелками).

Действительные жидкости обладают вязкостью, поэтому не может быть полного (плавного) обтекания. В результате влияния сил вязкости поток реальной жидкости оказывает телу сопротивление. Это происходит потому, что слой, непосредственно прилегающий к цилиндру, не скользит свободно, а как бы прилипает к стенке, в результате чего возникают тангенциальные силы, направленные по касательной к поверхности тела. Эти силы и являются собственно силами трения. У воздуха они малы, поэтому при незначительном изменении картины обтекания сила сопротивления в реальной жидкости мало отличалась бы от нуля. Важно то, что силы вязкости вносят качественные изменения в картину обтекания.

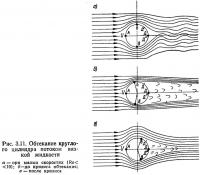
Силы вязкости приводят к отрыву пограничного слоя и образованию позади тела вихреобразного движения жидкости (рис. 3.11). Давление вязкой жидкости на цилиндр у точки А почти не отличается от давления при обтекании его идеальной жидкостью. Существенно то, что движение в пограничном слое тормозится и частицы жидкости приходят в точки Б и В с меньшими скоростями, чем в случае обтекания идеальной жидкостью, т. е. они будут обладать меньшей кинетической энергией. В точках Д' и Д" давление поэтому будет больше, чем в точках Б и В, но меньше p_A. В результате этого струи воздуха отрываются от цилиндра, так как не могут проникнуть в область Д'ДД", заполненную вихреобразно движущейся жидкостью с давлением Р_Д<Р_A.

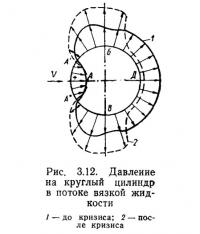
Как видно на рис. 3.12, распределение давления по поверхности цилиндра при обтекании его потоком вязкой жидкости существенно отличается в области задней половины цилиндра от картины при обтекании идеальной жидкостью (см. рис. 3.10). Равнодействующая распределенных сил, действующих на стенки цилиндра, становится не равной нулю. Эту силу называют лобовым сопротивлением, составляющими которого являются силы трения и собственно давление.

Отрыв пограничного слоя вносит качественное изменение в обтекание тела потоком жидкости, которое не ограничивается лишь появлением лобового сопротивления, а сопровождается образованием вихрей, срывающихся с цилиндра и уносящихся потоком жидкости. Они рассеиваются далеко позади цилиндра. Явление вихреобразования происходит так: по любой нормали к поверхности цилиндра скорость жидкости постепенно возрастает от нулевой, которую имеет слой, непосредственно прилегающий к стенке, до скорости потока за пределами пограничного слоя, толщина которого мала. На рис. 3.2, а показано распределение скоростей при ламинарном течении в пограничном слое, а на рис. 3.2, б — при турбулентном течении, которое характеризуется более быстрым нарастанием скоростей у пластинки.

Объем жидкости в пограничном слое обладает моментом количества движения относительно оси, нормальной к плоскости потока и проходящей через центр объема. Такое движение жидкости обладает завихренностью, поэтому наряду с поступательным движением объема жидкости происходит и вращательное движение. Топкие слои неустойчивы, они распадаются на отдельные вихри, уносимые потоком. Вихри располагаются за цилиндром в шахматном порядке (рис. 3.13), так как симметричное расположение вихрей — один над другим в дорожке — неустойчиво, что подтверждается многочисленными опытами и наблюдениями натуры. Вихри срываются не только с круглого цилиндра, но и с тел любой формы. Вихревую дорожку за круглым цилиндром называют дорожкой Бенара — Кармана, а часто — просто Кармана.

Подобная же картина распределения скоростей воздушного потока наблюдается у поверхности земли (см. рис. 3.2, в). Градиент скорости ветра уменьшается по мере удаления от поверхности земли, т. е. поток воздуха с высотой делается более равномерным.

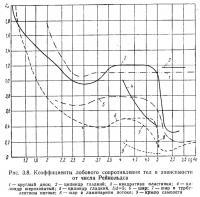
Опыты по продувке гладких круглых труб — цилиндров <ЦАГИ, Геттинген и др.) показывают, что коэффициент лобового сопротивления сх в интервале чисел Рейнольдса приблизительно Re=1,6·10⁴÷1,8·10⁵ остается примерно постоянным и равным 1,2, затем резко падает в области Re=1,8·10⁵÷3,5·10⁵ (см. рис. 3.8), достигает минимума при Re=5,5·10⁵, а потом он медленно возрастает. Для гладкого полированного круглого цилиндра наименьшее значение коэффициента с_х равно 0,3. Область резкого падения коэффициента с_х называется критической. Положение ее в ряде чисел Рейнольдса зависит, что очень важно, от начальной степени турбулентности потока воздуха и шероховатости поверхности цилиндра, с увеличением которых кризис юбтекания наступает раньше (см. рис. 3.8).

Коэффициент лобового сопротивления гладкого круглого цилиндра до кризиса обтекания, не считая области малых чисел Re, принимается многими равными 1,2, по другим данным, он немного более единицы (НАСА — Национальный совещательный комитет по аэронавтике, США).

При числах Re<10 силы вязкости играют преобладающую роль по сравнению с силами давления; здесь поток, окружающий цилиндр, имеет ламинарный характер, а линии тока приближаются к линиям тока в условиях полного обтекания. За цилиндром тянется колеблющаяся струя воздуха (см. рис. 3.11, а), распадающаяся в дальнейшем на отдельные вихри. В области чисел Рейнольдса 2,5·10²5, т. е. до кризиса, движение в пограничном слое ламинарное, а за цилиндром образуется вихреобразная область с пониженным давлением. Отрыв пограничного слоя происходит несколько впереди наибольшего (миделевеого) сечения цилиндра (см. рис. 3.11, б). Давление на цилиндр в этой области чисел Рейнольдса определяется главным образом давлением от разрежения р<р₀ за цилиндром. При дальнейшем увеличении чисел Рейнольдса (Re=1,8·10⁵=3,5·10⁵) происходит кризис: точки Б и В (точнее, линия) отрыва пограничного слоя располагаются за наибольшим сечением (см. рис. 3.11, в). Характер обтекания цилиндра приближается к полному обтеканию, и, несмотря на увеличение сил трения, коэффициент лобового сопротивления цилиндра резко падает, так как область разрежения значительно сузилась. Круглый цилиндр в закритической области как бы приближается к хорошо обтекаемым телам, что весьма важно для проектирования строительных конструкций.

Подобная картина наблюдается у цилиндров квадратного, прямоугольного, треугольного и ромбовидного сечений с радиусом скругления кромок, соизмеримым с характерным размером тела. При числах Рейнольдса около (3÷10)·10⁵ у них наступает, как и у круглого цилиндра, кризис обтекания, коэффициент лобового сопротивления их резко падает, достигает минимума, а затем возрастает значительно быстрее, чем коэффициент сопротивления круглого цилиндра. Кризис наступает тем раньше, чем больше радиус скругления кромок (НАСА).

Скругление острых кромок тел понижает их лобовое сопротивление и до кризиса. Это особенно заметно у прямоугольных цилиндров (призм), большой стороной направленных по потоку.

Сопротивление тела зависит от степени турбулентности потока, потому что с ростом ее ускоряется переход пограничного слоя из ламинарного в турбулентный. Турбулентность сильнее сказывается на сопротивлении хорошо обтекаемых тел, у которых оно определяется по преимуществу формой тела. У круглого цилиндра до кризиса турбулентность может понизить величину коэффициента лобового сопротивления до 50% значения в потоке с малой пульсацией скорости. После кризиса коэффициент с_х незначительно — до 10% — возрастает с ростом степени турбулентности даже до ε=5÷10%.

Влияние турбулентности на плохо обтекаемые пластинки и тела, у которых нет кризиса обтекания, незначительно.

Вообще коэффициент лобового сопротивления цилиндра зависит не только от числа Рейнольдса и шероховатости поверхности, но и от начальной турбулентности потока.

Строителя интересуют нагрузки на сооружения, расположенные на поверхности земли, т. е. в условиях сильной турбулентности. Поэтому может оказаться, что данные исследований моделей в аэродинамической трубе с малой, искусственно сниженной, турбулентностью окажутся в несоответствии с сопротивлением тела в действительных условиях.

Лобовое сопротивление разнообразных по форме тел, например приведенных на рис. 3.5, по старой теории (Ньютона), должно быть одинаковым, поскольку их наветренная площадь равна одной и той же площади круга. По современной гидродинамической теории сопротивления жидкости движущемуся в ней телу, лобовое сопротивление определяется в значительной мере процессами, происходящими позади тела и зависящими в основном от формы его кормовой части. Вот почему при равной наветренной площади сопротивление стойки во много раз меньше сопротивления плоской пластинки (см. рис. 3.5). С увеличением размеров тела по потоку его сопротивление становится меньше, затем оно немного растет вследствие увеличения сил трения.

 
Рис. 3.14. Хорошо обтекаемое тело >

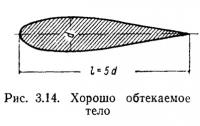
Для создания хорошо обтекаемого тела ему придают такую форму, при которой струи жидкости, обтекающие его снизу и сверху (справа и слева), отрываются на небольшом расстоянии друг от друга, как у тела в виде профильной пластинки с заостренной кормовой частью (рис. 3.14). У такого тела отрыв потока происходит у задней кромки, поэтому область разрежения очень мала. Иначе говоря, происходит почти полное обтекание, и лобовое сопротивление тела в основном определяется силами трения, которые малы. Если у профильной пластинки по рис. 3.14 оставить переднюю притупленную (закругленную) часть, а заднюю (заостренную) отсечь, то ее сопротивление увеличится в десять раз. При отношении ширины к толщине, равном 3, коэффициент лобового сопротивления профильной пластинки, например стойки, равен 0,06—0,08.

Меньшие значения коэффициента относятся к пластинке с более гладкой поверхностью. Еще меньший коэффициент c_x=0,026 будет у веретенообразного тела вращения с передним притупленным концом и задним вытянутым и заостренным.

 
Рис. 3.15. Влияние шероховатости иа коэффициент лобового сопротивления круглого цилиндра >

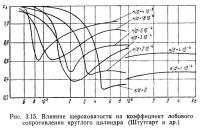
При больших числах Рейнольдса коэффициент лобового сопротивления шероховатых круглых цилиндров больше, чем гладких (рис. 3.15). Критическая область у цилиндра начинается тем раньше, чем больше его шероховатость, поэтому в определенном интервале чисел Re коэффициент сх шероховатого может быть меньше c_x гладкого.

В закризисной области коэффициент лобового сопротивление шероховатого цилиндра растет быстрее и становится в 2—3 раза больше коэффициента сопротивления гладкого цилиндра.

Малая толщина пограничного слоя позволяет влиять на него с помощью небольших по высоте препятствий на пути движения слоя: создавать явную подъемную силу, препятствовать синхронным срывам вихрей по длине цилиндра и др. Таким активным вмешательством в характер обтекания тела можно изменять его поведение в нужном направлении, например для гашения вибрации.

Расположенные на гладкой трубе обстройки, даже малой высоты по сравнению с диаметром трубы, существенно повышают аэродинамическое сопротивление. Такие детали качественно изменяют картину обтекания цилиндра — отрыв пограничного слоя происходит с острых краев деталей. Область пониженного давления расширяется, что приводит к увеличению лобового сопротивления. Обтекание цилиндра становится как бы докризисным.

Строительные конструкции расположены на земле, в непосредственной близости от них часто размещены другие, поэтому учет взаимного влияния обязателен, так как поток будет сильно возмущенным. Профиль скорости у земли зависит от шероховатости ее поверхности, поэтому распределение давления по высоте натуры будет отличаться от условий в аэродинамической трубе. В этой связи размеры (высоту) зерен на поверхности модели делают пропорционально уменьшению характерного размера прототипа. Несоблюдение масштаба шероховатости поверхности земли приводит к существенным ошибкам при суждении о распределении давления по поверхности тела. Ошибка в величине давления в области разрежения может быть до 300%, например у здания с двускатной крышей. Ошибка в давлении на наветренную сторону (стену) этого здания меньше — до 30%,

 
Рис. 3.16. Течение жидкости около цилиндров-тандем >

Изучение объектов строительства проводят на геометрически и аэродинамически подобных моделях, включая моделирование шероховатости и, что не менее важно, учитывая шероховатость поверхности земли вблизи объекта. Важно также выполнять требования одинаковой степени турбулентности потока в аэродинамической трубе и в свободной атмосфере.

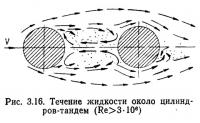
Рассмотрим круглый цилиндр, в аэродинамическом — кильватерном следе которого и параллельно переднему расположен другой цилиндр равного диаметра (рис. 3.16). При расстоянии между цилиндрами до 3d между ними образуется застойная зона интенсивной завихренности. Они как бы объединяются в одно, но более сложное, тело. Давление между ними менее статического, поэтому задний цилиндр стремится притянуться к переднему.

 
Рис. 3.17. Коэффициенты лобового сопротивления цилиндров-тандем >

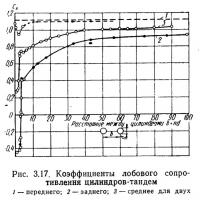
На рис. 3.17 приведены графики коэффициентов лобового сопротивления одинаковых цилиндров-тандем в зависимости от расстояния между ними, выраженного в диаметрах цилиндра. Эти данные относятся к условиям- докризисного обтекания — Re=1,8·10⁵. Как видно на рис. 3.17, при расстоянии между цилиндрами до трех диаметров коэффициент суммарного лобового сопротивления цилиндров-тандем меньше коэффициента сопротивления одного цилиндра. Подобная картина обтекания цилиндров-тандем будет и в за-кризисной области.

Общее лобовое сопротивление не очень далеко расположенных цилиндров-тандем всегда меньше суммы сопротивлений изолированных. При расстоянии даже 90 диаметров лобовое сопротивление обоих цилиндров равно 1,83 одинарного. Лобовое сопротивление шероховатых цилиндров-тандем увеличивается после кризиса, оставаясь все же меньше суммы сопротивлений изолированных цилиндров. Коэффициент лобового сопротивления заднего цилиндра всегда меньше, чем переднего. Небольшая по толщине решетка (связь) между цилиндрами-тандем почти не влияет на величину сопротивления, если относительное расстояние между цилиндрами невелико.

Влияние малого смещения заднего цилиндра с общей оси сказывается на сопротивлении обоих только при небольших расстояниях между ними. Например, при расстоянии, равном одному диаметру, и угле скольжения 10° коэффициент лобового сопротивления увеличивается на 100%, а при расстоянии 4—6 диаметров — всего лишь на 10%. При малом расстоянии между цилиндрами (доли диаметра) и угле скольжения 90° сопротивление двух цилиндров немного больше суммы сопротивления двух изолированных цилиндров.

Кризис сопротивления присущ всем телам, у которых точка отрыва пограничного слоя может перемещаться в зависимости от числа Рейнольдса. Это справедливо при неизменной степени турбулентности потока. Круглый цилиндр, шар, эллипсоид являются примером таких тел. У хорошо обтекаемых тел кризиса сопротивления в указанном смысле не может быть, потому что их сопротивление определяется преимущественно силами трения. Но и здесь переход течения в пограничном слое, например из турбулентного в ламинарный, сильно снижает c_x профиля.

Примечания

1. Н. Е. Кочин, И. А. Кибель, Н. В. Розе. «Теоретическая гидромеханика». Гостехиздат, М,—Л., 1948.

2. При расчете конструкций в условиях воздействия взрывной волны со сжимаемостью необходимо считаться.

3. Положительная разность полного давления и статического (атмосферного).

4. Разброс объясняется, по-видимому, небольшими различиями в моделях.

5. Степенью турбулентности принято считать отношение среднеквадратичного значения пульсационной компоненты продольной скорости к средней скорости, выраженное в процентах.

Источник: «Ветровая нагрузка на сооружения», Г. А. Савицкий, 1972