Ветровая нагрузка на специальные конструкции

Выяснение ветровой нагрузки на специальные виды сооружений, технологические требования к которым сильно влияют на его форму, — задача более сложная. Рассмотрим примеры обтекания простых тел, которые помогут пролить свет на поведение сложных конструкций [18].

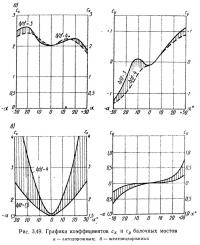
В табл. 3.6 приведены коэффициенты лобового сопротивления различных тел вращения, которые могут быть одним из элементов сложной конструкции. Например, характерно резкое уменьшение коэффициента лобового сопротивления круглого цилиндра, если его торцы закончить полушариями. Поэтому крышу горизонтального резервуара лучше делать сферической, а не плоской. Если открытую шаровую полусферу (см. табл. 3.6) закрыть плоской крышей, то с_х снижается до 1,16; еще лучше, когда крыша сферическая, что приближает сопротивление такого тела к сопротивлению шара. Перфорация настила мостов может снизить опрокидывающий момент и повысить аэродинамическую устойчивость висячего моста.


Обтекатели, широко применяемые в самолетостроении, из-за различного направления ветра не могут, казалось бы, найти применение в строительстве. В действительности, можно применять формы конструкций с меньшим аэродинамическим сопротивлением или ставить обтекатели, понижающие ветровую нагрузку. Например, горизонтальный диск на радиомачте был выполнен в форме метательного диска вместо открытой решетчатой конструкции. Это дало снижение ветровой нагрузки на порядок. Обтекатели на балке жесткости проезжей части висячего моста снижают его ветровую нагрузку. Кольцевые обтекатели, завершающие как бы край параболоида, снижают коэффициент c_R на 15%, если диаметр такого кольца d=0,07D, и на 20% — если d=0,01D, где D — диаметр раскрыва; снижение аэродинамического момента больше на 30 и 60% соответственно.


Обтекателем в своем роде является круглый цилиндр из стеклопластика или другого радиопрозрачного материала, окружающий телевизионные антенны, установленные на решетчатой конструкции, В условиях сильного обледенения такой обтекатель значительно снижает ветровую нагрузку на телевизионную опору и, кроме того, улучшает радиотехнические параметры антенн. Фланцы, ребра, утолщения и шпангоуты ставят с внутренней стороны цилиндра, чтобы не повышать его с_х.

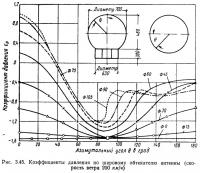
Радиолокаторы и радиотелескопы заключают в жесткие или мягкие шаровые обтекатели из радиопрозрачного материала. Жесткие конструкции выполняют диаметром до 45 м, мягкие — до 65 м. Сопротивление ветру мягких обтекателей вследствие изменения формы при ветре больше, чем сопротивление равновеликого шара. Чаще всего обтекатели выполняют в виде части шаровой сферы, установленной на цилиндре (см. рис. 3.45). Коэффициенты давления по обтекателю получены при Re=3·10⁶, что позволяет считать их достаточно достоверными для натуры, у которой Re=107 и более. При скорости ветра 200 км/ч (55,5 м/сек) коэффициенты для сферы: с_у=0,9 и с_х=0,4, а результирующий с_R≈1,0. Более подробные сведения о ветровой нагрузке на обтекатели и библиографию можно найти в [19].

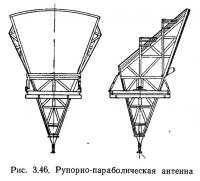
Ветровая нагрузка на сложные по форме конструкции может быть определена приближенно; для этого используют данные о простых телах, так как коэффициенты лобового сопротивления даже существенно отличающихся по форме тел с острыми краями изменяются незначительно по величине (см. табл. 3.1). Например, коэффициент лобового сопротивления сложной по форме конструкции в виде рупорно-параболической антенны (удлинение λ=2) радиорелейных линий (рис. 3.46), определенный опытным путем, равен 1,17—1,2, а как плоской пластинки — 1,2. Коэффициент лобового сопротивления параболической антенны со сплошной отражающей поверхностью по опытам 1,3; среднее между коэффициентами лобового сопротивления чаши в виде полушария и плоского круглого диска — (1,5+1,12):2=1,31, т. е. расчетный коэффициент одинаков с опытными данными.

Центральное отверстие в плоском круглом диске, если оно не превышает 0,6 его диаметра D, мало изменяет характер обтекания и величину коэффициентов лобового сопротивления и подъемной силы диска. С увеличением диаметра отверстия d сопротивление такого диска приближается к сопротивлению кольцевой пластинки. При отношении d/D≈l коэффициент с_х≈2, т. е. он одинаков с с_х бесконечно длинной пластинки.


Коэффициент лобового сопротивления гладких круглых цилиндров с плоскими торцами и осью по потоку с ростом удлинения до 2—3 падает с 1,1 до ОД а затем растет до 0,95, последнее объясняется повышением сопротивления трения. Скругление торцов цилиндра значительно снижает его лобовое сопротивление (см. табл. 3.6). Влияние скругления торцов на сопротивле-нйе цилиндра при расположении его нормально к потоку сказывается тем меньше, чем больше удлинение цилиндра.

Лобовое сопротивление параболического отражателя антенны или гелиоустановки зависит не только от площади раскрыва, но и от его глубины. Его сопротивление находят линейной интерполяцией между значениями коэффициента лобового сопротивления плоского круглого диска, глубина которого равна нулю, и коэффициента сопротивления полушария, глубина которого 0,5.

Для расчета механизмов привода поворачивающихся или вращающихся антенн необходимо знание величины ветровой нагрузки и моментов относительно осей вращения. Для полной оценки прочности конструкции и точности отсчета нужны не только максимальные значения аэродинамических коэффициентов, но и их производные по углам атаки (скольжения), так как резкие изменения аэродинамических коэффициентов при вращении могут вызвать дополнительные деформации антенны. В этой связи необходимы исследования в аэродинамической трубе антенны, вместе с механизмами, опорным устройством и другими элементами.

Общее давление ветра на щит тем меньше, чем больше его размеры. Это позволяет вводить поправочные коэффициенты при определении ветровой нагрузки на конструкции, отличающиеся размерами. Например, во Франции (нормы 1965 г.) при ширине здания или сооружения 100 м этот коэффициент принимают равным 0,7, при 4 м он равен 1,0, а при 1—2 м — 1,2. Учет влияния абсолютных размеров конструкции на их лобовое сопротивление — это скорее статистический подход к расчетному скоростному напору ветра, а не уточнение аэродинамических характе- -ристик, так как сопротивление геометрических подобных тел с острыми краями мало зависит от числа Рейнольдса.


При определении ветровой нагрузки на тела в виде круглого цилиндра, шара, эллипсоида следует помнить, что их лобовое сопротивление существенно возрастает, если на них размещены вдоль образующих даже небольшие по сравнению с их диаметром детали. Простое сложение ветровой нагрузки на основную принимаемую гладкой конструкцию с нагрузкой на эти детали приводит к большой ошибке. При закризисном обтекании коэффициент лобового сопротивления трубы с различными накладками увеличивается до 1,0—1,2 (см. рис. 3.28). Ветровую нагрузку на обстройки учитывают отдельно и суммируют с нагрузкой на трубу. Например, лобовое сопротивление ветру цилиндрической или конической трубы, шаровой емкости будет значительно больше, если на ней устроена лестница. Расположенные на трубе небольшие детали приводят, кроме того, к появлению подъемной силы, которая, суммируясь с лобовым сопротивлением, увеличивает нагрузку и может стать в некоторых случаях причиной регулярных колебаний (см. рис. 3.29) и даже разрушения трубы.

Для различных целей применяют решетки, ветровая нагрузка на которые является основной. Например, отражающие поверхности радиолокаторов (радаров), радиотелескопов, антенн для космической связи и радионавигации для снижения ветровой нагрузки на них, если это возможно по технологическим соображениям, выполняют решетчатыми. Знаки речной и прибрежной навигации в виде решетчатых щитов — другой пример.

Решетки могут быть с различным заполнением (сплошностью) и из разного профиля стержней (круг, прямоугольник, квадрат и другие сечения). К решеткам часто относят перфорированные пластины. Вообще, коэффициент лобового сопротивления решеток не связан линейно с коэффициентом заполнения: ветровая нагрузка на него снижается медленнее роста сквозности пластинки.

Коэффициенты лобового сопротивления плоских решеток из прямоугольного сечения пластин со скошенными краями — фасками (Геттинген):


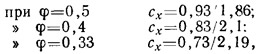
решеток из прямоугольных пластин без фасок:



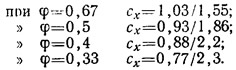
В числителе приведены значения коэффициента с_х решетки, отнесенные к площади щита по наружным обводам, в знаменателе — к суммарной площади всех пластин.

Для проверки прочности при кручении и несущей способности поддерживающей решетку конструкции необходимо знание боковой силы. Наибольшее значение ее у решеток будет при угле скольжения (β=60÷70°, оно равно приблизительно 0,15 лобового сопротивления. Это значение коэффициента боковой силы примерно одинаково при любом коэффициенте заполнения решетки.

Коэффициент лобового сопротивления решетки из круглых стержней или проволоки принимают 0,67 сопротивления решетки из пластин без фасок. Характерно, что сопротивление решетки, отнесенное к теневой площади всех пластин, понижается с увеличением коэффициента заполнения. В среднем коэффициент лобового сопротивления решетки из пластин можно принять равным коэффициенту сопротивления длинной пластинки; ошибка возрастает с увеличением коэффициента заполнения. Фаски у пластин немного снижают сопротивление решетки.

Коэффициенты лобового сопротивления решетки из перекрещивающихся полос, круглых стержней, проволоки или в виде перфорированных пластин зависят от степени заполнения. Например, коэффициент с_х перфорированной квадратной пластины при φ= 0,2 равен 1,65, при φ=0,28 равен 1,5. При увеличении значения φ он в пределе равен сопротивлению сплошной пластины. Коэффициент лобового сопротивления решетки, выполненной из перекрещивающихся круглых стержней, при φ=0,56 и обтекании до кризиса равен 1,0. Характерно, что наибольшее сопротивление потоку будет при действии его по нормали, в отличие От сопротивления сплошной пластинки, у которой наибольшее значение, равное 1,4—1,5 лобового сопротивления, оказывается в окрестности угла β=40°. Величина коэффициента тангенциальной боковой силы решетчатой пластинки обычно не более 0,3 коэффициента лобового сопротивления при α=90°.


Во многих радиотехнических устройствах наряду с плоскими решетками применяют конструкции в виде параболоида вращения или параболического цилиндра со сплошной или решетчатой отражающей поверхностью. Ниже приводятся опытные аэродинамические коэффициенты параболического радиотелескопа диаметром 25 м, установленного в Боннской обсерватории (ФРГ). Отражающая поверхность его выполнена из перфорированных листов с размером ячеек 10X10 мм2, толщина перегородок 2 мм, коэффициент заполнения 0,4. Коэффициент лобового сопротивления при действии ветра нормально к плоскости раскрыва 0,695, с тыльной (противоположной) стороны 0,676, при ветре, параллельном плоскости: c_x=0,131; с_у=0,031; c_m=0,0192. При угле атаки 45° к плоскости c_x=0,459 и 0,498; c_y=0,120 и —0,166; c_m=0,035 и 0,016; здесь первые цифры относятся к действию ветра с тыльной стороны, а вторые — с лицевой. Эти коэффициенты отнесены к площади раскрыва радиотелескопа, равной 491 м². Если коэффициент лобового сопротивления отнести к проекции теневой площади всех стержней решетки (за вычетом отверстий в листах), то он будет 1,69—1,74, т. е. будет равен коэффициенту лобового сопротивления решетчатой фермы с большим заполнением (см. рис. 3.32). В действительности, коэффициент заполнения немного больше, если учесть кривизну отражающей поверхности.

Расчетная ветровая нагрузка на параболические или подобные типы антенн может быть в 1,4 раза больше, чем при лобовом ветре. Это будет при углах атаки 30—40°. Кроме того, при положении оси вращения в горизонтальной плоскости не на оси нулевых аэродинамических моментов возникает пульсирующий за оборот крутящий момент, величина которого зависит от направления и скорости ветра, а также от скорости вращения антенны. В параболических антеннах ось нулевых моментов расположена от вершины параболы на расстоянии 0,1—0,2 диаметра в сторону излучения.

Для вращающихся антенн-локаторов большое значение имеет величина аэродинамического. момента, определяющая мощность приводов вращения. Оптимальные моменты относительно осей y и z достигаются выбором положения оси вращения антенны, которое определяется по материалам исследования моделей в трубе.

В стационарных условиях, т. е. без вращения антенны, наибольшее значение момента получается в окрестности углов 70 и 130°. Для сглаживания пиков моментов, неблагоприятно отражающихся на точности отсчетов, применяют закрылки-стабилизаторы. Это делают, несмотря на увеличение коэффициентов с_х и с_у; последний может возрасти в 2 раза и даже изменить свой знак. Радикальным решением является выдвижение оси вращения в направлении излучения антенны, что совместно с действием закрылок снижает аэродинамический момент в 2 раза и более.

Установка на параболической антенне козырьков-обтекателей снижает ее лобовое сопротивление на 10—20%. Заметное действие козырьков сказывается при радиусе закруглений, соизмеримом с диаметром параболы.

Статические аэродинамические моменты параболических антенн (полных или усеченных) мало зависят от числа Рейнольдса, что упрощает моделирование.

Основное влияние на величину и характер зависимости аэродинамических коэффициентов антенны от угла атаки (поворота) имеют скорость вращения п и скорость ветра V, или, иначе говоря, число Струхаля:


где L — наибольший размер антенны, например диаметр параболы или длина усеченного параболоида.

Для постоянно вращающихся антенн существенное значение имеет, кроме того, снижение величины среднеквадратичного момента, которым определяется мощность привода.

Неравномерность вращения антенны за оборот вносит ошибки в отсчеты ее местоположения, которые увеличиваются с ростом пиков моментов. Поправки к отсчету могут быть учтены, если известны аэродинамические характеристики антенны в функции углов поворота. При моделировании чаще всего ограничиваются подобием, определяемым числом Струхаля, полагая, не без основания, пренебрежимо малую зависимость аэродинамических коэффициентов от числа Рейнольдса.

Вращение антенны вызывает значительное изменение формы кривой момента М_α в функции угла поворота. В графике М=f(α) появляются четыре пика (при углах α=60; 130; 250 и 300—320°) вместо двух в стационарных условиях, т .е. при n=0. С ростом числа Струхаля среднеквадратичное значение момента повышается.

У параболических антенн с решетчатым отражателем вращение вызывает меньшие искажения графиков аэродинамических моментов, записанных у неподвижных антенн, чем со сплошным отражателем. Аэродинамический момент решетчатого параболоида в статическом режиме меньше, чем у сплошного одинаковых размеров. В динамическом режиме преимущество решетчатых конструкций отражателя может и не обнаружиться. Снижение пиков моментов при выдвижении вперед оси вращения сказывается больше у антенн с решетчатыми отражателями.

Расчет подъемных кранов на ветровую нагрузку ведется в соответствии с ГОСТ 1451—65 [8]. На судовые и плавучие краны стандарт не распространяется. Особенностью стандарта являются два расчетных состояния кранов: нерабочее и рабочее. В первом состоянии ветровую нагрузку определяют по СНиП. В рабочем состоянии скоростной напор принимается независимо от района установки крана равным 15 кГ/м². В особых случаях он может быть повышен до 25 кГ/м². Наряду с наиболее распространенными приемами определения ветровой нагрузки в этом ГОСТе предложены значительно более сложные формулы для вычисления аэродинамических коэффициентов. В них учитываются, например, отдельно теневые площади поясов и решетки, отношение коэффициентов сопротивлений при действии ветра вдоль и поперек фермы.

В стандарте на подъемные краны в отличие от наиболее распространенной характеристики решетчатых конструкций в виде коэффициента заполнения фигурирует аналогичная ей зависимость в форме отношения поперечного размера пояса фермы к ее ширине. Для плоской фермы оперируют с коэффициентом заполнения, при изменении которого сумму произведений коэффициентов лобового сопротивления стержней фермы на их теневую площадь [формула (3.15)] умножают на поправочный коэффициент, равный 0,92 при φ=0,1; 0,81 при φ=0,2; 0,75 при φ=0,3÷0,9. Этим коэффициентом учитывают взаимное аэродинамическое влияние стержней фермы. Коэффициент лобового сопротивления фасонок фермы принимают равным 1,2.

Коэффициенты лобового сопротивления элементов фермы принимают с учетом их удлинения и направления ветра. Величину лобового сопротивления стержней из труб и круглой стали определяют в зависимости от значения Vd, являющегося модификацией числа Рейнольдса,

При косом ветре на круглые цилиндры (трубы, канаты) скорость потока в числе Рейнольдса определяется с учетом угла между их осью и направлением потока. Коэффициент сопротивления цилиндра для нагрузки, нормальной к оси (хорде), считают пропорциональным sin²β, а в направлении потока — пропорционально sin³β.

Значение коэффициентов лобового сопротивления стержней с острыми краями в решетчатых конструкциях в этом ГОСТе значительно больше, чем 1,4, рекомендуемый СНиП. Коэффициент лобового сопротивления крановой кабины по этому ГОСТу 1,2. Ветровая нагрузка на груз принимается в зависимости от грузоподъемности крана.

Проектирование высоковольтных линий передачи электрической энергии ведется в соответствии с «Правилами устройства электроустановок» (ПУЭ), в которых имеется раздел о ветровой нагрузке на провода и защитные тросы [20]. Расчет опор высоковольтных линий, включая и определение ветровой нагрузки на конструкции, производится по СНиП II-И.9-62.

Ветровая нагрузка на провод или защитный трос, нормальная к его оси, определяется по формуле


где q — скоростной напор ветра;
α — коэффициент, учитывающий неравномерность скорости ветра по пролету провода или троса, принимаемый равным 1,0 при q=27 кГ/м²; 0,85 при q=40 кГ/м²; 0,75 при q=55 кГ/м² и 0,7 при q>75 кГ/м²;
с_х — коэффициент лобового сопротивления, равный 1,2 при диаметре провода или троса d≤20 мм и 1,1 при d>20 мм (см. рис. 3.30);
l и φ — длина провода и угол между направлением ветра и хордой провода или троса.

Коэффициент лобового сопротивления обледенелого провода при действии ветра вдоль большой оси сечения (отношение осей 5:3), по материалам опытов, в трубе 0,5—0,6, поперек — около 1.0 (ГДР).

Это позволяет снижать ветровую нагрузку на провода и тросы, следовательно, и на опоры, если коэффициент с_х считать пропорциональным sin³φ, а коэффициент с_х обледенелых проводов принять около 0,7.

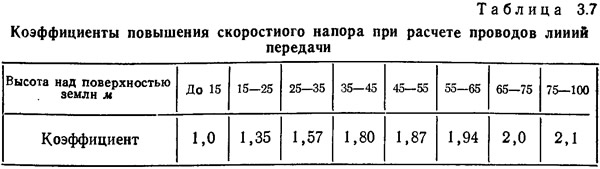
При определении ветровой нагрузки на провода или тросы вводятся коэффициенты увеличения скоростного напора ветра с высотой по табл. 3.7.


Ветровая нагрузка на промышленное оборудование колонного типа и. этажерки, установленные на открытом воздухе, определяется в соответствии со специальными Указаниями [9], являющимися дополнением к СНиП «Ветровые нагрузки» [2].

Согласно Указаниям для ряда параллельных балок, ригелей, ребер, плит и пр. аэродинамические коэффициенты¹ принимаются для первой балки с_х=1,4, для второй и последующих балок


где η₁ — коэффициент, определяемый по табл. 3.8.


Аэродинамический коэффициент круглого цилиндра с плоскими торцами при действии ветра вдоль его оси с_х=1.

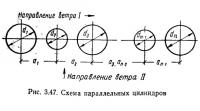
Аэродинамический коэффициент для первого круглого цилиндра, стоящего впереди в ряду параллельных цилиндров разных диаметров и с различными расстояниями а между их осями (рис. 3.47), принимается по рис. 3.25. Для второго цилиндра по потоку и последующих коэффициент с_х определяется по формуле


где с_х — коэффициент лобового сопротивления первого цилиндра по рис. 3.25;
η₂ — коэффициент по табл. 3.9.

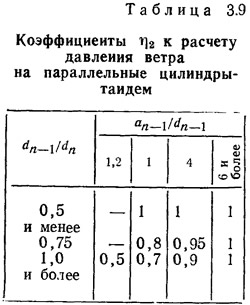
Для случая, когда d_n—1<d_n<d_n—2, коэффициент η₂ для n-го цилиндра принимается как меньшее значение из двух, определенных в зависимости от a_n—1/d_n—1 и (a_n—2+a_n—1)/d_n—2. Для промежуточных значений d_n—1/d_n и a_n—1/d_n—1 коэффициент η₂ определяется линейной интерполяцией.

При направлении ветра перпендикулярно оси ряда параллельных круглых цилиндров аэродинамический коэффициент каждого цилиндра


где с_х — принимается по рис. 3.25;
η₃ — берется по табл. 3.10.


Для случая a_n—1/d_ср≠a_n/d_ср коэффициент η₃ для n-го цилиндра принимается как большее значение из двух, определенных в зависимости от a_n—1/d_ср и a_n/d_ср.

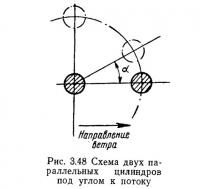
Для цилиндров или трубопроводов, расположенных параллельно (рис. 3.48), при различном направлении ветра аэродинамические коэффициенты определяются:

• для углов 0°≤α<30° — как это сказано выше, т. е. как для цилиндров при направлении ветра / (см. рис. 3.47);
• для углов 75°<α<90° — как для цилиндров при направлении ветра 11 (рис. 3.47);
• для углов 30°≤α≤75° — как для одиночных цилиндров.

Коэффициент лобового сопротивления труб с надстройками — негладких — определяют с учетом данных, помещенных ранее в тексте.

Ветровой нагрузке на мосты посвящен ряд работ. Особенно большие по объему исследования за последнее время проводились на моделях висячих мостов, толчком к чему явилась катастрофа Такомского моста (США) в 1940 г. Ветер был причиной разрушения и других мостов больших пролетов.

Ветровая нагрузка на дорожные и городские мосты определяется в соответствии с «Техническими условиями проектирования» [7].

По этим Условиям ветровая нагрузка на мосты относится к прочим временным нагрузкам и воздействиям. Нормативная горизонтальная поперечная ветровая нагрузка на единицу расчетной поверхности равна: а) при подвижной вертикальной нагрузке на мосту: для железных дорог 100 кГ/м², для автомобильных и городских дорог 50 кГ/м²; б) без подвижной нагрузки на мосту для железных дорог 180 кГ/м², для деревянных автодорожных и городских мостов 80 кГ/м², в) при особых сочетаниях нагрузок, включая и монтаж, 50 кГ/м².

В величине ветровых нагрузок учтен коэффициент лобового сопротивления, равный 1,4.

Расчетная ветровая поверхность принимается:

1) для конструкций — равной площади проекции сооружения по наружным обводам на вертикальную плоскость, перпендикулярную направлению ветра, со следующими коэффициентами для сквозных балочных ферм: при двух фермах 0,4, при трех и более фермах 0,5, для площади сквозных арочных ферм между поясами и для сквозных опор 0,5; для площади арочных ферм между нижним поясом и затяжкой или между верхним поясом и проездом, а также для сквозных надарочных строений 0,2, для сплошных пролетных строений, сплошных и деревянных опор, а также для элементов проезжей части 1,0, для перил 0,3—0,8;

2) для железнодорожного подвижного состава — в виде сплошной полосы высотой 3 м с центром давления на высоте 2 м от головки рельса; для колонн автомобилей и других транспортных единиц не учитывается.

Ветровая нагрузка по длине пролета моста считается равномерной. Расчетная ветровая поверхность проезжей части равна ее полной боковой поверхности.

Нормативная продольная горизонтальная ветровая нагрузка на сквозные пролетные строения и опоры учитывается в размере 0,6 нормативной поперечной ветровой нагрузки на главные фермы.

Горизонтальное усилие от продольной ветровой нагрузки на пролетное строение передается на опоры таким же образом, как и усилие от торможения или силы тяги. При этом ветровая нагрузка на сплошные пролетные строения, проезжую часть и подвижной состав не учитывается.

Этим нормативом устанавливаются следующие коэффициенты перегрузки при действии: основных нагрузок 1,5, дополнительных 1,2 и особых 1,0.

Исследования ветровой нагрузки на мосты чаще всего проводятся на моделях, имитирующих секцию моста; моделирование полностью моста делается значительно реже. Натурные наблюдения за поведением мостов при ветре были проведены за последнее время на ряде висячих мостов. Главная цель этих работ состояла в выяснении картины колебаний мостов при ветре, в результате чего выявилась необходимость усиления некоторых мостов. Например, один из самых больших мостов мира — висячий мост через пролив «Золотые ворота» в Сан-Франциско — пришлось усилить, что обошлось очень дорого.

Для выяснения ветровой нагрузки на дорожные мосты были проведены обширные исследования [21; 22; 23], по результатам которых можно сделать некоторые выводы, хотя модели были определенных, наиболее распространенных в каждой стране типов и конструкций мостов.

Влияние коэффициента заполнения и расстояния между фермами на лобовое сопротивление главных ферм мостов имеет одинаковый характер с сопротивлением решетчатых ферм при угле атаки α=0°. При углах α≠0° выявляется большое значение настила моста, повышающего нагрузку и опрокидывающий момент. Сквозные настилы проезжей части моста влияют не меньше, чем сплошные. При косом ветре мосты и две параллельные фермы ведут себя примерно одинаково (см. рис. 3.39).

При углах атаки ±20° лобовое сопротивление моста увеличивается в 1,2 раза, что объясняется влиянием балочной клетки, тем большим, чем шире мост. Основная ветровая нагрузка на мост определяется нагрузкой на главные фермы. Проезжая часть автодорожного моста оказывает большее влияние на общую нагрузку, чем сквозное полотно железнодорожного моста. При углах атаки 15—20° доля нагрузки проезжей части составляет 0,2 общей горизонтальной нагрузки на мост. Поэтому ветровая нагрузка на сплошностенчатые балочные мосты должна определяться при углах атаки α≠ 0°; при угле α=30° эта нагрузка может стать даже больше суммы нагрузок на две одинарные балки. Лобовое сопротивление двух параллельных двутавровых балок без настила и связей даже при расстоянии между ними в несколько высот балки d не достигает двойной величины нагрузки на одну балку (см. рис. 3.35). Коэффициент с_х принимают с учетом данных рис. 3.35.

Коэффициент лобового сопротивления однопутного железнодорожного моста с двумя балками и открытым (с проемами) настилом при отношении ширины к высоте b/d=4; 2 и 1,35 и угле атаки α=20° равен соответственно 2,25; 2,50 и 2,45; при угле α=0° коэффициент с_х=1,5—1,6. Коэффициент лобового сопротивления подобной конструкции автодорожного моста, т. е. со сплошным настилом и отношением b/d=4, при угле α=20° увеличивается в 1,2 раза; коэффициент подъемной силы становится равным 0,75, а при угле α=—20° коэффициент с_у=1.

Коэффициент лобового сопротивления трех параллельных балок двухпутного железнодорожного моста при угле α=20° становится 2,9 (при α=0° он равен 1,5), при угле α=+30° коэффициент с_x=4,75, с_у=0,6.

Характерно, что при отклонении ветра от горизонтального направления нагрузка на балочные мосты со сплошным настилом повышается меньше, чем у железнодорожных со сквозной проезжей частью.

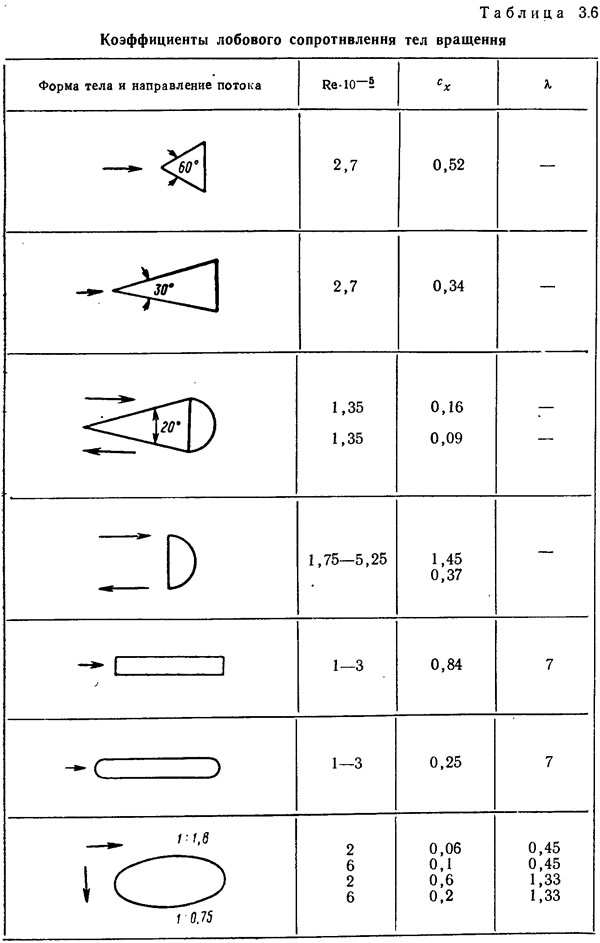
На рис. 3.49 приведены графики аэродинамических коэффициентов c_x и c_y балочных мостов в зависимости от угла атаки. При увеличении угла а коэффициент с_х мостов со сквозным настилом (железнодорожных) растет быстрее, в то время как у мостов со сплошным настилом (автодорожных) с_x немного увеличивается и только до углов атаки 15—20°. Поведение коэффициента c_y .противоположное: сплошной настил способствует более резкому увеличению коэффициента подъемной силы с ростом угла α, кроме того, c_y по величине значительно больше, чем у мостов со сквозным настилом.

Верхние значения коэффициента с_х по заштрихованной области рис. 3.49, б Относятся к мостам с расстоянием между балками 4d, а нижние — к b/d=1,5. При углах атаки 20° коэффициент сх места со сквозным настилом становится в среднем в 1,8 раза больше сопротивления при угле α=0°. Это справедливо при двух и трех главных балках. При угле α=30° коэффициент с_х моста с тремя балками становится больше чем в три раза коэффициента одинарной балки при α=0°.

Лобовое сопротивление автодорожного моста растет с увеличением угла атаки до 20°, после чего оно немного падает. Сквозность настила яяияет на повышение коэффициента сх моста тем сильнее, чем больше расстояние между главными балками.

Нахождение поезда на решетчатом железнодорожном мосту сказывается в увеличении горизонтальной нагрузки. Опрокидывающий момент одно- и двухпутного моста с поездом изменяется мало по сравнению с моментом без поезда на них.

Ветровую нагрузку на мосты больших пролетов, и тем более уникальные по своим размерам или конструкции, определяют по результатам исследований моделей проектируемого моста. Не менее важно правильно назначить величину скоростного напора ветра, который может быть значительно больше наблюдаемого на ближайшей к мосту метеорологической станции, расположенной часто в местности, отличающейся по своему характеру от места предполагаемого строительства моста. Это может сказаться и в большом отклонении ветра от горизонтального направления — до 20° и более. Влияние характера местности и величины скоростного напора сильнее отражается на висячих мостах, особенно больших пролетов.

Данные о железнодорожных и автодорожных мостах могут быть использованы при проектировании эстакад, наклонных мостов, перегружателей и подобных конструкций.

Примечания

1. Здесь под аэродинамическим коэффициентом понимается коэффициент лобового сопротивления.