Ветровая нагрузка на решетчатые конструкции

Для определения ветровой нагрузки на решетчатые конструкции можно воспользоваться материалами, изложенными в СНиП. Для поиска оптимального в смысле ветровой нагрузки решения конструкции, что особенно важно для высоких сооружений, привлекают дополнительные сведения из экспериментальной аэродинамики.

Решетчатые конструкции, как объект действия на них ветровой нагрузки, характеризуются: размерами, удлинением, числом и взаимным расположением ферм, формой сечения и размерами стержней, видами узловых сопряжений стержней, количеством стержней в одном узле, коэффициентом заполнения (сплошности):


где s_j — наветренная площадь стержня и узловых соединений;
S — площадь фермы по наружным обводам.

Гибкость стержня, или, что ближе к аэродинамике, относительное удлинение его в пределах каждой панели, т. е. отношение его геометрической длины между узлами к поперечному размеру, отражается на величине коэффициента лобового сопротивления.

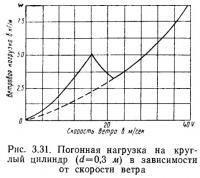
Оптимальной формой сечения стержней строительной конструкции являются труба и круглый стержень, диаметр которых выбран таким, чтобы при расчетной скорости ветра происходило закризисное обтекание, т. е. при наименьшем коэффициенте лобового сопротивления (см. рис. 3.8). Это важно в случае применения шероховатых стержней, например элементов из сборного железобетона (см. рис. 3.15). В качестве примера на рис. 3.31 приведен график ветровой нагрузки на круглый цилиндр диаметром 0,3 м в зависимости от скорости ветра. На рисунке видно, что при скорости, равной 16 м/сек, нагрузка на цилиндр больше, чем при скорости 21 м/сек.

Ветровая нагрузка на трубу диаметром 150 мм в условиях закризисного обтекания и равновеликий по теневой площади угольник 150X150 мм², если следовать указаниям СНиП, будет отличаться в три раза, так как их коэффициенты лобового сопротивления с_х соответственно 0,45 и 1,4. В действительности, наибольшее значение c_R угольника может быть до 2,76 (см. табл. 3.1), т. е. это отношение равно 6. Кроме того, гибкость трубчатого стержня равной длины примерно в два раза меньше, что позволяет полнее использовать материал. Сказанное наглядно демонстрирует преимущества трубчатых стержней в решетчатых конструкциях. Например, вес стальных решетчатых радиомачт и башен из стальных труб в 2—2,5 раза меньше веса конструкций из угольников; то же наблюдается в других областях строительства.


Одним из основных принципов проектирования решетчатых конструкций является концентрация усилий в меньшем числе стержней, т. е. увеличение размеров панелей. Той же цели служит применение стержней предельной допустимой нормами гибкости. В стальных конструкциях стержни поясов и опорных раскосов часто выбирают с гибкостью 80—100, в элементах решетки — до 150, в связях — до 200. За рубежом гибкость сжатых стержней допускают и больше. В высоких сооружениях получили распространение конструкции с раскосами и связями, гибкость которых 350; в предварительно напряженных конструкциях гибкость растянутых элементов не ограничивается. В решетчатых конструкциях из низколегированной стали и тем более из алюминиевых сплавов гибкость стержней принимают не более 40—60. Удлинение разнообразных стержней будет 15—50, если поперечный размер стержня принять в три раза больше радиуса инерции стержня. При таком удлинении стержней с острыми краями их коэффициент лобового сопротивления будет 1,35—1,75 вместо 1,98—2,12 бесконечно длинной пластинки. В СНиП коэффициент лобового сопротивления многих профилей решетчатых конструкций принят 1,4.

Для круглых стержней необходимо считаться с шероховатостью, за которую принимают не начальную, а ту, которая будет у стержня после ряда лет эксплуатации, учитывая при этом специальные меры по поддержанию качества поверхности. Для стальных решетчатых конструкций, оцинкованных или периодически окрашиваемых, относительную шероховатость круглых стержней можно принять 2·10^—4; для алюминиевых, не имеющих часто антикоррозионного покрытия, —1·10^—4; для бетонных конструкций — до 3·10^—3.

Размеры зерен шероховатости или волнистости поверхности зависят от способа производства, поэтому, строго говоря, чем меньше диаметр трубы или круглого стержня, тем больше его относительная шероховатость. У железобетонных конструкций большое значение имеет качество опалубки и способ изготовления сборных элементов. В местностях, где наблюдаются частые переходы температуры воздуха через ноль градусов, разрушение поверхности бетона происходит быстрее, чем в районах с континентальным климатом. С этим необходимо считаться при установлении относительной шероховатости поверхности, которая будет хотя бы к половине намеченного срока службы сооружения и, конечно, больше, чем начальная.


Нагрузка от единичного скоростного напора на плоскую решетчатую ферму, выполненную из разнообразных по профилю стержней и различного удлинения (гибкости), суммируется из нагрузки на каждый элемент площадью s_j с присущим ему аэродинамическим коэффициентом лобового сопротивления с_хj:


Тогда коэффициент лобового сопротивления всей фермы, отнесенный к сумме наветренных площадей стержней,


а отнесенный к площади фермы по наружным обводам, т. е. в свету,


Обращают внимание на то, к какой площади относится аэродинамический коэффициент, помня, что ∑s_j=φS.

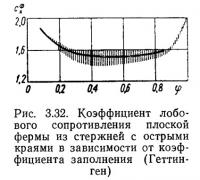
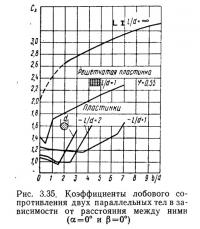
Взаимное расположение стержней в решетчатых конструкциях отражается на величине ветровой нагрузки. Для плоских ферм имеет значение расстояние между ее элементами. Опыты с двумя одинаковыми круглыми цилиндрами, расположенными в одной плоскости, нормальной к потоку, и параллельно друг другу, показали: при расстоянии в свету 0,08d? коэффициент с_х=1,5, при расстоянии d с_х=1,3, а при расстоянии 3d с_х=1,2, т. е. сопротивление каждого по мере удаления друг от друга приближается к сопротивлению изолированного цилиндра до кризиса. Результаты опытов свидетельствуют о быстром затухании взаимного влияния смежных стержней, расположенных в одной плоскости, перпендикулярной потоку, поэтому при малой величине коэффициента заполнения фермы нагрузка на нее приближается к сумме нагрузок на отдельные стержни. При коэффициенте заполнения φ=0,85 и более или φ=0,25 и менее суммарная нагрузка на ферму на 5—15% будет больше, приближаясь к нагрузке на изолированные стержни бесконечной длины (рис. 3.32). Эти данные относятся к бесконечно длинной ферме, выполненной из стержней с острыми краями (см. табл. 3.1). Для ориентировочных расчетов эти значения умножают на 0,75 или 0,67, если ферма выполнена из небольшого диаметра труб или круглой стали. Более точно ветровую нагрузку на ферму вычисляют по формуле (3.15), т. е. по действительным коэффициентам лобового сопротивления шероховатых круглых цилиндров, определенным с учетом чисел Рейнольдса. Разброс (заштрихованная область) на рис. 3.32 вызван разным типом ферм.

Опытные значения коэффициента лобового сопротивления плоских ферм из круглой стали с коэффициентами заполнения 0,18—0,25 и при обтекании до кризиса (число Рейнольдса 1,2·10⁵) находятся в области 0,95—1,05 [18].


Влияние удлинения фермы на лобовое сопротивление заметно сказывается при коэффициенте заполнения φ=0,90÷0,95. При φ=0,25÷0,70, что наиболее часто у стальных конструкций промышленных сооружений и мостов, сопротивление фермы с удлинением 5—10 составляет 0,9 сопротивления бесконечно длинной фермы одинаковой конструкции.

За последнее время наблюдается тенденция к применению решетчатых стальных конструкций с большими размерами панели. Коэффициент лобового сопротивления таких — нового типа — ферм будет выше, чем ферм прежнего типа, т. е. с частой решеткой, материалами исследований которых иногда пользуются в расчетах.

Количество стержней и вид соединений в узлах решетчатых конструкций мало влияет на величину коэффициентов сопротивления — ветровой нагрузки. Влияние деталей сопряжения стержней фермы учитывают конструктивным коэффициентом или, что лучше, наветренную площадь узловых соединений суммируют с площадью стержней.

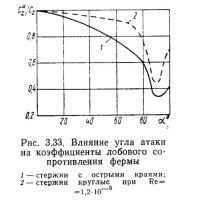
При действии ветра на ферму под углом к ее плоскости нагрузка на нее сначала снижается медленно с ростом угла атаки а (рис. 3.33), что объясняется небольшим сокращением проекции наветренной площади стержней. Начиная с углов α=70÷80°, нагрузка на ферму уменьшается быстро, что вызывается увеличением затенения задних стержней передними по потоку. Минимальное значение нагрузки на плоскую ферму, расположенную под углом к потоку, составляет 0,35—0,45 нагрузки при действии потока нормально к плоскости фермы. Большие величины коэффициентов относятся к фермам из круглых стержней.

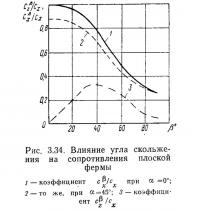
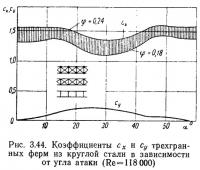
При действии потока под углом скольжения β нагрузка на конструкцию в направлении ветра (лобовое сопротивление) сначала медленно снижается с ростом угла β до 30—40° (рис. 3.34). С дальнейшим увеличением угла β происходит более быстрое снижение коэффициентов сопротивления до 0,25 лобового сопротивления при β=0°.

Коэффициент боковой силы, действующей в направлении оси z на плоскую ферму, при углах атаки α=0 и 45° сначала повышается; при угле скольжения β=30÷45° достигает максимума, равного примерно 0,35 лобового сопротивления, затем понижается и при β=90° становится равным 0,15—0,2 лобового сопротивления при углах α=0° и β=0°. При α=90° коэффициент c_z=0,1с_х. Коэффициенты с_х и c_z на рис. 3.33 и рис. 3.34 отнесены к постоянной наветренной площади фермы, за которую принята сумма проекций площадей стержней и узловых деталей на нормальную к потоку плоскость.


При углах атаки α≠0° и скольжения (β≠0° лобовое сопротивление фермы уменьшается; оно может быть определено умножением на поправочные коэффициенты, взятые по рис. 3.33 и 3.34. Это, строго говоря, приближенно, так как геометрическое сложение сил сопротивления по двум направлениям не отражает действительной картины из-за разных условий обтекания.

В исследованиях ветровой нагрузки на пространственные конструкции наибольшее внимание было уделено двум одинаковым плоским фермам, расположенным в параллельных плоскостях, башням и мачтам преимущественно треугольного и квадратного сечений.

Из общих физических представлений следует, что ветровая нагрузка на заднее по потоку тело всегда меньше, чем на переднее. Нагрузка на расположенные в двух параллельных плоскостях пластинки зависит от расстояния между ними (рис. 3.35). Влияние передней по потоку пластинки на заднюю заметно проявляется при расстояниях между ними до 2—3 высот (диаметров), т. е. в области, наиболее интересной для строителя.

Визуализацией течения жидкости установлено, что завихренная область за телом распространяется в стороны от оси симметрии, направленной по потоку, на относительно небольшую величину, в то время как по потоку — на большое расстояние. Поэтому наибольшая нагрузка на две фермы будет при направлении ветра под небольшим углом скольжения, когда стержни задней но потоку фермы выйдут из тени передней.

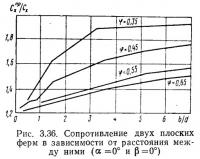
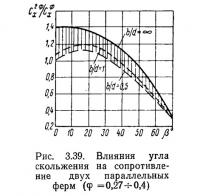
Наиболее интересно поведение ферм при относительно небольших расстояниях между ними — до 2—3 d, где d — высота фермы, и при коэффициентах заполнения фермы 0,15—0,6, распространенных в строительных конструкциях. Нагрузка на две параллельные фермы будет тем больше, чем дальше они расположены друг от друга и чем меньше их коэффициент заполнения (рис. 3.36). Графики построены для безразмерного коэффициента лобового сопротивления, поскольку таким путем удается лучше учесть особенности ферм, например удлинение фермы, форму сечения стержней и, что особенно важно, разную величину коэффициента лобового сопротивления одинарной фермы, принимаемого за исходный. В пределе при отношении b/d=∞ (b — расстояние между фермами) лобовое сопротивление двух решетчатых ферм равно удвоенной величине сопротивления одинарной фермы.

Коэффициент лобового сопротивления двух ферм можно представить в виде



где с^ф_х — коэффициент лобового сопротивления плоской фермы;
η — отношение лобового сопротивления подветренной фермы к сопротивлению наветренной.

Коэффициент с^ф_х принимают по рис. 3.32, но с поправкой на удлинение, или определяют по формуле (3.16), а коэффициент влияния задней фермы 1+η — по рис. 3.36.

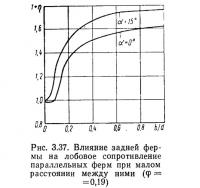
Интересно знание ветровой нагрузки на две плоские фермы при расстоянии между ними в долях высоты фермы d (рис. 3.37). Существенное увеличение нагрузки на ферму заметно при углах атаки 10—20°. При расстоянии между фермами до 0,06 d нагрузка на обе фермы становится меньше, чем на одну. Последний случай представляет, скорее, теоретический интерес, но вместе с тем указывает на малое влияние различных дополнительных элементов, установленных вблизи элементов фермы.

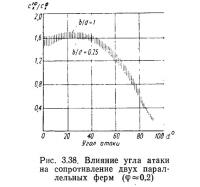
Нагрузка на пространственную решетчатую конструкцию из двух параллельных ферм при действии ветра под небольшим углом атаки к плоскости передней фермы немного увеличивается, поскольку стержни задней по потоку фермы выходят из аэродинамической тени передней. С ростом угла атаки нагрузка на конструкцию падает сначала медленно, а затем быстро (рис. 3.38). Это объясняется все большим затенением задних ферм передними. При угле атаки α≈90° суммарная ветровая нагрузка на две фермы определяется в основном нагрузкой на пояса обеих ферм.

При действии ветра под углом к плоскости симметрии пространственной конструкции из двух параллельных ферм нагрузка на нее сначала увеличивается с ростом угла скольжения β (рис. 3.39), потому что при малых углах стержни задней фермы выходят из тени передних. При углах β=20÷30° нагрузка на конструкцию достигает наибольшего значения. С увеличением расстояния между фермами нагрузка на обе растет все меньше. При бесконечно большом расстоянии между фермами характер изменения нагрузки в зависимости от угла скольжения приближается к графику сопротивления изолированной (одинарной) фермы. При отношении b/d≥1,5 рост нагрузки становится уже малым и зависимость ее с увеличением угла β все более приближается к случаю, когда b/d=∞. Влияние коэффициента заполнения фермы в пределах 0,25—0,4 проявляется в повышении нагрузки; характер ее зависимости от угла β остается примерно одинаковым. При угле β=70° нагрузка на две фермы составляет приблизительно 0,25 наибольшей величины нагрузки; с дальнейшим ростом угла β она изменяется мало.

Анализ действия ветра на фермы при изменении углов атаки и скольжения позволяет сделать следующее заключение: наибольшая нагрузка на фермы будет при действии ветра, направленного под углом к горизонту α=20°, и при угле β=20°. Она может стать на 40—50% больше нагрузки по нормали к плоскости фермы.

Ветровая нагрузка на пространственные решетчатые конструкции исследована главным образом для четырехгранных и трехгранных башен и мачт с оттяжками, т. е. конструкций с большим удлинением. Балки жесткости висячих мостов, мосты перегружателей, эстакады имеют ту же особенность, что не позволяет вводить в расчеты понижающий коэффициент, зависящий от удлинения.

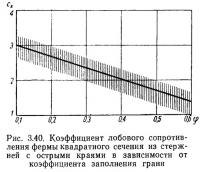
Выяснение ветровой нагрузки на башни и мачты проводилось на моделях всей конструкции или ее секций. Исследованиями моделей квадратного сечения решетчатых конструкций из угловой стали установлено: чем меньше коэффициент заполнения фермы (грани), тем больше коэффициент лобового сопротивления (рис. 3.40). Штриховкой показана область разброса опытных данных по различным конструкциям.

По СНиП коэффициент лобового сопротивления решетчатой пространственной конструкции квадратного сечения при ветре, нормальном к плоскости фермы,


где с_ф — коэффициент лобового сопротивления плоской фермы;
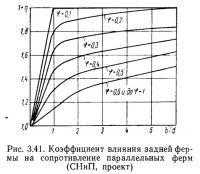
η — коэффициент влияния задней фермы по рис. 3.41.

Коэффициент лобового сопротивления плоской фермы с_ф определяется по формуле (3.16) или (3.17). Здесь обозначения взяты по СНиП.

Для трехгранной башни при коэффициенте заполнения фермы φ≥0,1 коэффициент с_пр согласно СНиП умножается на 0,9; разное направление ветра на конструкцию не учитывается.

При ветре по диагонали квадратной решетчатой башни коэффициент спр, вычисленный по формуле (3.19), умножается на коэффициент φ, принимаемый равным:

• для стальных башен из одиночных уголков — 1,1
• то же, из составных элементов, железобетонных башен и деревянных башен из одиночных элементов — 1,2
• для деревянных башен из составных элементов — 1,3

Опытные данные, полученные на моделях отсеков конструкций с малым коэффициентом заполнения, характерным для строительства последних лет, свидетельствуют о необходимости повышения аэродинамических коэффициентов. К таким сооружениям относятся башни с гибкими раскосами, когда основной наветренной площадью становятся пояса. В известной мере это относится и к мачтам, решетка которых выполнена из двух перекрещивающихся раскосов из круглой стали, что делают для снижения ветровой нагрузки.

Обычно наибольшая нагрузка бывает при ветре, направленном на угол решетчатой башни квадратного сечения — по диагонали. В ряде случаев наибольшее давление на нее может быть при ином направлении ветра, например под углом 30°.

На рис. 3.42 приведены коэффициенты лобового сопротивления квадратного сечения решетчатой конструкции, выполненной из круглой стали с шероховатостью ее поверхности k/d = = 1·10^—3 (k=40 мк). Модели исследовались при числе Re=118000, отнесенном к диаметру пояса фермы (В. И. Ханжонков). Кризис у таких шероховатых стержней наступает раньше — при Re=(0,5÷2)·10⁵. Наибольшее значение с_х конструкции наблюдается при угле α=20÷30°, а не при 45°, как это наиболее часто у ферм из угловой стали. Давление на пространственную, конструкцию из круглых стержней примерно в 2,1 раза больше давления на ее грань. Это относится к раскосным и безраскосным конструкциям с коэффициентом заполнения грани 0,18—0,24 и. с различными узловыми соединениями.

Исследование моделей четырехгранных решетчатых призм из круглой стали, на которых были установлены секции телевизионных антенн, выполненные из труб, выявили аналогичное поведение конструкций (МГУ). Зависимость коэффициента лобового сопротивления от чисел Рейнольдса Re= (5÷10)·10⁴, вычисленных по диаметру поясов модели, не обнаружена. Наибольшее значение коэффициента с_х наблюдается также при угле α=20—30°, а не при α=45°. Коэффициент с_х квадратного сечения решетчатых призм на 20—30% больше коэффициента с_х одиночного круглого цилиндра. Степень турбулентности аэродинамической трубы, где проводились эти измерения, ε=0,1%; она определена по шару (Re=375000) известным способом.

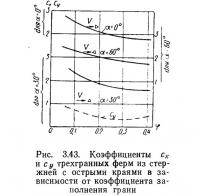
Преимущества трех поясов в сечении вызвали появление трехгранных башен и мачт. Наибольшая ветровая нагрузка на трехгранную решетчатую призму будет при ветре по нормали к грани, потому что в этом случае затенение задних стержней наименьшее (рис. 3.43). При ветре по биссектрисе угла и ветре, направленном параллельно одной из граней конструкции, нагрузка будет меньше, чем при направлении ветра на грань. Характерна значительная подъемная сила при углах атаки а = 30°, что учитывают в расчетах. Эти данные относятся к конструкциям из стержней с острыми краями (см. табл. 3.1).

Коэффициент лобового сопротивления трехгранных ферм из круглой стали, подобных четырехгранным, в условиях докризисного обтекания (Re=1,18·10⁵) увеличивается примерно в 1,6 раза по сравнению с сопротивлением плоской фермы той же конструкции (рис. 3.44). Коэффициент заполнения грани этих ферм 0,18—0,24. Наибольшая величина коэффициента лобового сопротивления фермы остается примерно постоянной в пределах углов α=0—15° и α=45—60°, минимум коэффициента с_х наблюдается вблизи угла а = 30°, но в окрестности этого угла появляется значительная подъемная сила.

Ветровую нагрузку на решетчатые конструкции из труб или круглых стержней определяют по формуле (3.15). При осреднении числа Рейнольдса по диаметру стержней фермы искажается представление о действительной картине обтекания: если число Рейнольдса вычислено по большому диаметру поясов, то обтекание решетки окажется также закризисным; на самом деле для меньшего диаметра решетки оно будет докризисное. Для таких конструкций тем более недопустимо относить число Рейнольдса к размеру поперечного сечения всей фермы.

Ветровую нагрузку на пространственную конструкцию с шестью гранями и более определяют, рассматривая ее состоящей из двух половин решетчатого многогранника. Нагрузку на наветренную ферму определяют как на условную плоскую ферму, являющуюся проекцией ферм на плоскость симметрии конструкции, т. е. учитывают углы наклона (скольжения) отдельных граней. При этом принимают во внимание удлинение граней, форму сечения стержней, коэффициент заполнения и число Рейнольдса — для круглых стержней. За расстояние между этими условными фермами принимают диаметр окружности, вписанной в многоугольник. Подветренную ферму учитывают коэффициентом η. Расчетным случаем будет часто ветер, направленный па нормали к плоскости одной из граней, если конструкция — с четным числом граней, что встречается чаще.

Ветровую нагрузку на многогранную решетчатую конструкцию определяют, пользуясь данными о коэффициентах лобового сопротивления фермы при различных углах скольжения (см. рис. 3.34 и 3.39), Елияние подветренных ферм учитывают коэффициентом, например, по рис. 3.41.

При размещении на опоре технологического оборудования расчетной схемой будет наиболее неблагоприятное сочетание нагрузок на несущую конструкцию и оборудование, принимая при каждом направлении ветра свой коэффициенты лобового сопротивления, т. е. с учетом углов атаки и скольжения.

Коэффициент лобового сопротивления n одинаковых плоских решетчатых ферм, расположенных параллельно и на равном расстоянии друг от друга, определяют по формуле


где с^ф_х — коэффициент лобового сопротивления одинарной фермы, в котором учтены особенности формы сечения и размеры стержней;
η — принимается по рис. 3.41.

Расчетная ветровая нагрузка на пространственную конструкцию из многих параллельных ферм будет при направлении ветра под небольшими углами. Она на 10—20% больше, чем нагрузка по формуле (3.20).

Для определения ветровой нагрузки на пространственные решетчатые конструкции предложены различные формулы, в которых в том или ином виде участвует коэффициент заполнения. Распространена формула


в которой постоянные a и b зависят от профиля стержней фермы, формы сечения пространственной конструкции (треугольная, квадратная или иная), соотношения высоты фермы к ее длине и коэффициента заполнения φ.

Формулы вида

или

как и более сложные, являются по существу приближенным аналитическим выражением экспериментальной зависимости, т. е. справедливы, строго говоря, для определенного вида исследованных конструкций.

Постоянная а в формуле (3.21) чаще всего назначается несколько больше среднего коэффициента лобового сопротивления двух ферм при бесконечно большом расстоянии между ними. В ней учитывают и число граней конструкции. Например, в Чехословакии в нормах проектирования антенных сооружений для решетчатых конструкций из стержней с острыми краями рекомендуются следующие постоянные:


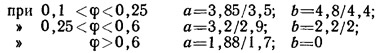
Здесь в числителе приведены значения постоянных для квадратного сечения и прямоугольного с отношением сторон 1:2, в знаменателе — для треугольного сечения. Для конструкций из трубчатых или круглых элементов приведенные выше значения умножаются на коэффициент 0,75; при этом подразумевается докризисное обтекание стержней.

Исследования моделей квадратного сечения решетчатых ферм из угольников и труб показали, что их сопротивление, рассчитанное по этим нормам, больше действительного на 18—27% (первая цифра относится к конструкциям из угловой стали, вторая — из труб). Превышение рассчитанного сопротивления треугольных конструкций из труб — 5—27%. Коэффициент заполнения опытных ферм 0,185. Для плоских решетчатых ферм нормы дают превышение всего лишь на 8—18%. Скорость потока в опытах была до 30 м/сек, что свидетельствует о докризисном обтекании круглых цилиндров.

Действие ветра на угол — по диагонали — четырехгранной конструкции учитывают иногда коэффициентом 1—0,6φ. Нагрузку на трехгранную решетчатую конструкцию чаще всего принимают не зависящей от направления ветра. Это следует и по СНиП.

Для высотных сооружений типа радиомачт, башен различного назначения, телевизионных опор, а также больших радиотелескопов, ветровая нагрузка на которые является доминирующей над остальными, пользование осредненными коэффициентами лобового сопротивления, рекомендуемыми нормативами для промышленного строительства, может дать ошибочное представление о величине ветровой нагрузки. Это обстоятельство заставило исследовать модели высотных сооружений или вводить повышенное значение коэффициентов лобового сопротивления, что делают чаще.

Коэффициент лобового сопротивления обычных плоских решетчатых ферм из стержней с острыми краями, равный 1,4, для высоких сооружений с большими панелями, т. е. с малым коэффициентом заполнения фермы, надо считать заниженным. В большинстве стран наименьшее значение коэффициента лобового сопротивления таких ферм равно 1,6.

В США, например, приняты следующие величины коэффициентов лобового сопротивления решетчатых башен из стержней с острыми краями (угольники, швеллеры и др.): для четырехгранных конструкций при действии ветра по нормали к плоскости грани — 2,2/1,7; на угол 2,4/1,9; для трехгранных по нормали к грани — 2,1/1,6, параллельно грани — 1,6/1,3. Здесь в числителе дано значение с_х при коэффициенте заполнения фермы φ=0,14, а в знаменателе — при φ=0,27. Величина сопротивления решетчатых конструкций из труб или круглых элементов уменьшается умножением на коэффициент 0,67, полагая докризисное обтекание. В этих нормах средний коэффициент лобового сопротивления пространственных конструкций из элементов с острыми краями при действии ветра нормально к одной из четырех граней — 2,2, при действии на угол — 2,4, на трехгранную конструкцию: нормально к грани — 2,0, параллельно грани — 1,5.

Влияние второй (задней) фермы учитывают коэффициентом 1,6, принимая усредненное значение коэффициента лобового сопротивления, равное 1,7. Вообще говоря, значение с_х может быть 1,5—1,8.